חלק מהשלם – 3/5 חלק א

הרשמה

רכישה

חלק מהשלם – 3/5 חלק א

- כל תלמיד יבחר נייר אחד גדול ונייר אחד קטן.
- כל תלמיד יקבל שני ניירות 15ס”מ/ 15ס”מ ונייר נוסף בגודל 7.5ס”מ/ 7.5ס”מ.
- הניחו לפניכם: נייר אחד גדול ונייר אחד קטן.
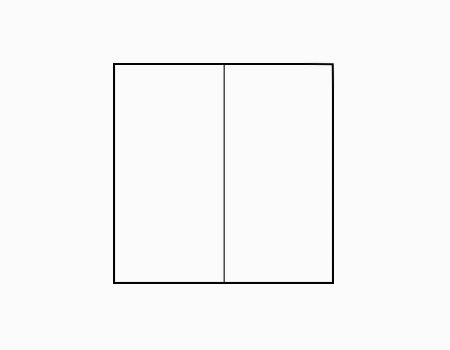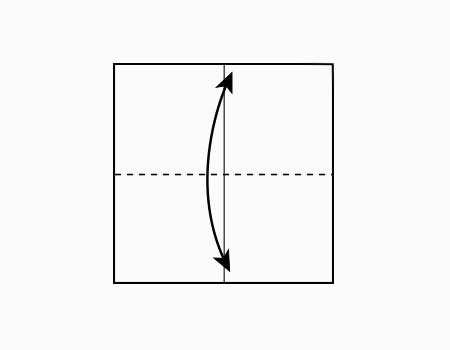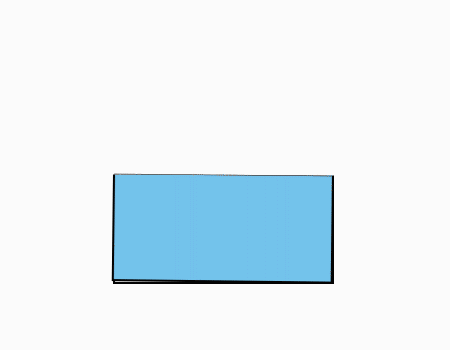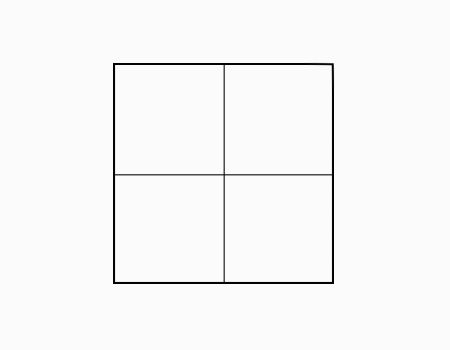
- הוראת קיפול: לקפל ב- 2 הניירות צלע לצלע מקבילה ולפתוח.
- נקפל בכל הניירות.
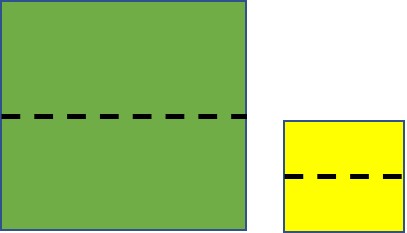
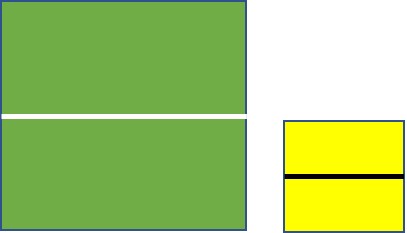
- משימה: הניחו על השולחן ריבוע אחד גדול וריבוע אחד קטן כמו באיור.
- שאלה לדיון: האם נוכל לומר שגודל שטחו של כל מלבן שהתקבל לאחר הקיפול הוא חצי משטחו של הריבוע ? האם זה נכון גם בדף הגדול וגם בדף הקטן? הסבירו
- להדגיש כל הזמן שהמכנה בשבר 1/2 מציין מספר חלקים שווים בשטחם חולק הנייר. כך זה בכל שבר ללא התייחסות למונה. לאחר שקבענו את החצי הוא יהיה שלם חדש בפני עצמו והמונה יציין כמה שלמים כאלו לוקחים ביחד. אם נקח יותר מ- 2 יהיה לנו שבר גדול מ-1.
- תשובה: גם בנייר הגדול וגם בנייר הקטן, צורת המלבן היא חציו של השלם. (השלם הוא הנייר בצורת ריבוע).
- כשאומרים חצי הכוונה לחצי ביחס לשלם נתון. כי יתכן שחצי אחד אינו שווה לחצי אחר במקרה שלנו כאשר מציגים שני דפים (שלמים) בגדלים שונים.
- הוראת קיפול: לקפל בכל הניירות צלע לצלע מקבילה ולפתוח,כך שיתקבלו בכל נייר 4 ריבועים.
- משימה: סמנו עם המודד בשני הניירות את קווי הקיפול שהתקבלו לאחר הקיפול.
- שאלה לדיון: בחנו את ארבעת הריבועים שנוצרו אחרי הקיפול איזה חלק מתוך הריבוע השלם כל ריבוע קטן? הסבירו
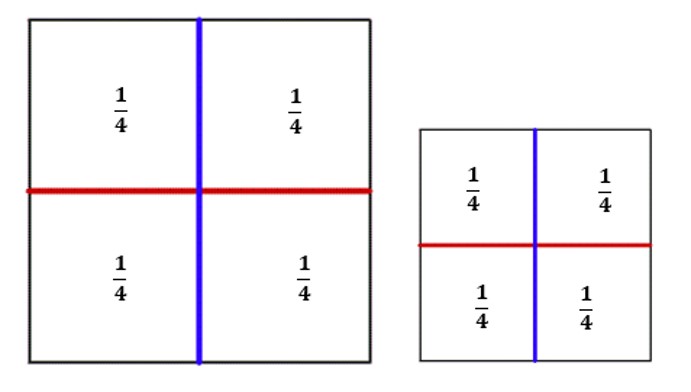
- במקרה הזה כל הריבועים הקטנים חופפים. גודל שטחו של כל ריבוע קטן הוא רבע משטחו של הריבוע הגדול. בהמשך נראה מצבים בהם הרבעים המסומנים אינם חופפים אך גודל שטחם הוא שווה.
- תשובה 1: בכל אחד מהניירות שטחו של הריבוע הקטן (בנייר הגדול והקטן) הוא רבע מגודל שטחו של הריבוע הגדול.
- תשובה 2: נוכל לסמן כל רבע עם השבר היסודי $\dpi{120} \bg_white \frac{1}{4}$ יש 4 ריבועים שווה שטח בכל אחד מהניירות שקיפלנו.
- הוראת קיפול: לקפל רק בנייר הגדול כל צלע לקו הסימטריה ולפתוח, כפי שמודגם באנימציה.
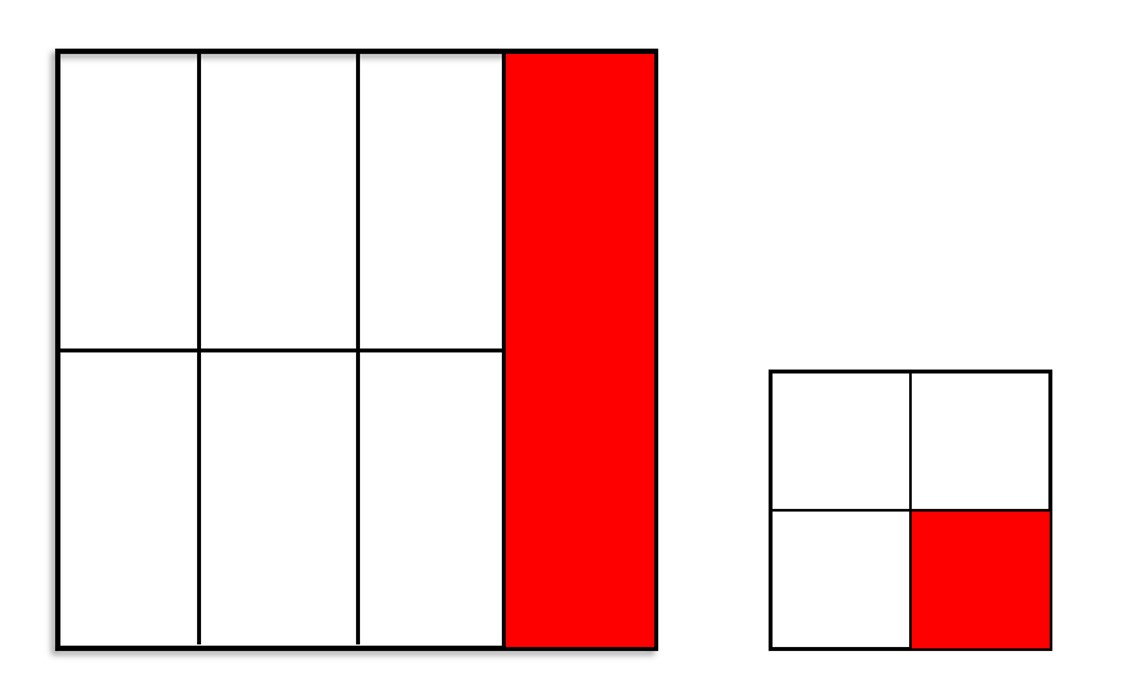
- שאלה לדיון: איזה חלק של הניירות הוא המצולע המסומן באדום?הסבירו
- כאן המקום לציין שכל מצולע אדום (בפרט שאינם חופפים) מיצג גודל שטח של רבע. אבל הוא רבע ביחס לשלם. במקרה שלפנינו השלמים אינם שווים בגודל שטחם.
- תשובה: המצולע המסומן באדום הוא רבע משטחו של כל אחד מהניירות המקופלים. והוא מיוצג על ידי השבר היסודי $\dpi{120} \bg_white \frac{1}{4}$ .
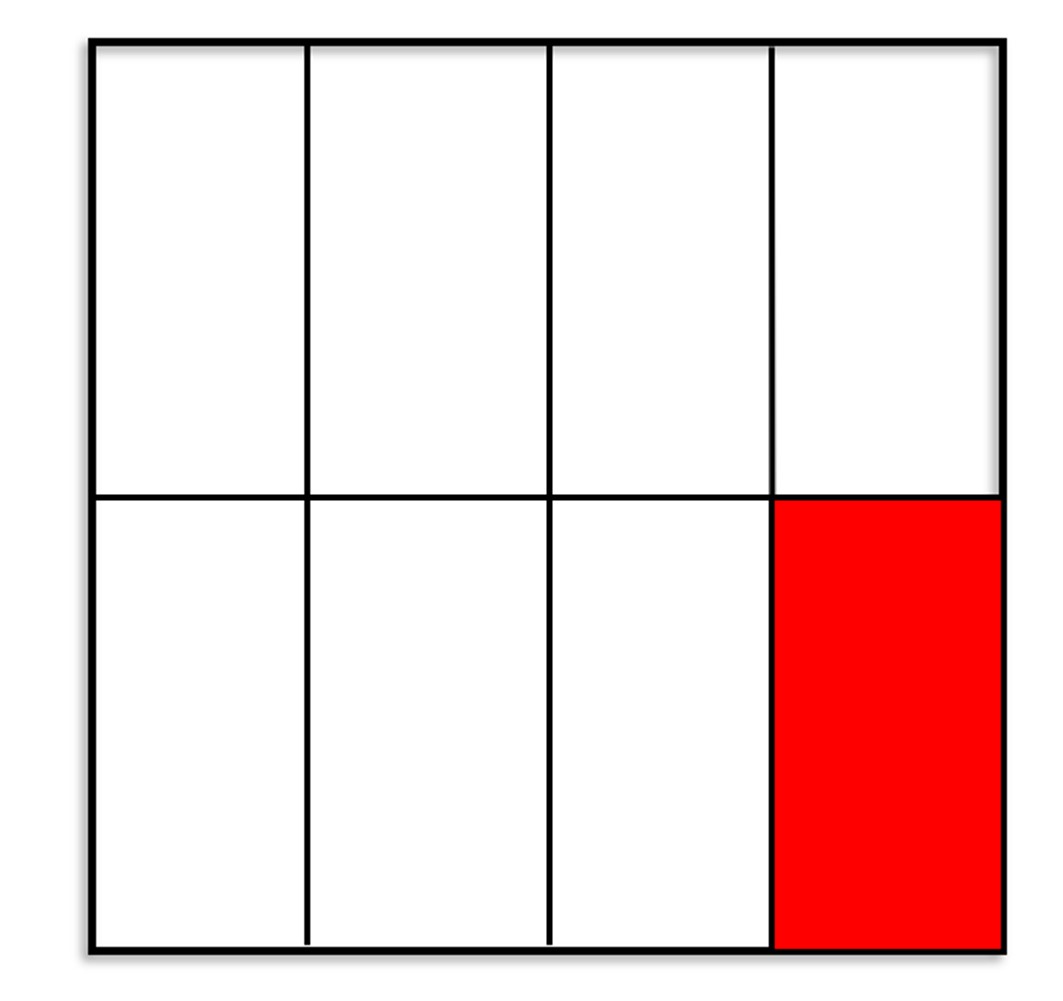
- מאחר שכל מלבן בנייר הגדול הוא 1/8 האדום ייצג 2/8 של הנייר הגדול
- שאלה לדיון: האם שני המרובעים המסומנים באדום שווים בשטחם?הסבירו.
- תשובה: גודל שטחם של שני המרובעים האדומים אינם שווים בשטחם מאחר שכל נייר מקופל אינו באותו גודל.
- שאלה לדיון: איזה חלק בנייר הגדול הוא מלבן המסומן באדום? איזה שבר יסודי מציין את החלק של כל אחד מהמלבנים? הסבירו.
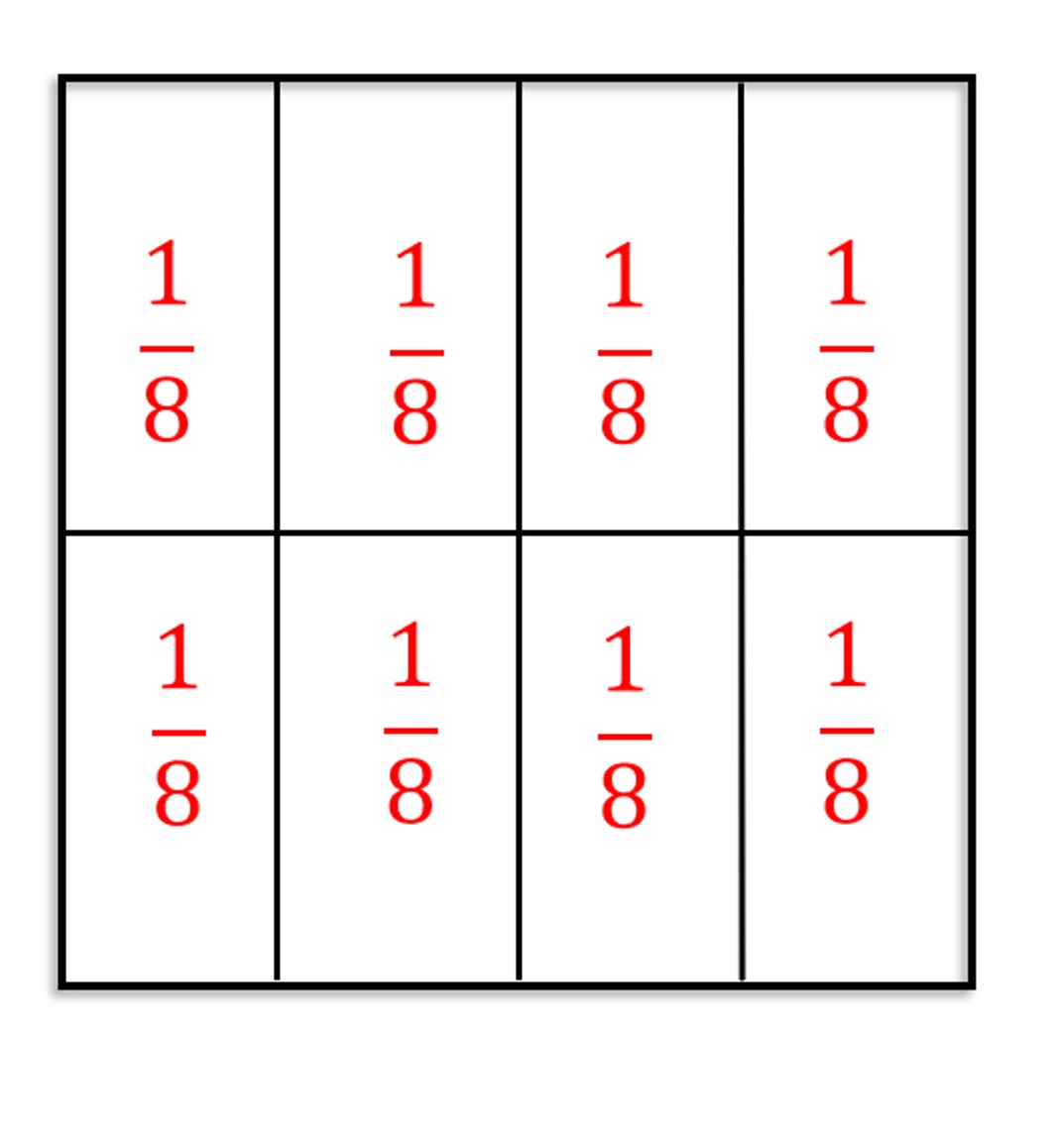
- תשובה :בכל נייר מקופל יש 8 מלבנים והם שווים בשטחם. נוכל לסמן כל שמינית עם השבר היסודי $\dpi{120} \bg_white \frac{1}{8}$ .
- הוראת קיפול: כל תלמיד יקבל את דפי העבודה המצורפים לשיעור.
- בשלב זה מומלץ לחלק לכל תלמיד דפי עבודה המצורפים לשיעור.
- משימה אישית :צבעו בדף העבודה $\dpi{120} \bg_white \bg_white \large \frac{4}{8}$ וכיתבו מהו השם שתתנו לחלק שצבעתם?
- בשלב זה כדאי לחלק לתלמידים דף עבודה המצורף לשיעור.
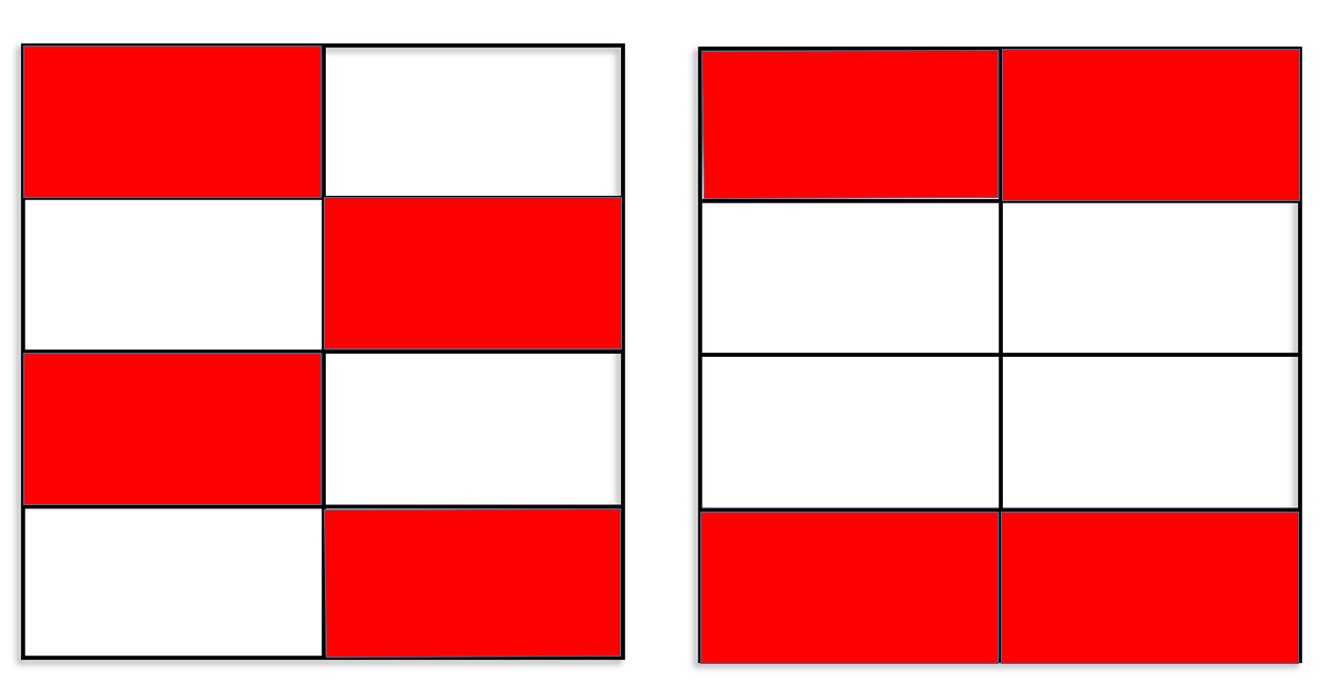
- תשובה: בשני האיורים מוצגים 4 מלבנים צבועים מתוך 8 מלבנים. ניתן ליצג כל איור על ידי השבר $\dpi{120} \bg_white \large \frac{1}{2}$ וגם על ידי $\dpi{120} \bg_white \large \frac{2}{4}$ .
- לפתח שיחה עם הילדים שיסבירן בדרכים שונות את השוויונות 1/2=2/4=4/8.בשעורים קודמים הכירו 1/4 וגם 1/2
- תשובה: בשני האיורים מוצגים 4 מלבנים צבועים מתוך 8 מלבנים. ניתן ליצג כל איור על ידי השבר $\dpi{120} \bg_white \bg_white \large \frac{1}{2}$ וגם על ידי $\dpi{120} \bg_white \bg_white \large \frac{2}{4}$ .
- משימה אישית :צבעו בדף העבודה $\dpi{120} \bg_white \bg_white \large \frac{6}{8}$ וכיתבו מהו השם שתתנו לחלק שצבעתם?
- תעודדו את התלמידים לצבוע את החלק 6/8 בדרכים שונות. רצוי לקחת ניירות נוספים, לקפל לשמיניות ותלמידים יציגו דרכים שונות לצביעה
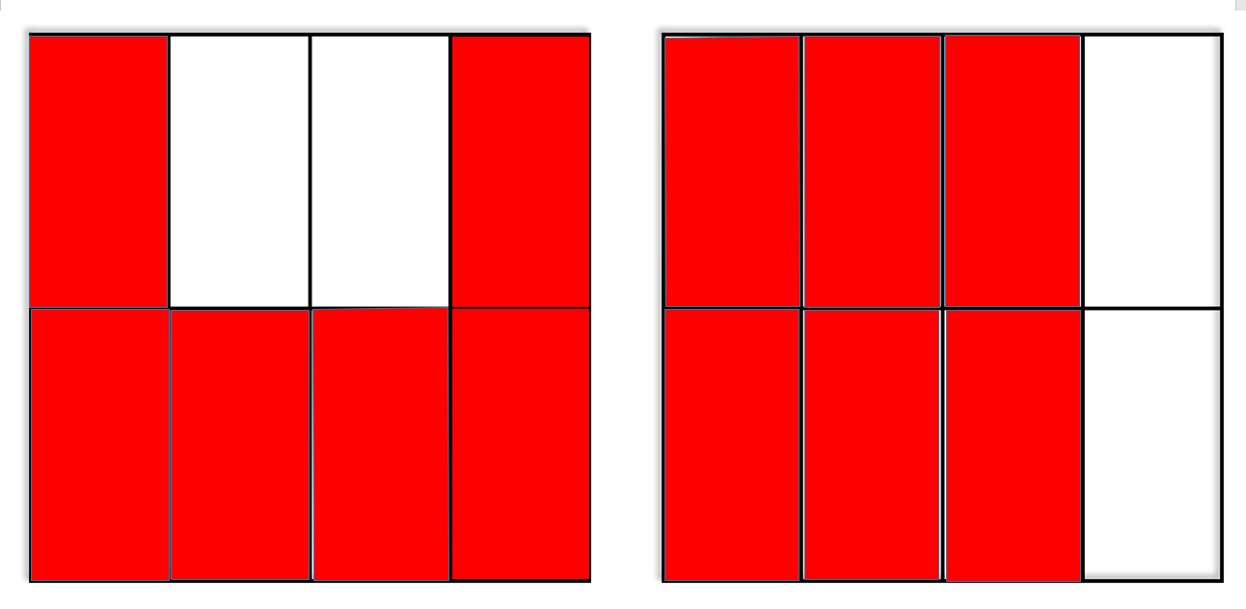
- תשובה: מוצגים שתי אפשרויות לצבוע $\dpi{120} \bg_white \bg_white \large \frac{6}{8}$ החלק $\dpi{120} \bg_white \bg_white \large \frac{6}{8}$ ניתן לייצג על ידי השבר $\dpi{120} \bg_white \bg_white \large \frac{3}{4}$ .
- לפתח שיחה עם הילדים שיסבירו בדרכים שונות את השוויון 3/4=6/8.בשעורים קודמים הכירו 3/4 וגם 3/8 .יש להדגיש שהמונה והמכנה 3 ו-4 בשבר 3/4 הם מספרים זרים(גורם משותף היחיד הוא 1) ולכן לא ניתן לרשום שבר שווה ערך ל 3/4 עם מכנה ומונה קטן יותר.
- משימת סיכום: בכל אחד מהריבועים צבעו אחד השברים מהסדרה $\dpi{120} \bg_white \bg_white \large \frac{1}{8}$ עד $\dpi{120} \bg_white \bg_white \large \frac{8}{8}$ ורשמו על יד כל ריבוע גודל החלק הצבוע.
- על התלמידים להכיר את הסדרה העולה של התשיעיות כאשר כל המכנים הם 8 (1/8,2/8,3/8
  ,4/8,5/8,6/8,7/8,8/8)
  וגם הסדרה (1/8,1/4
  ,3/8,1/2,5/8,3/4,7/8,1)

מטרת הפעילות
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.

שם הדגם
ללא דגם

בשיעור זה התלמידים יכינו את הקיפולים. ובשיעור הבא יקפלו מהם הדגם של עץ.

מספר סידורי: 4052/1

שם היוצר/ת
פול ג’קסון

© כל הזכויות שמורות למרכז הישראלי לאוריגאמי

רצף מומלץ
מומלץ ללמד לפי הרצף המופיע באתר (בהתאם לתכנית הלימודים).

על השיעור
שיעור 3/5 חלק א.

התלמידים יקפלו 2 ניירות בגדלים שונים כשנייר אחד הוא רבע מהנייר הגדול. בכל שלב התלמידים יחקרו את החלקים מתוך השלם.

התלמידים יכירו את השברים עם מכני 2,4,8 ושמות שונים לאותם שברים.

לשיעור מוצמדים דפי משימות לתרגול נושא השברים- מומלץ להדפיס ולחלק לתלמידים לקראת השיעור.

ציוני דרך
כיתה ד – עמוד 1

מילון מונחים בגאומטריה

הדגשים בהוראת השבר כחלק משלם:
1. קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
2. החלקים לא חייבים להיות חופפים.
3. כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
4. חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
5. כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
6. השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול יותר משטחו של שלושה רבעים של ריבוע קטן.

משוב מעמיתים

שדה חובה*

You must be logged in to post a comment.

חלק מהשלם – 3/5 חלק א

משוב מעמיתים

שיעורים

אודות

צור קשר