כיתה ד
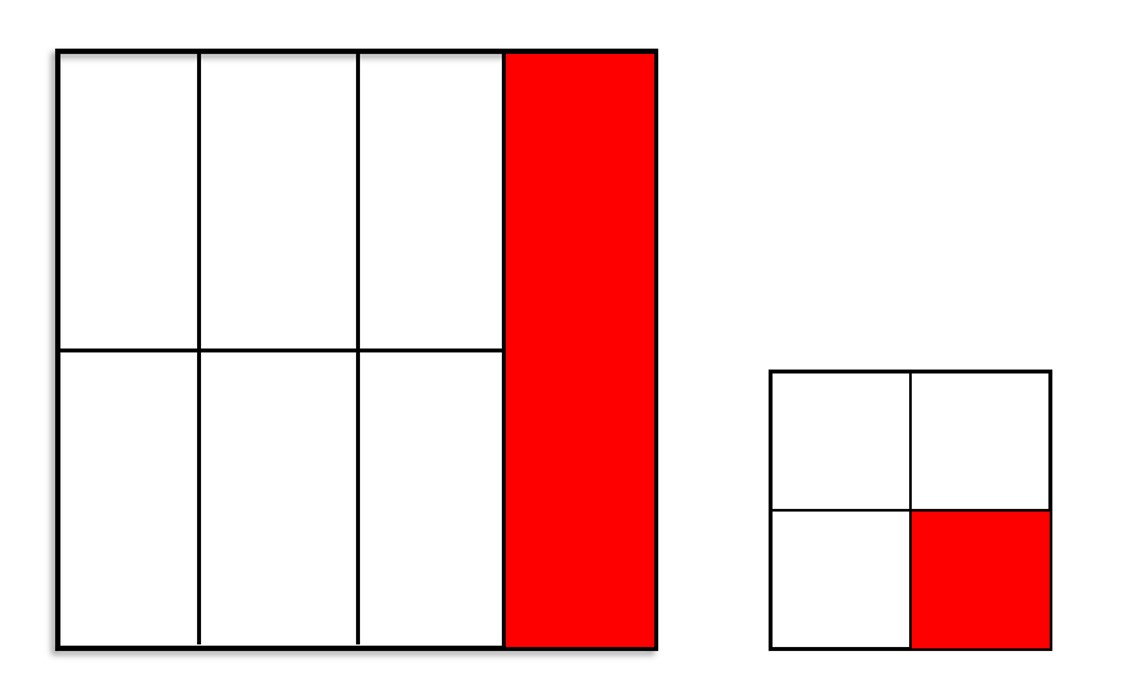
חלק מהשלם 2/5 חלק א
- מטרת הפעילות
- הכרת השברים היסודיים 1/3,1/9 באמצעות מודל השטח.
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- זיהו ורישום חלקי השלם במודל השטח ולא רק שברים יסודיים (המונה אינו 1)
- שם הדגם
הכנה למשחק גלגלון \ דומינו ראלי
מספר סידורי 3025
- על השיעור
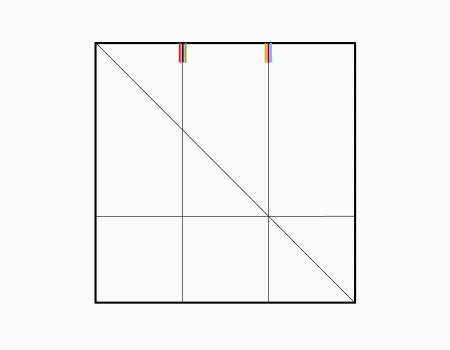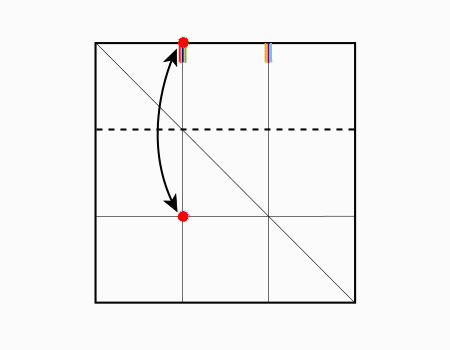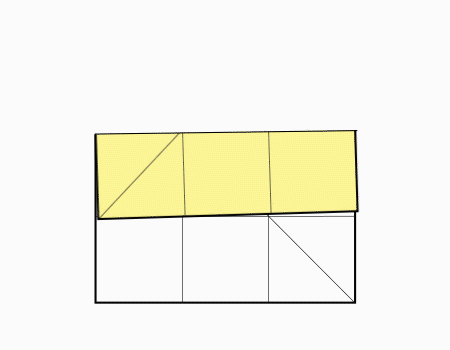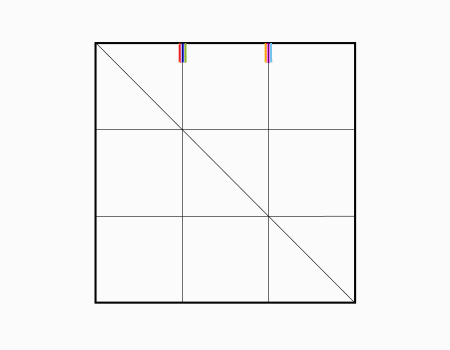
על ידי קיפול התלמידים מכירים השברים היסודיים,1/9 1/3 כחלק של שלם
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ציוני דרך
-
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול משטחו של שלושה רבעים של ריבוע קטן.
- חומרים
בפעילות זו נמשיך לקפל מהניירות שהשתמשנו בהם בשיעור קודם.
חלק מהשלם 2/5 חלק ב
- מטרת הפעילות
- הכרת השברים היסודיים 1/3,1/9 באמצעות מודל השטח.
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- זיהו ורישום חלקי השלם במודל השטח ולא רק שברים יסודיים (המונה אינו 1)
- שם הדגם
הכנה למשחק גלגלון \ דומינו ראלי
מספר סידורי 3025
- על השיעור
על ידי קיפול התלמידים מכירים השברים היסודיים,1/9 1/3 כחלק של שלם
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ציוני דרך
-
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול משטחו של שלושה רבעים של ריבוע קטן.
- חומרים
בפעילות זו נמשיך לקפל מהניירות שהשתמשנו בהם בשיעור קודם.
חלק מהשלם 2/5 חלק ג
- מטרת הפעילות
- הכרת השברים היסודיים 1/3,1/9 באמצעות מודל השטח.
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- זיהו ורישום חלקי השלם במודל השטח ולא רק שברים יסודיים (המונה אינו 1)
- שם הדגם
משחק גלגלון \ דומינו ראלי
מספר סידורי 3025
- על השיעור
על ידי קיפול התלמידים מכירים השברים היסודיים,1/9 1/3 כחלק של שלם
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ציוני דרך
-
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול משטחו של שלושה רבעים של ריבוע קטן.
- חומרים
בפעילות זו נמשיך לקפל מהניירות שהשתמשנו בהם בשיעור קודם.
חלק מהשלם – 3/5 חלק א
- מטרת הפעילות
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- שם הדגם
ללא דגם
בשיעור זה התלמידים יכינו את הקיפולים. ובשיעור הבא יקפלו מהם הדגם של עץ.
מספר סידורי: 4052/1
- על השיעור
שיעור 3/5 חלק א.
התלמידים יקפלו 2 ניירות בגדלים שונים כשנייר אחד הוא רבע מהנייר הגדול. בכל שלב התלמידים יחקרו את החלקים מתוך השלם.
התלמידים יכירו את השברים עם מכני 2,4,8 ושמות שונים לאותם שברים.
לשיעור מוצמדים דפי משימות לתרגול נושא השברים- מומלץ להדפיס ולחלק לתלמידים לקראת השיעור.
- ציוני דרך
-
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול יותר משטחו של שלושה רבעים של ריבוע קטן.
חלק מהשלם – 3/5 חלק ב
- מטרת הפעילות
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- שם הדגם
ללא דגם
מספר סידורי: 4052/2
- על השיעור
שעור 3/5 חלק ב.
בשיעור זה עוסקים גם במכנים 2,4,8,16 ושמות שונים אבל הדגש הוא על הגורם המשותף הגדול ביותר של המונה והמכנה. השם המתאים לשבר הוא כאשר אין גורם משותף למונה ומכנה פרט ל 1.
- ציוני דרך
-
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול יותר משטחו של שלושה רבעים של ריבוע קטן.
חלק מהשלם – 3/5 חלק ג
- מטרת הפעילות
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- שם הדגם
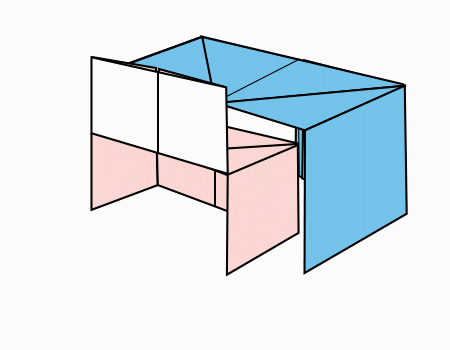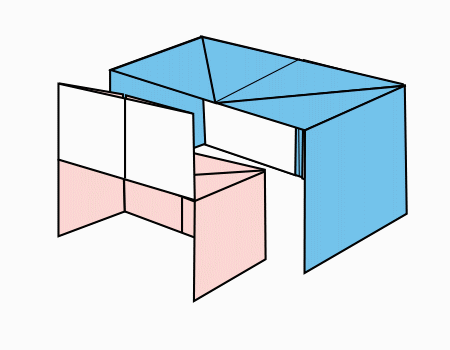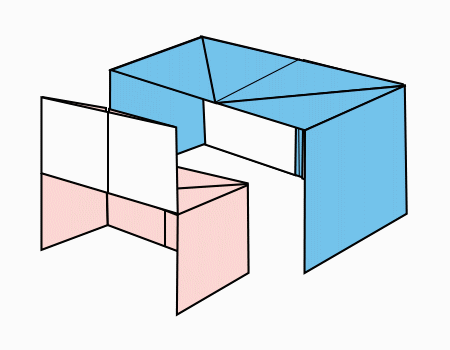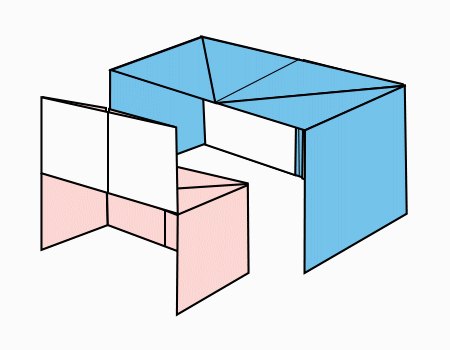
שולחן תלמיד וספסל
בשיעור זה התלמידים יכינו את הקיפולים. ובשיעור הבא יקפלו מהם הדגם של עץ.
מספר סידורי: 4052/3
- על השיעור
שיעור 3/5 חלק ג
התלמידים יקפלו 2 דפים בגדלים זהים ודף אחד שהוא רבע מהדפים הגדולים. בכל שלב יחקרו את החלקים מתוך השלם.
כאן הדגש בהכרת חלוקה שווה לחלקים שאינם חופפים ובכל זאת שווה שטח.
- ציוני דרך
-
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול יותר משטחו של שלושה רבעים של ריבוע קטן.
חלק מהשלם 4/5
- מטרת הפעילות
- הכרת שברים פשוטים עם מכנים 2,4,8,16
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- זיהו ורישום חלקי השלם במודל השטח ולא רק שברים יסודיים (המונה אינו 1)
- שם הדגם
מניפה
מספר סידורי 4053
- על השיעור
השיעור עוסק במערכות השברים n/2,n/4,n/8,n/16 ושמות שונים לשברים
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ציוני דרך
כיתה ד
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול משטחו של שלושה רבעים של ריבוע קטן.
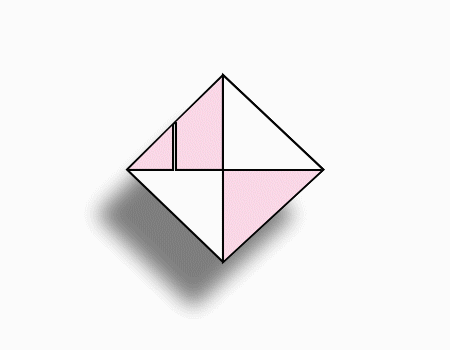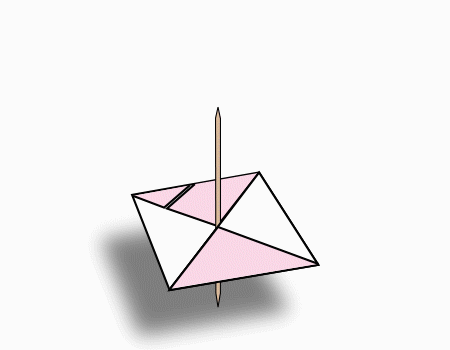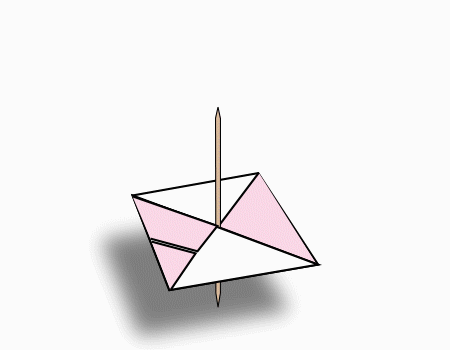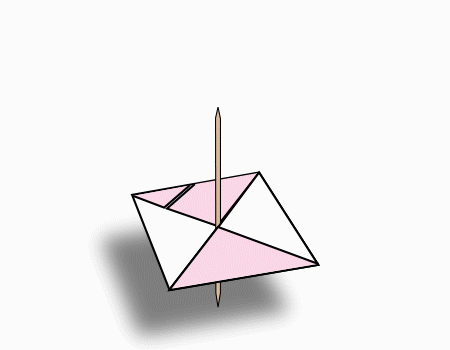
חקר מצולעים – סביבון
- מטרות השיעור
התלמידים יזהו ויחקרו את תכונות המצולעים.
התלמידים יחשבו את סכום הזוויות במחומש ובמשושה.
- שם הדגם
סביבון
מספר סידורי:4056
- יוצר/ת הדגם
פול ג’קסון
© כל הזכויות שמורות למרכז הישראלי לאוריגאמי
- רצף מומלץ
מומלץ ללמד לפי הרצף המופיע באתר (הרצף על פי תכנית הלימודים).
- על השיעור
בפעילות התלמידים יחקרו את המרובעים ויחשבו את סכום הזוויות במשחומש ובמשושה. בסוף הפעילות יתקבל סביבון.
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ידע נדרש
הכרה וחישוב זוויות.
- חומרים
- נייר אוריגאמי לכל תלמיד בגודל 15/15 ס”מ, וקיסמים (קיסם שיניים)
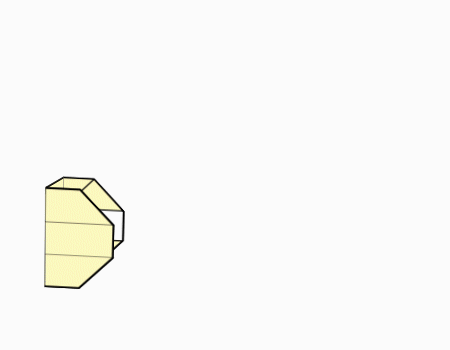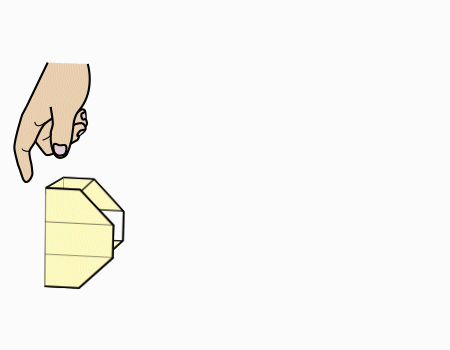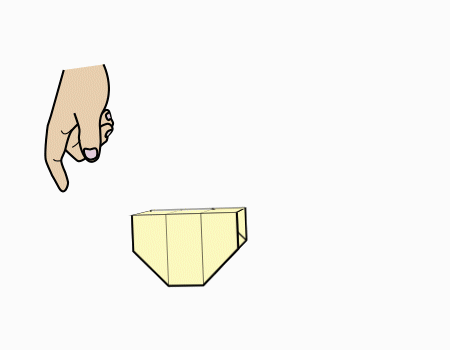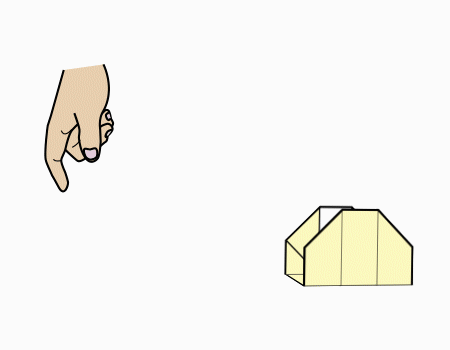
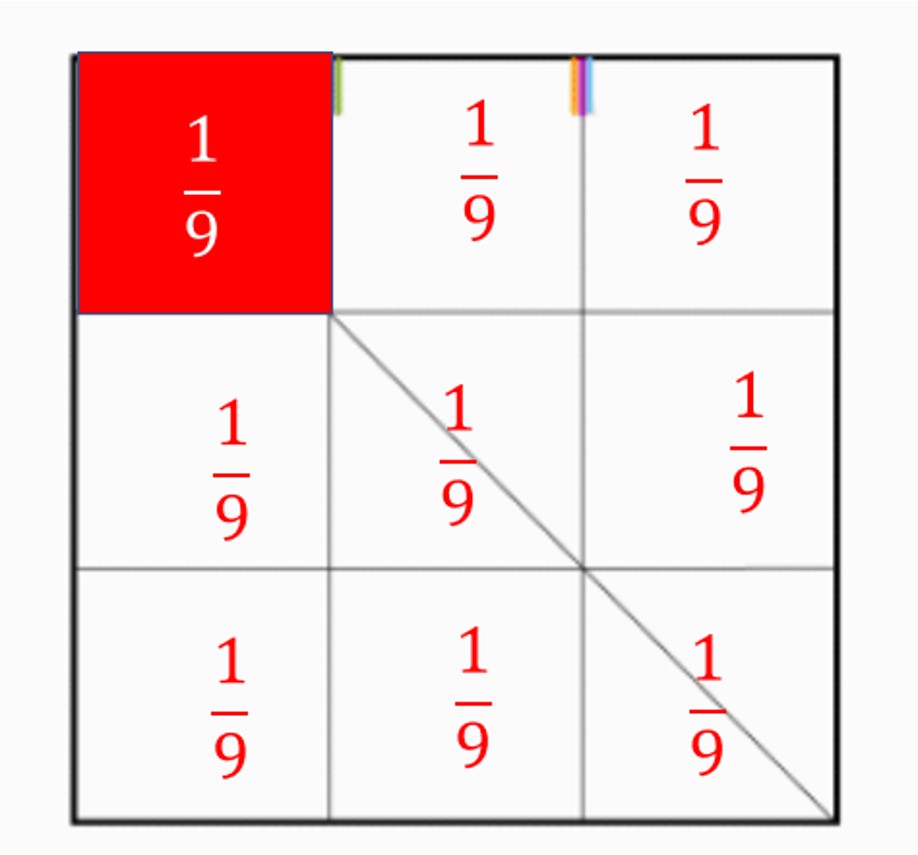
חלק מהשלם 5/5
- מטרת הפעילות
- הכרת השברים היסודיים באמצעות מודל השטח.
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- זיהו ורישום חלקי השלם במודל השטח ולא רק שברים יסודיים (המונה אינו 1)
- שם הדגם
ללא דגם
מספר סידורי 4054
- על השיעור
השיעור עוסק במערכות השברים n/3,n/9 ושמות שונים לשברים.
השיעור משמש כהכנה לשיעור המשך העוסק במערכות שברים n/18,n/36.
.
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ציוני דרך
כיתה ד –
הדגשים בהוראת השבר כחלק משלם:
- קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
- החלקים לא חייבים להיות חופפים.
- כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
- חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
- כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
- השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול משטחו של שלושה רבעים של ריבוע קטן.
קרנבל מצולעים
- מטרת הפעילות
התלמידים בוחנים מצולעים לפי מספר הצלעות, קו סימטריה שיקופית ומצולע קמור וקעור.
- שם הדגם
מסכה לפורים
מספר סידורי 3000/2
- רצף מומלץ
מומלץ ללמד לפי הרצף המופיע באתר (הרצף על פי תכנית הלימודים)
- על השיעור
- השיעור מתמקד בנושא של מצולעים לפי מספר הצלעות.
- כמו כן יש התייחסות למצולעים קמורים ולא קמורים.
- יש התייחסות לקווי סימטריה שיקופית
משך זמן הפעילות המומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ידע נדרש
מצולעים קמורים וקעורים(או שאינם קמורים)
הגדרות פורמליות
- מצולע קמור-מצולע שכל אלכסוניו מוכלים בו.
- מצולע קמור-מצולע שכל אחת מהזוויות הפנימיות שלו קטנה -מ 180ᵒ
- מצולע קמור-מצולע שבו כל קטע המחבר שתי נקודות כלשהן של המצולע נמצא בתוך המצולע או על שפתו
הערה: ההגדרה הראשונה הנשענת על אלכסונים היא הקלה ביותר לבדיקה.
ההגדרה השלישית ניתן לסביר בצורה אינטואיטיבית מגיל הגן באופן הבא: מעמידים (או מסמנים) שני ילדים בתוך המצולע (או ילד אחד או שניים על שפתו של המצולע). הילדים מותחים חבל או חוט ביניהם. קו הישר של החבל תמיד יהיה בתוך המצולע (או על שפת המצולע)מצולע קעור (או עדיף לומר שאינו קמור)
לפי ההסבר האחרון של קמור יתכן מצב שהקו המחבר בין שני ילדים יוצא מתחום המצולע. בגן השתמשנו בגומי גדול ומשכנו את הגומי לקבל מצולע קעור. העמדנו שני ילדים וזרקו כדור אחד לשני וראו שהכדור יצא מתחום הגומי (או מקל מטאטא).