קו השיקוף במרובעים

-


-

כל תלמיד יבחר נייר אוריגאמי ממניפת הצבעים.
לפעילות זו הכינו את המודד.
-

-

שאלה לדיון: איזה סוג מצולע הוא הנייר שקיבלתם? מה מיוחד במצולע זה?
-
יש לעודד את התלמידים לבסס את תשובותיהם
תוך הסתייעות במודד למדידה.
-

-

תשובה: צורת הנייר הוא מצולע הנקרא ריבוע. כל צלעותיו שוות באורכן.
-
יש להציג את התשובה בשקופית זו רק לאחר שהתלמידים בחנו את הנייר בצורת ריבוע.

-

-

הוראת קיפול: להצמיד קדקוד אל הקדקוד הנגדי ולפתוח.
-
מומלץ לא לתקן, לא לסדר או לגעת בעבודת התלמיד.

-

-

שאלה לדיון: מה השתנה בנייר בצורת ריבוע לאחר שקיפלנו למשולש ופתחנו בחזרה? הסבירו
-
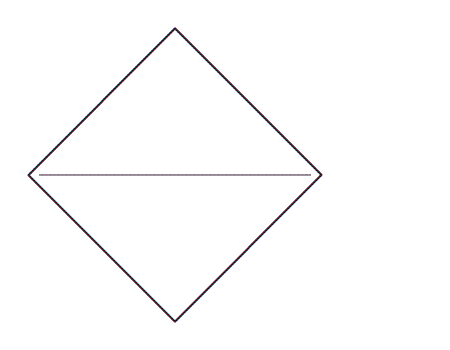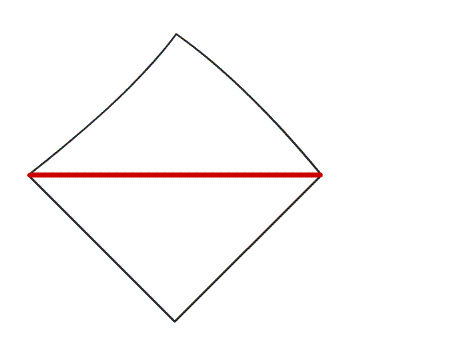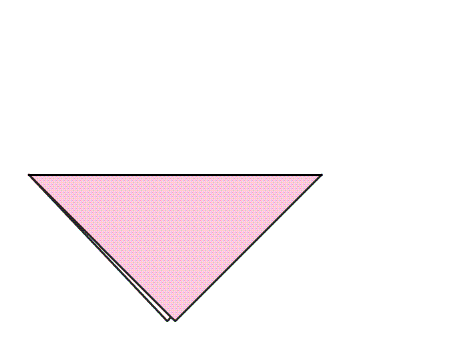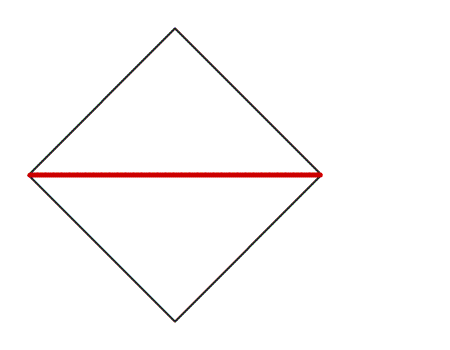

-

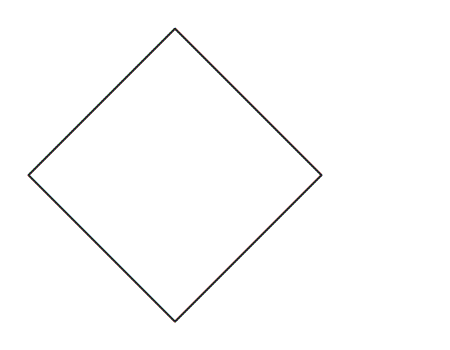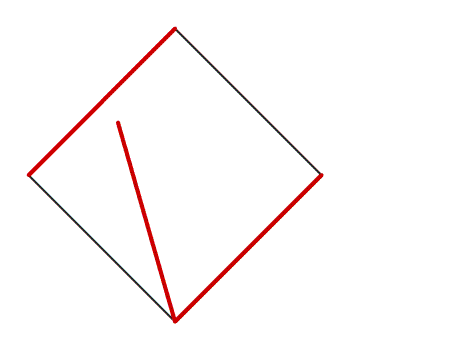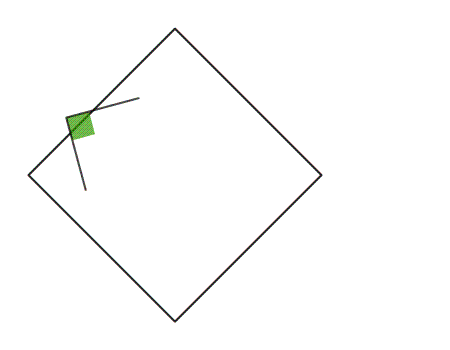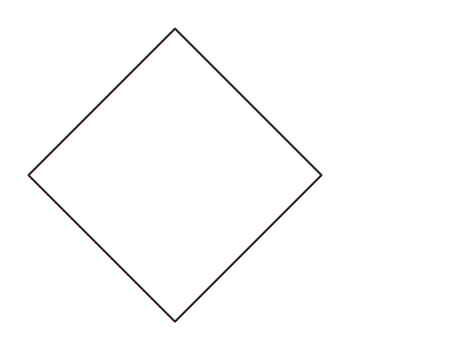
תשובה: לאחר שקיפלנו נייר בצורת ריבוע התקבל קו שיקוף המחלק את הריבוע ל- 2 משולשים חופפים.
-
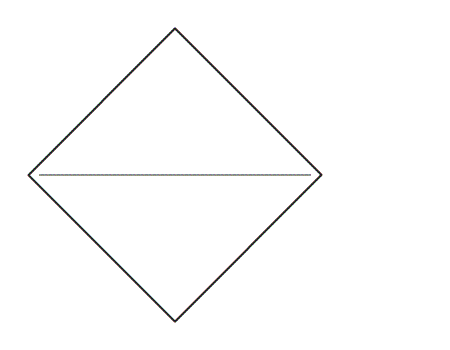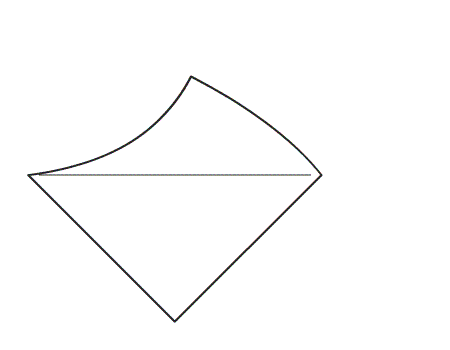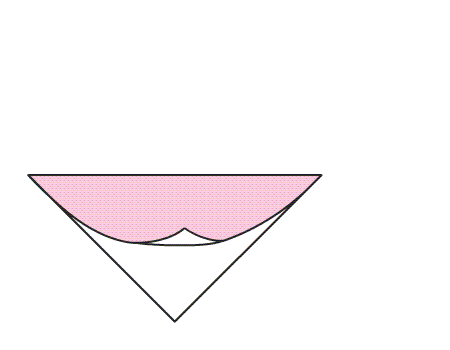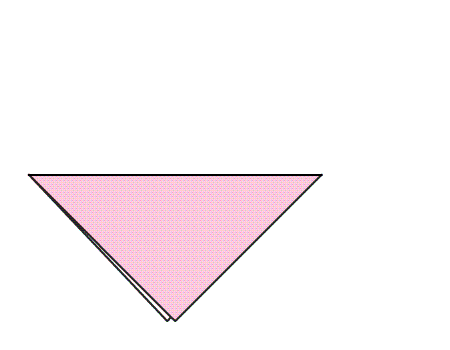

-

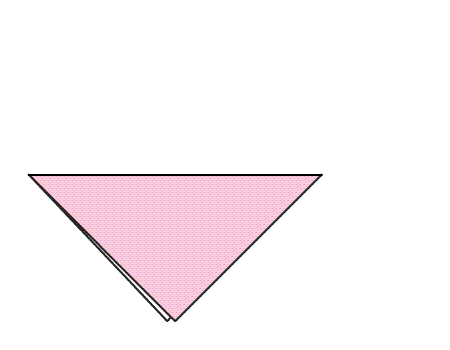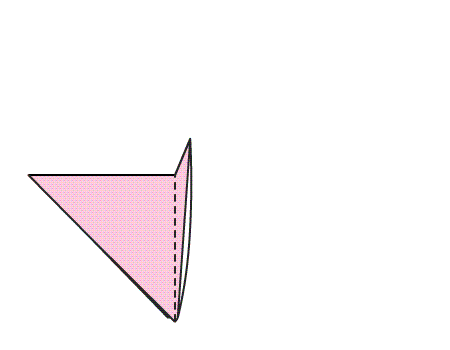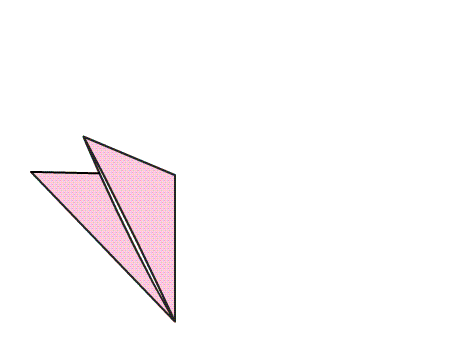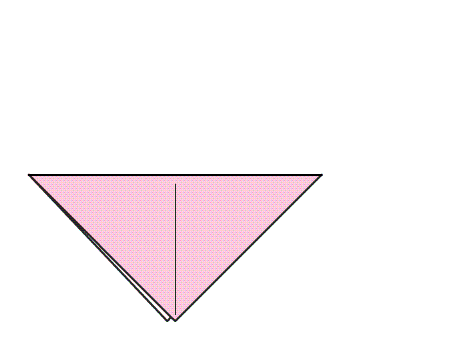
הוראת קיפול: להצמיד קדקוד אל הקדקוד הנגדי, כך שנקבל משולש.
-

-

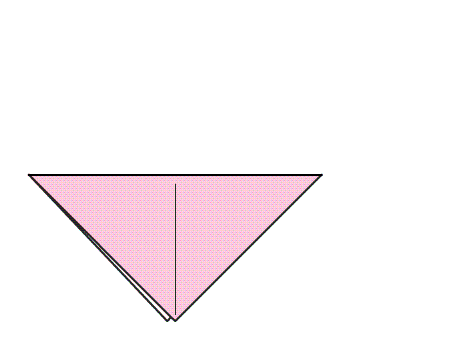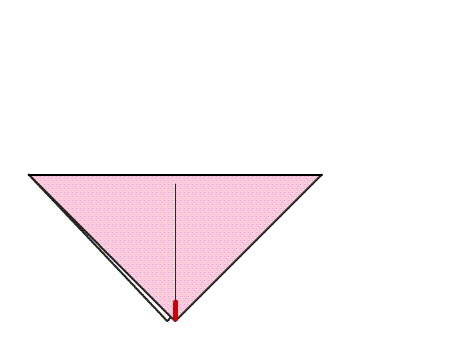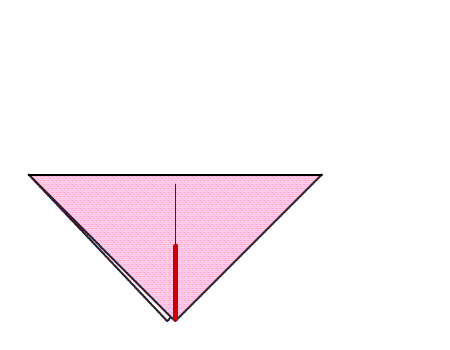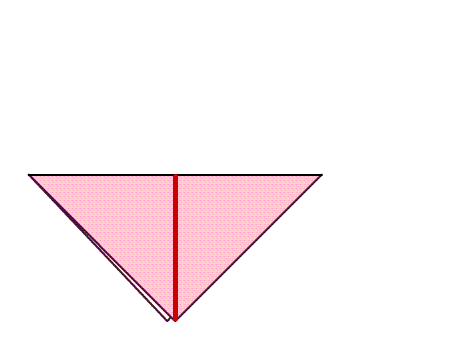
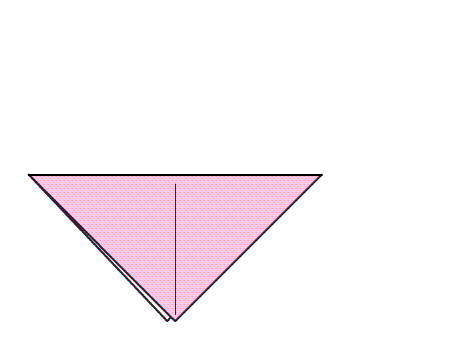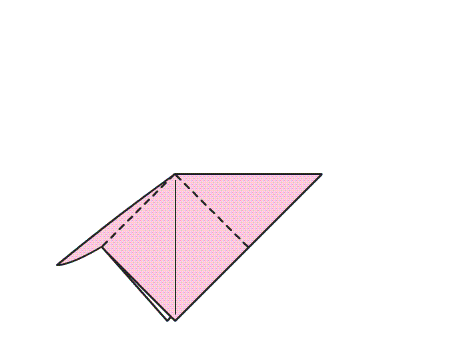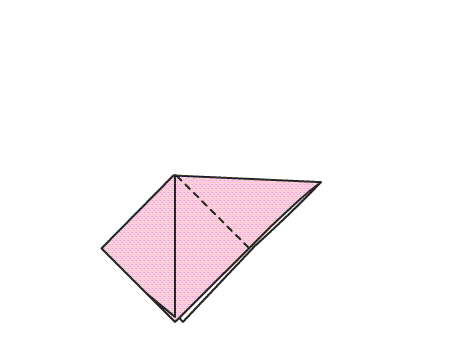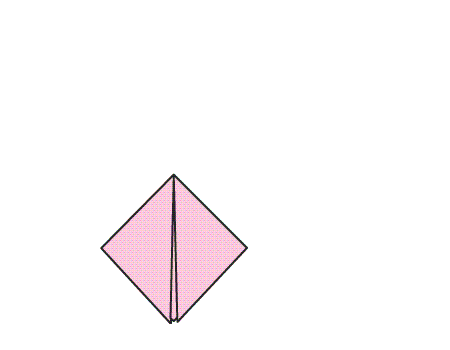
הוראת קיפול: במשולש שנוצר, לקפל קדקוד אל קדקוד ולפתוח בחזרה למשולש הגדול כפי שמסומן באנימציה.
-

-

שאלה לדיון: בחנו את הישר שנוצר במשולש בעקבות הקיפול, הסבירו.
-


-

תשובה: מצאנו שבקיפול, כפי שמודגם באנימציה, משולש אחד מכסה את המשולש השני בדיוק. לכן, הישר הוא קו השיקוף של המשולש.
-
מידע למורה: כאשר ישנו קו שיקוף, מומלץ לחזור שוב ושוב על המושג: “צורה אחת בקיפול מכסה בדיוק את הצורה השנייה”
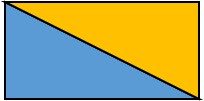
שימו לב: במלבן שתי הצורות חופפות (אם נגזור ונסובב הן יכסו אחת את השניה). שני המשולשים שמתקבלים בקיפול המלבן לאורך האלכסון, אינם מכסים זה את זה בדיוק בקיפול לאורך אלכסון זה.

-

-

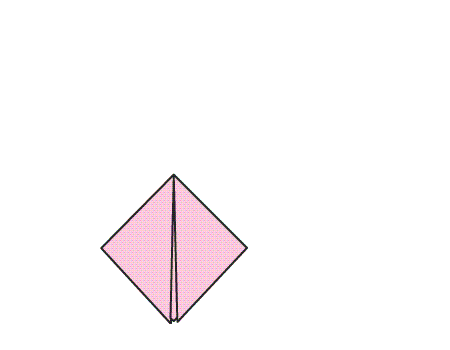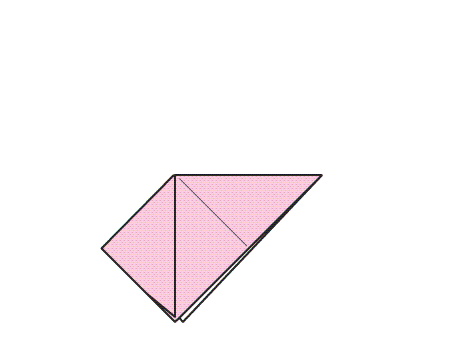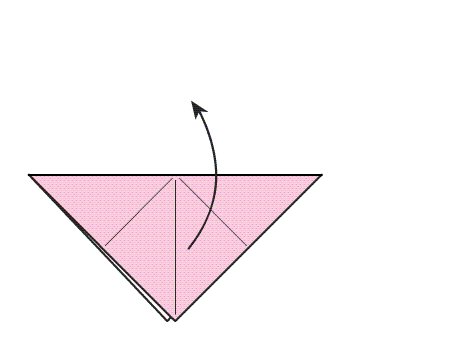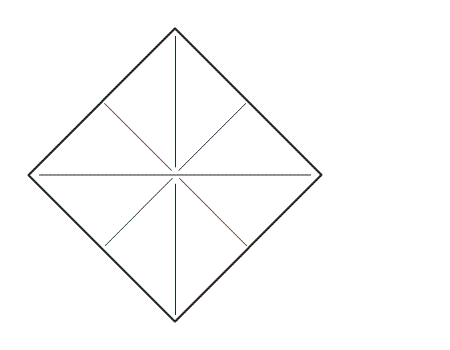
הוראת קיפול: בנייר המקופל למשולש, לקפל קדקוד לקדקוד.
-

-

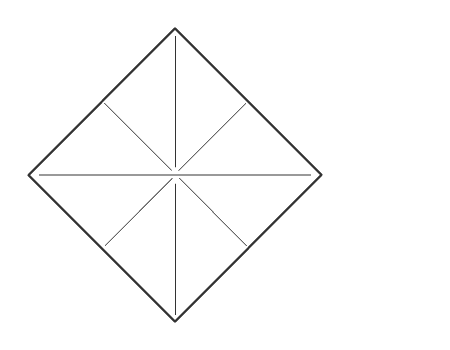
הוראת קיפול: לפתוח את הקיפולים שבנייר המקופל בחזרה לריבוע.
-

-

שאלה לדיון: בחנו את הריבוע: אילו מהישרים הם קווי השיקוף של הריבוע? כיצד נבחן זאת.
-
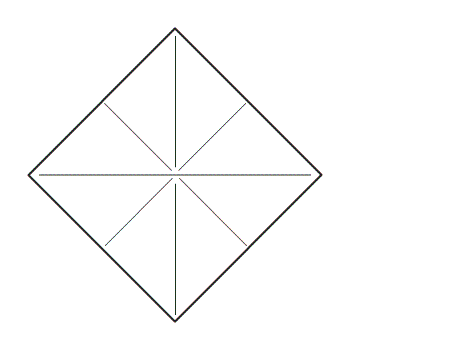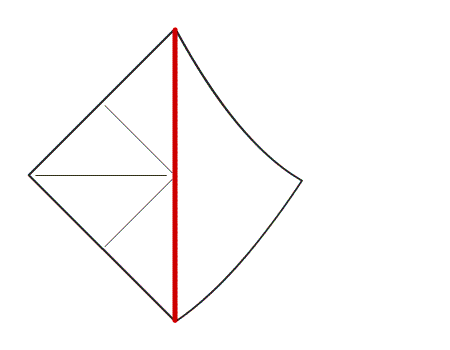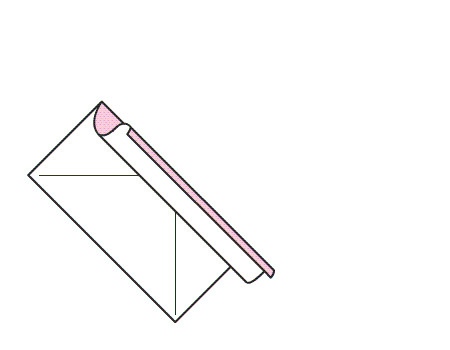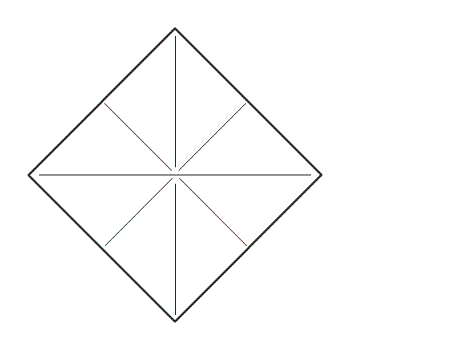

-

תשובה: כל הישרים הם קווי השיקוף של הריבוע מכיוון שבקיפול הריבוע בקווי השיקוף צורה אחת מכסה את השניה.
-
מומלץ לבקש מהתלמידים לשרטט את הישרים על הנייר תוך שימוש במודד כסרגל.

-


-

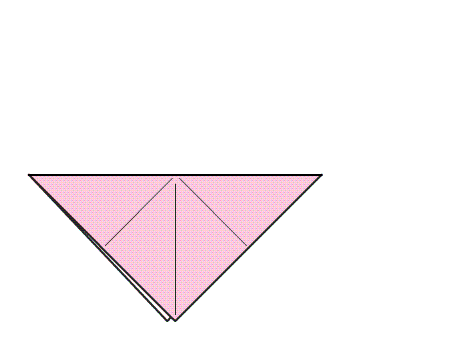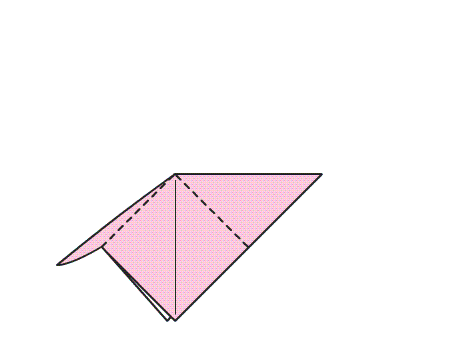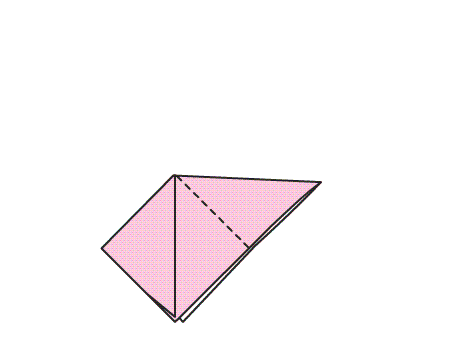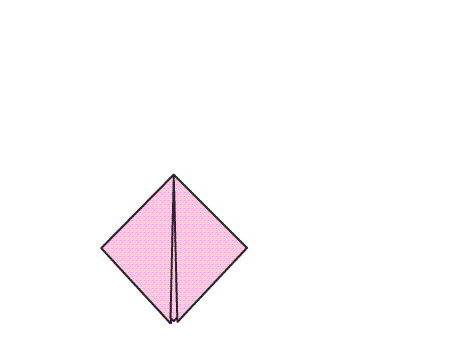
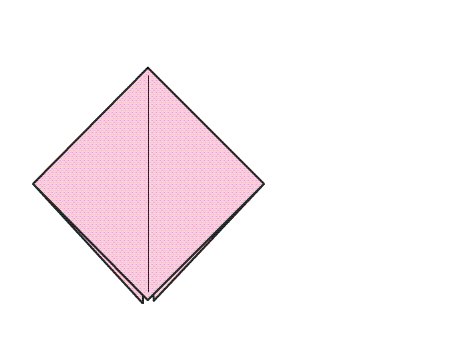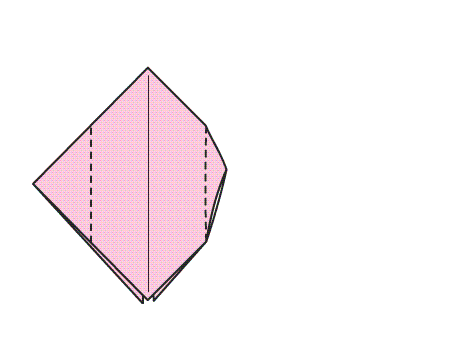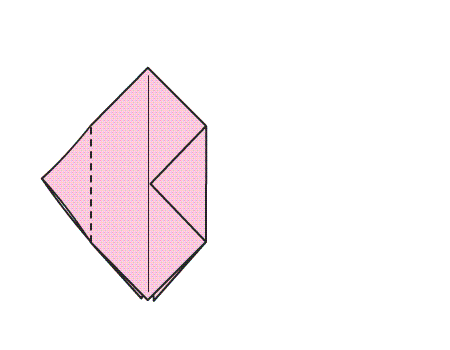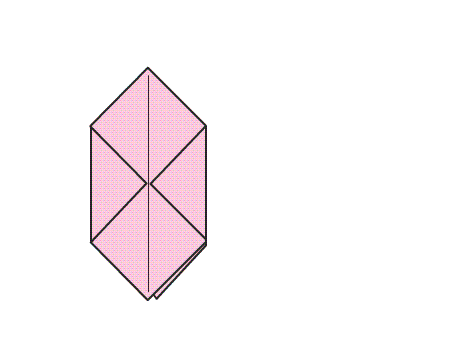
הוראת קיפול: להצמיד קדקוד אל הקדקוד הנגדי.
-

-

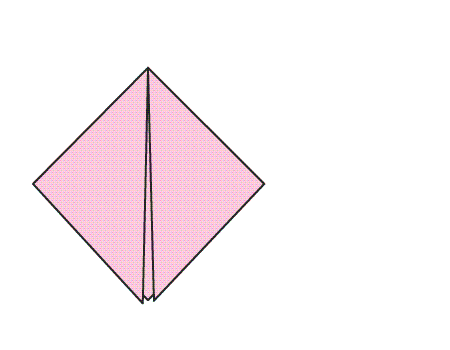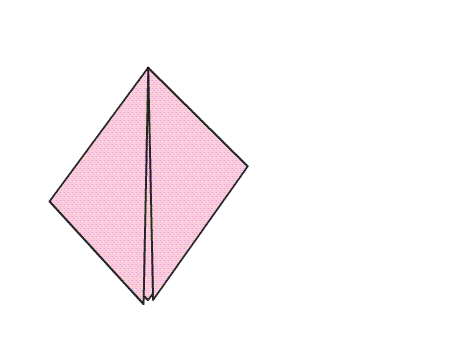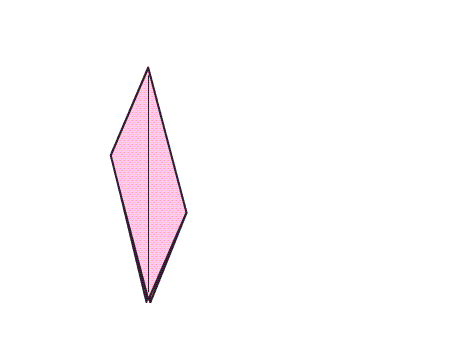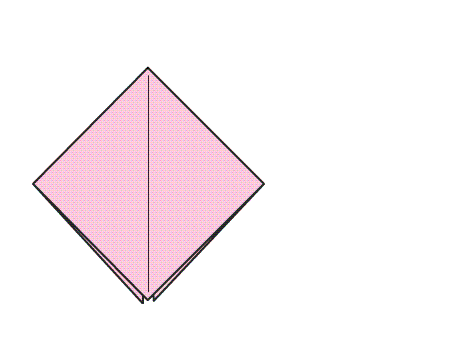
הוראת קיפול: לקפל את שני הקדקודים של המשולש המקופל אל הקדקוד בעל הזווית הישרה.
-

-

הוראת קיפול: הפכו את הריבוע שהתקבל לצד השני.
-
יש לעבור בין התלמידים ולוודא שהפכו את הנייר לצד השני.

-

-

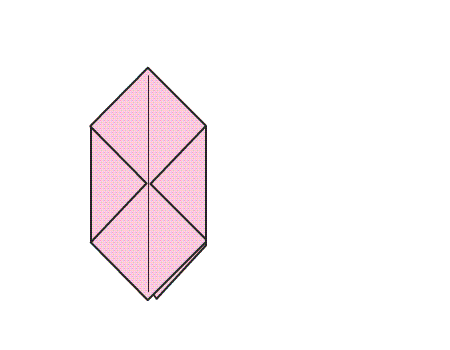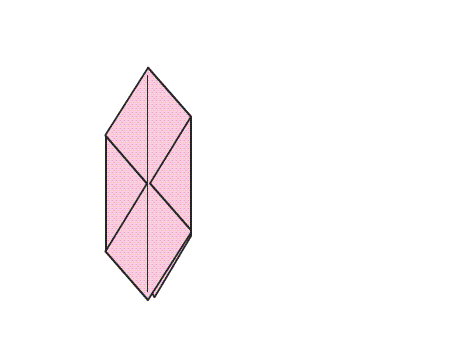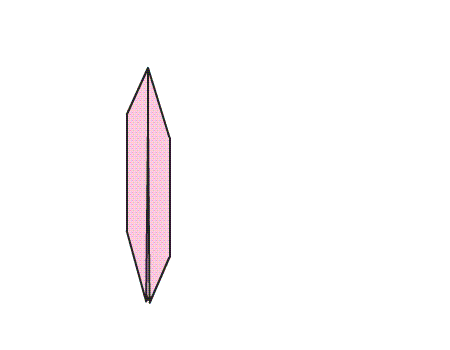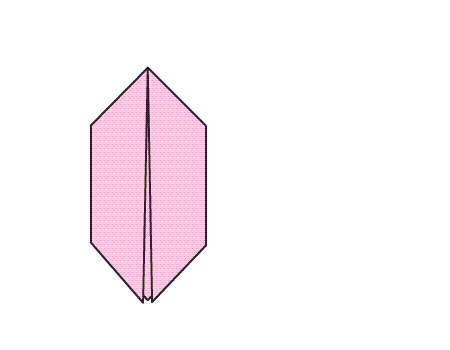
הוראת קיפול: לקפל בנייר המקופל, את כל אחד משני הקדקודים אל קו השיקוף כפי שמודגם באנימציה.
-

-

הוראת קיפול: להפוך את הנייר המקופל לצד השני.
-

-

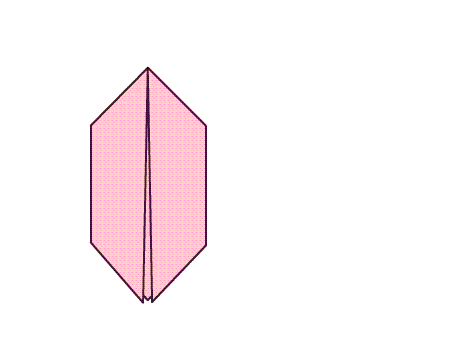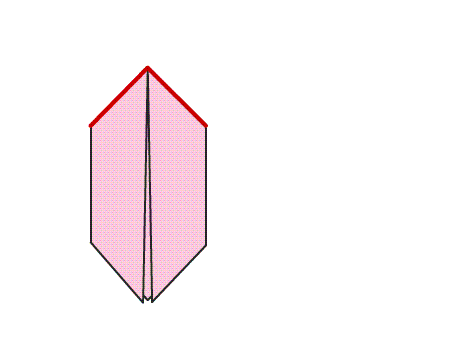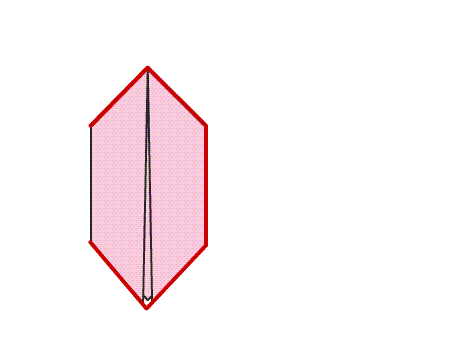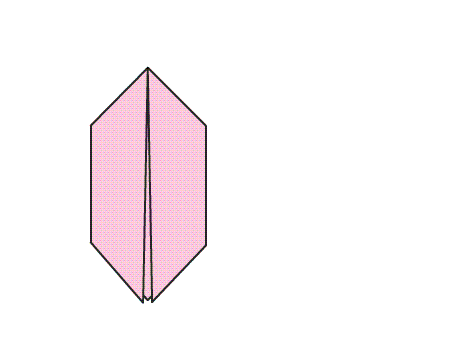
שאלה לדיון: בחנו את הנייר המקופל, איזה סוג מצולע קיבלנו? נמקו.
-

-

תשובה: קיבלנו מצולע בעל 6 צלעות ו- 6 קדקודים, הנקרא משושה.
-


-

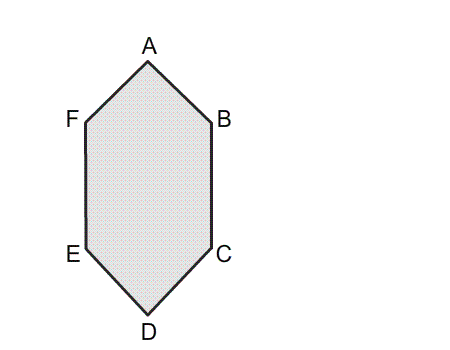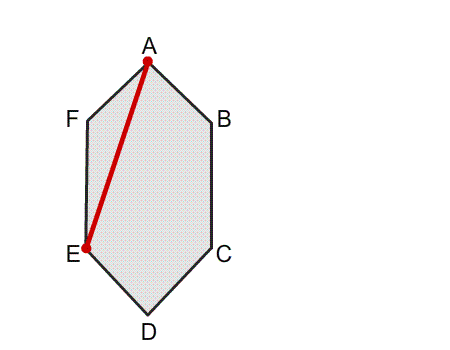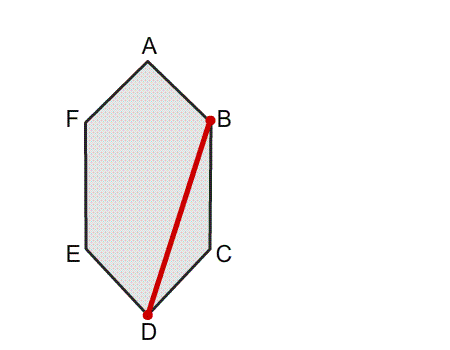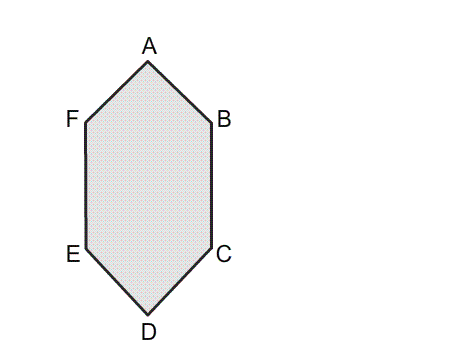
שאלה לדיון: האם ניתן לזהות קווי סימטריה בנייר המקופל בצורת משושה? נמקו.
-

-

תשובה: למשושה שני קווי שיקוף. כאשר נקפל את שני חלקי המשושה הם יכסו זה את זה בדיוק.
-

-

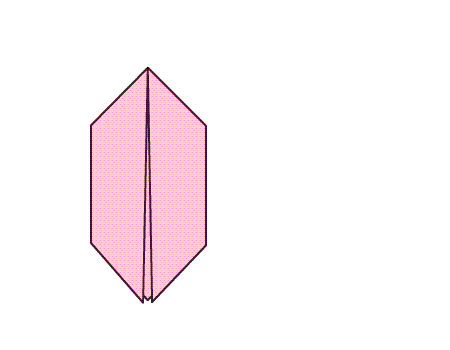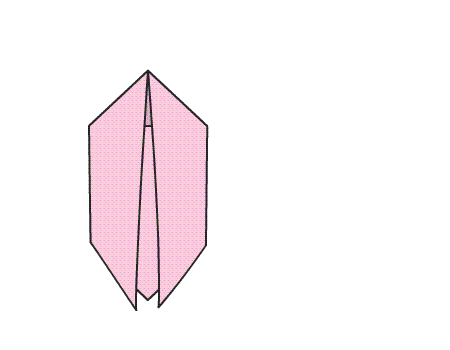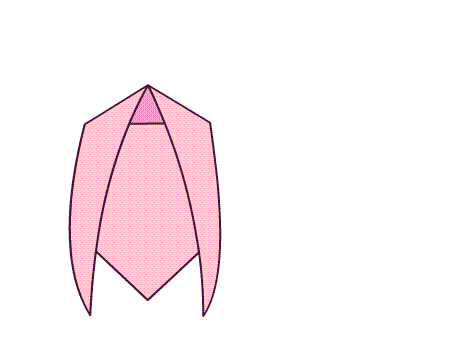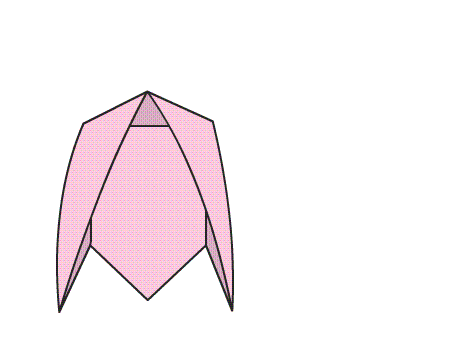
הוראת קיפול: הניחו את הנייר בצורת משושה על השולחן, ופיתחו את הטרפזים.
-
יש להדגיש בפני התלמידים כי עליהם לקפל על השולחן.

-
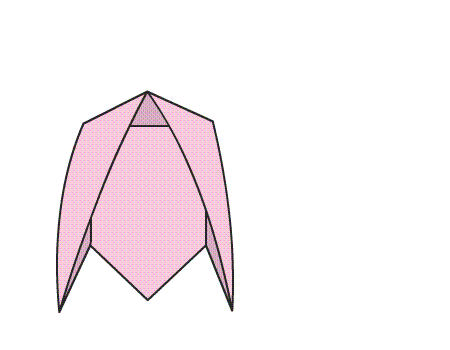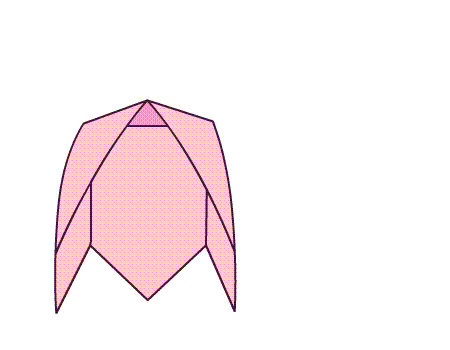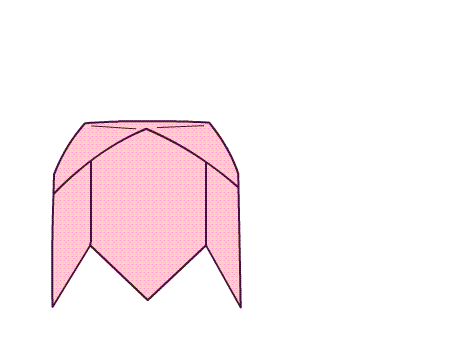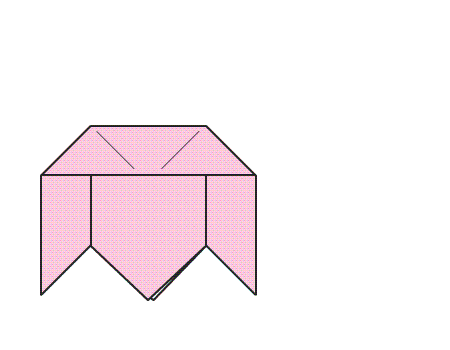

-

הוראת קיפול: לשטח את הטרפזים המקופלים לפי הסימון באנימציה.
-
יש להדגיש בפני התלמידים כי גם על הוראת קיפול זו להתבצע כאשר הדגם על השולחן.

-


-

הוראת קיפול: להפוך את הנייר המקופל לצד השני.
-


-

הוראת קיפול: לקפל את קדקודי הזווית הישרה למשולש קטן.
-


-

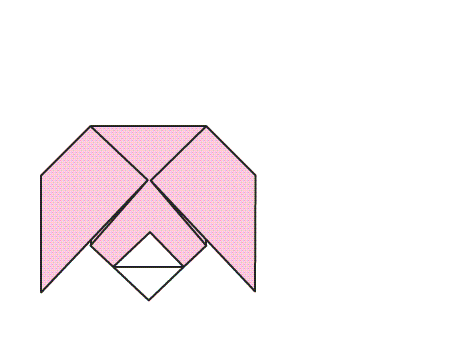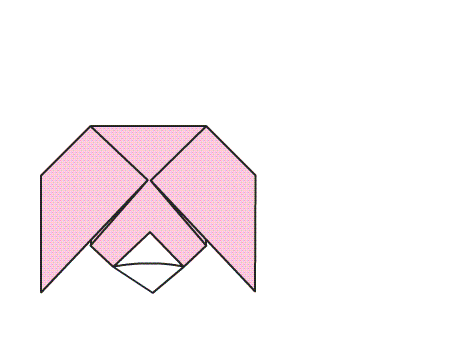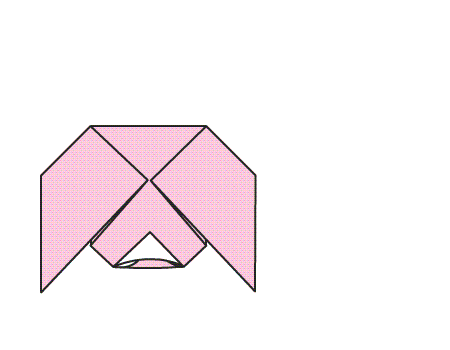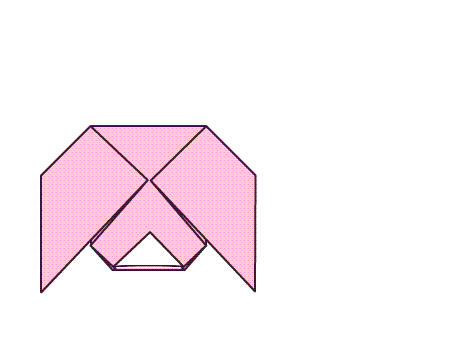
הוראת קיפול: לפתוח את אחד מהמשולשים הקטנים.
-

-

הוראת קיפול: להכניס פנימה את המשולש הקטן לפי האנימציה.
-
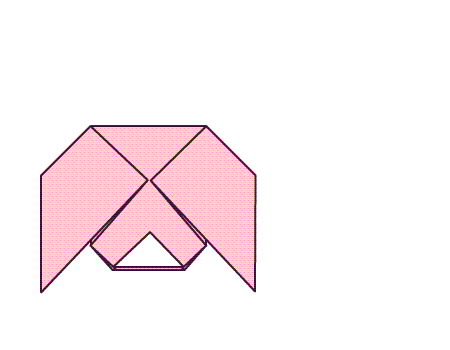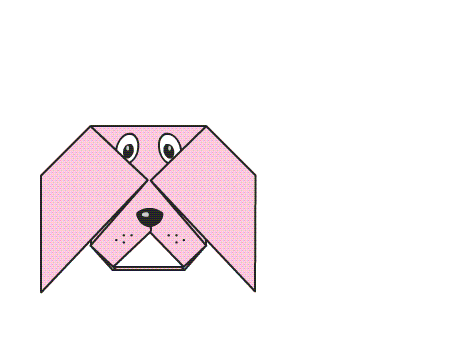

-

הוראת קיפול: ציירו לכלבלב המקופל פנים.
-


-

הוראת קיפול: הפכו את הנייר המקופל לצד השני וציירו פנים גם לילדה.
-


-

אתם מוזמנים לעצב ולצייר. מומלץ לעצב ולצייר כפי שאתם אוהבים.
-
מומלץ לעודד את התלמידים לעצב וליצור את התוצר הסופי כפי שהדמות נראית להם.

- מטרות הפעילות
- התלמידים יצרו צורות בשיקוף על-ידי פעילות בקיפולי נייר.
- התלמידים יזהו אם שתי צורות מתקבלות זו מזו בשיקוף.
- התלמידים יגלו את תכונות השיקוף במהלך קיפול הדגם.
- התלמידים ימצאו את מקומו של קו השיקוף.
- שם הדגם
ילדה \ כלבלב.
מספר סידורי: 1011
- יוצר/ת הדגם
מירי גולן
© כל הזכויות שמורות למרכז הישראלי לאוריגאמי
- רצף מומלץ
מומלץ ללמד לפי הרצף המופיע באתר (הרצף על פי תכנית הלימודים).
- על השיעור
בשיעור זה יחקרו התלמידים את קווי השיקוף במרובעים המתהווים במהלך הקיפול, ויבחנו אם הם קווי השיקוף. בסיום השיעור מתקבל התוצר הסופי כהפתעה, תוך לימוד מושגים חדשים וחזרה על המושגים שנלמדו בשיעורי ההכנה. בפעילות זו נבחן את קווי השיקוף על-ידי קיפול, ונבדוק אם צד אחד מכסה את הצד השני.
משך זמן פעילות מומלץ: 90 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ידע נדרש
הכרת המצולעים.
- ציוני דרך לפי כיתות
- חומרים
- נייר אוריגאמי לכל תלמיד בגודל 15/15 ס”מ, שני טושים בצבעים שונים ומודד


מיכל צוברי
דצמבר 6, 2016שלום וברכה,
בשקופית 23 האנימציה הראתה שיש קו שיקוף אחד, אך למעשה יש 2 קווי שיקןף, השני הוא באמצע המשושה לרוחב, לא מקדקד לקדקד.
תודה.
Miri Golan
ינואר 6, 2017הי מיכל
תודה על המשוב את צודקת אכן ישנם שני קווי סימטריה
נעשה תיקון בשיעור
מירי