חקר מרובעים 1 (ריבוע, מעוין, ומקבילית)

כל תלמיד מקבל 3 ניירות אוריגאמי ממניפת הצבעים.

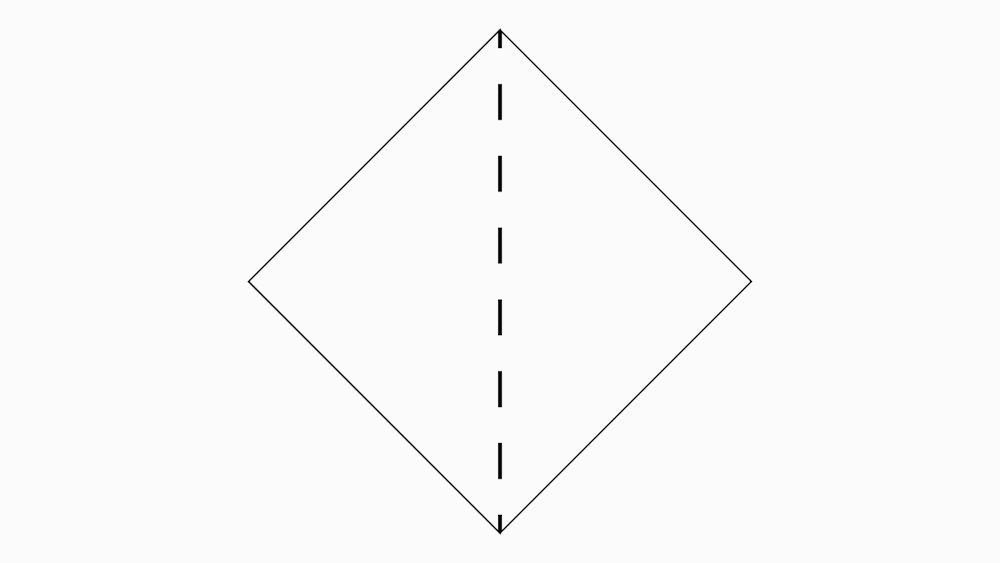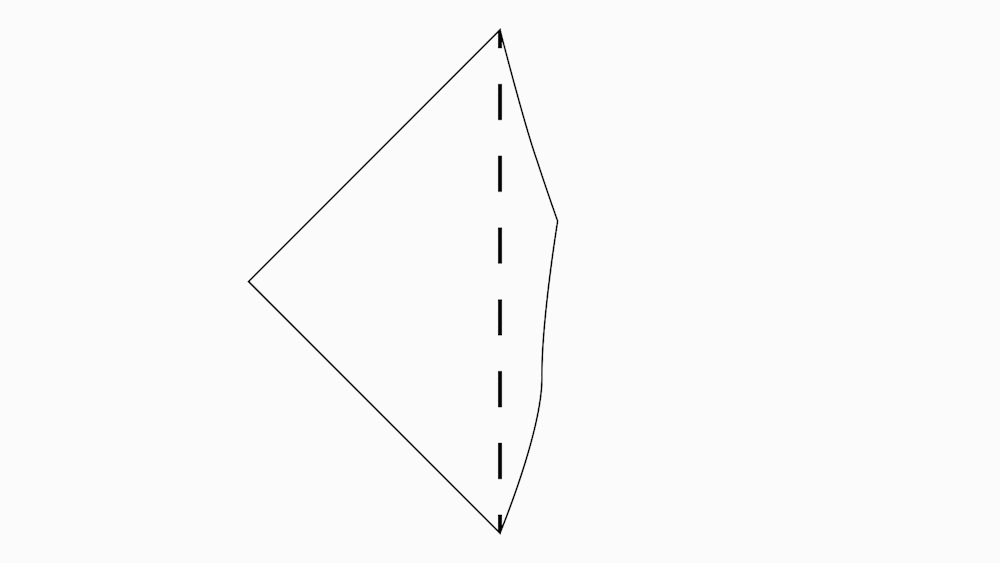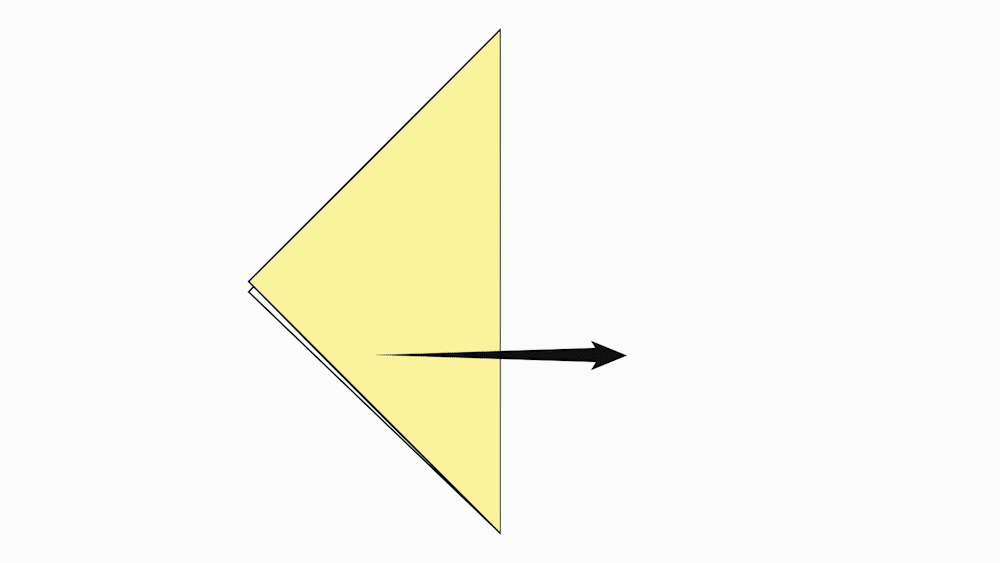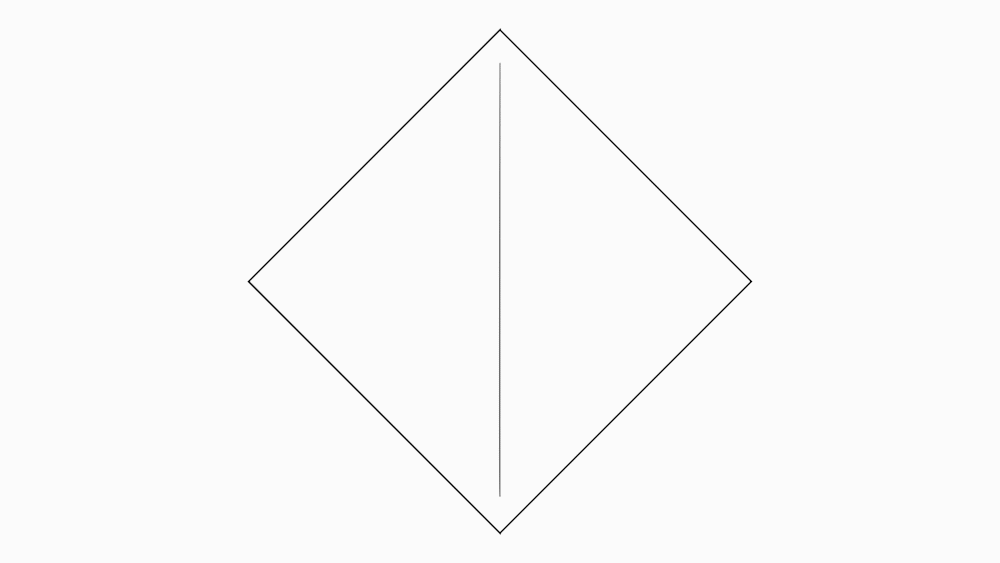
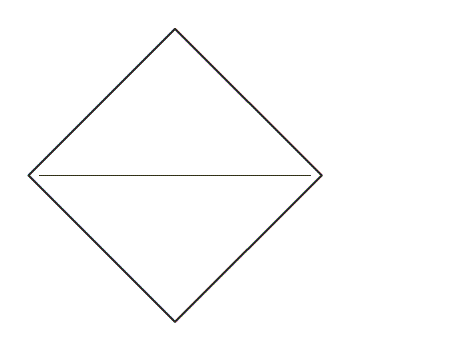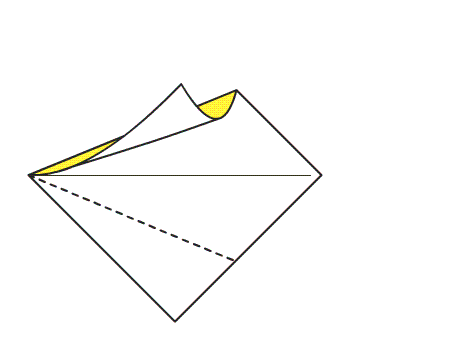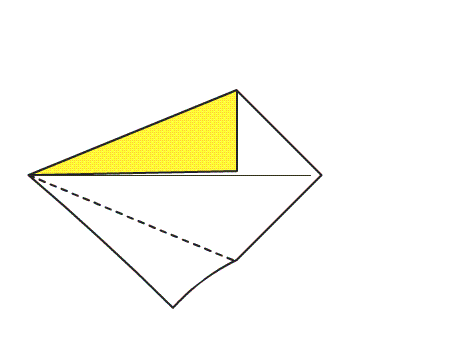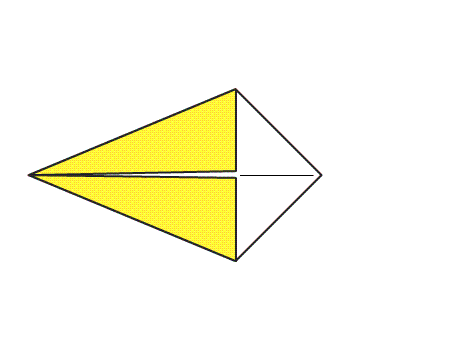
הוראת קיפול: לקפל קדקוד לקדקוד נגדי ולפתוח בחזרה לריבוע.(ב-3 ניירות)

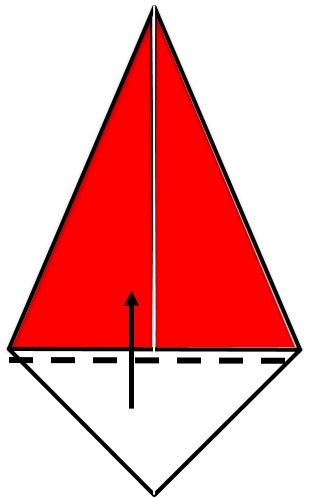
הוראת קיפול: לקפל שתי צלעות של הריבוע אל האלכסון. (ב-3 ניירות)

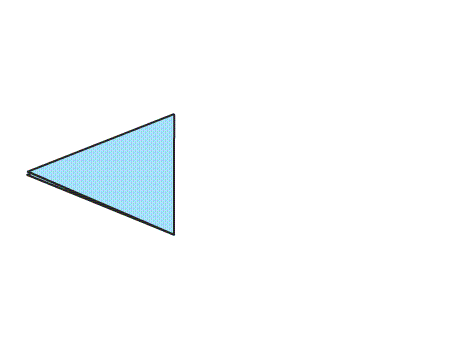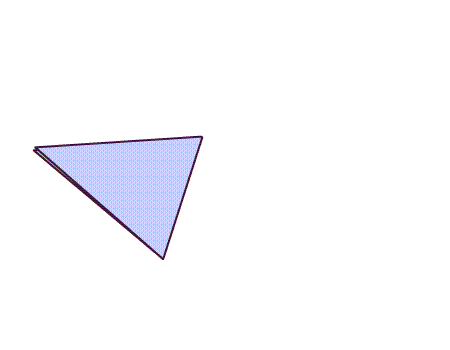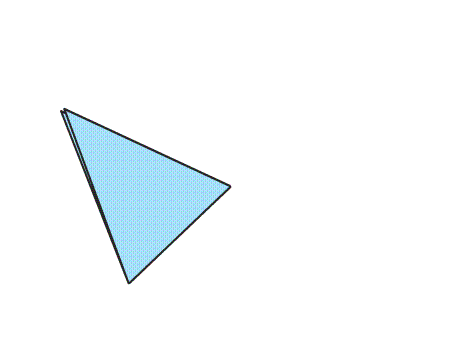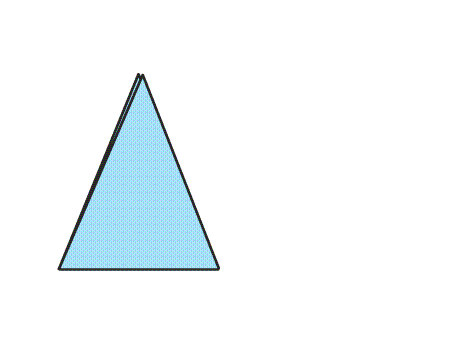
הוראת קיפול: לקפל את המשולש הלבן מעל שני המשולשים הצבעונים. (ב-3 ניירות)

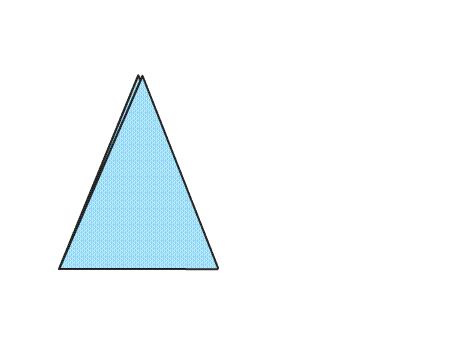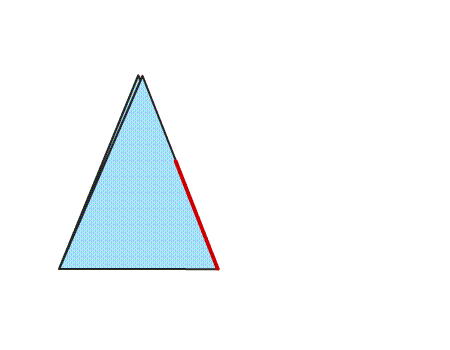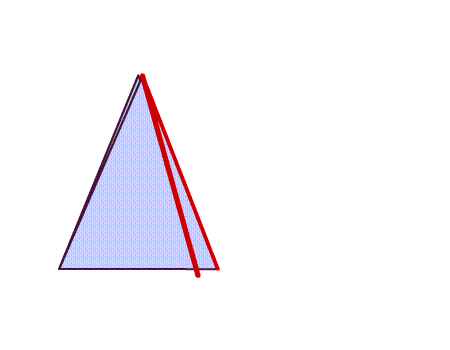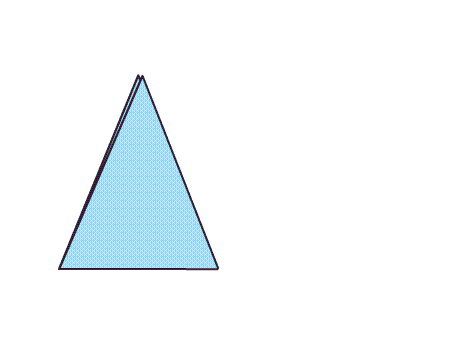
שאלה לדיון: איזה סוג משולש התקבל? נמקו

תשובה: המשולש הוא שווה שוקיים וחד זוויות.

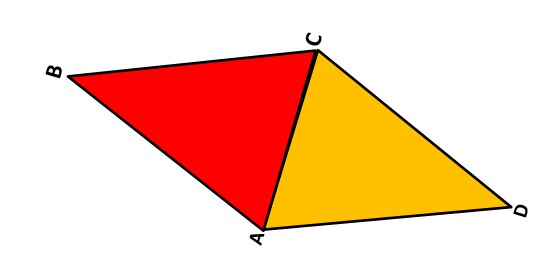
משימה: הצמידו את שני המשולשים כך שיתקבל מרובע : שכל הצלעות שלו שוות באורכן. כל זוג צלעות מקבילות שוות זו לזו. וכל זוג זוויות נגדיות שוות זו לזו.

שאלה לדיון: האם במצולע שמצאתם האלכסונים מאונכים וחוצים זה את זה, והאם האלכסונים חוצים את הזוויות.

שאלה לדיון: האם זה המרובע שהתקבל?

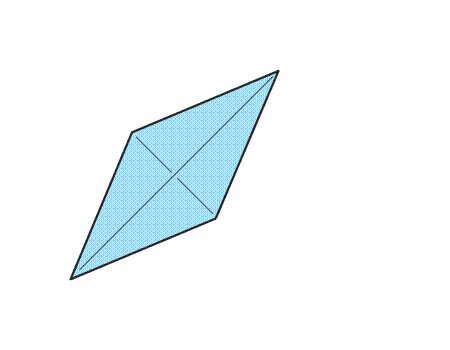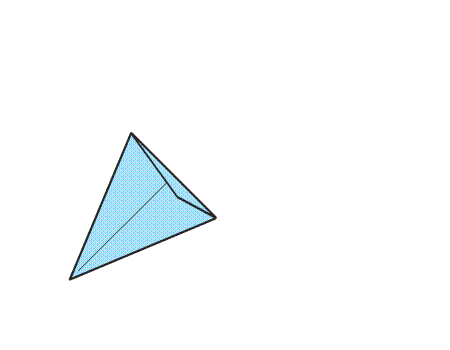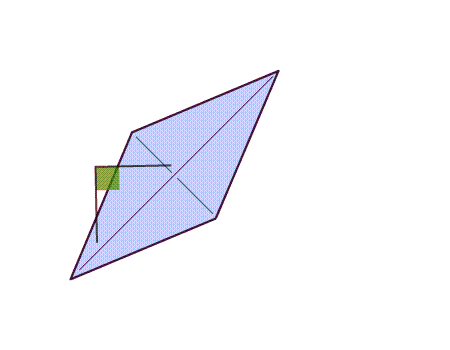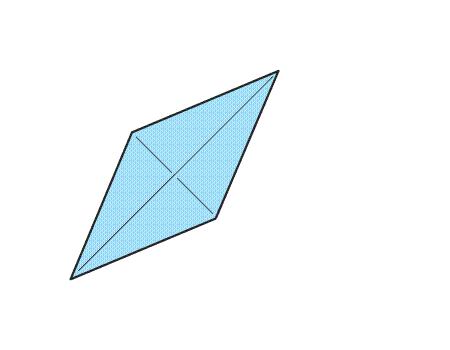
שאלה לדיון: מה ניתן לומר על המצולע שהתקבל?

תשובה: למצולע שהתקבל 4 צלעות שוות באורכן וכל שתי זוויות נגדיות שוות זו לזו ולכן המצולע הוא מעוין.

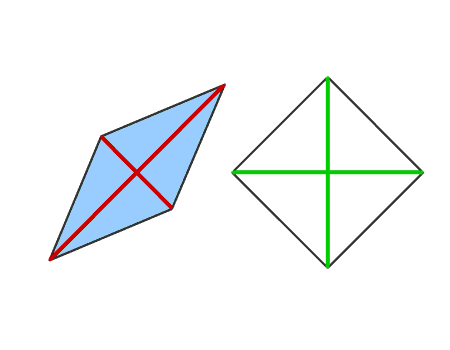
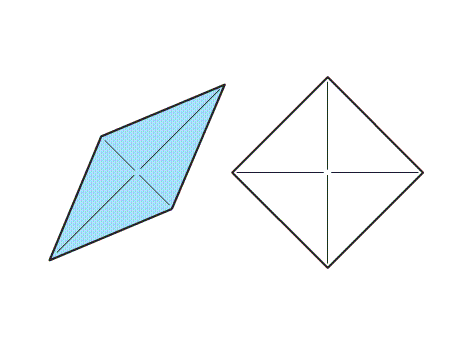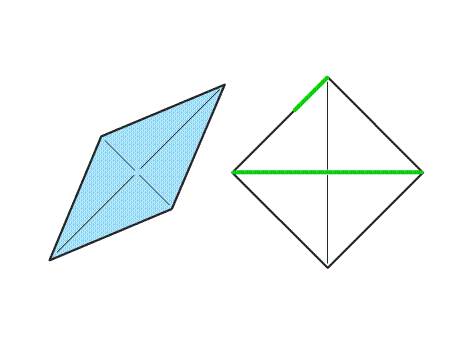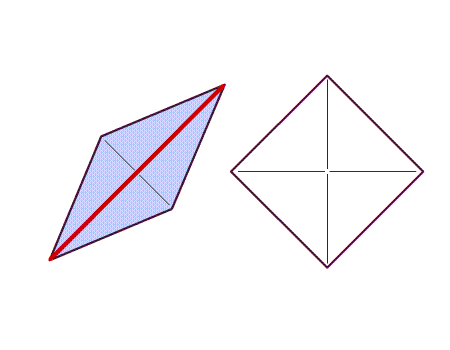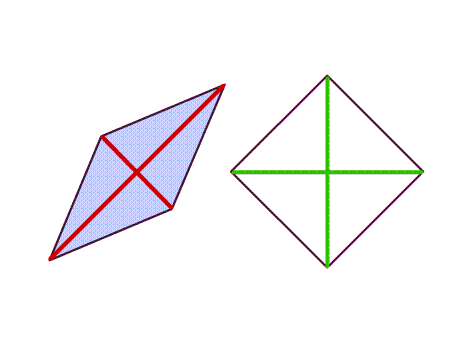
שאלה לדיון: במה האלכסונים של הריבוע והמעוין דומים, ובמה הם שונים? נמקו

האלכסונים של הריבוע והמעוין דומים בכך, שהם חוצים זה את זה ומאונכים זה לזה. האלכסונים הם גם קווי הסימטריה של הריבוע והמעוין.

האלכסונים של הריבוע והמעוין שונים:  בריבוע האלכסונים שווים זה לזה באורכם. ובמעוין האלכסונים אינם שווים זה לזה.

משימה: הצמידו את שני המשולשים כך שיתקבל מרובע : שבו כל זוג צלעות נגדיות מקבילות ושוות זו לזו. שכל זוג זוויות נגדיות שוות זו לזו.  ושהאלכסונים יחצו זה את זה.

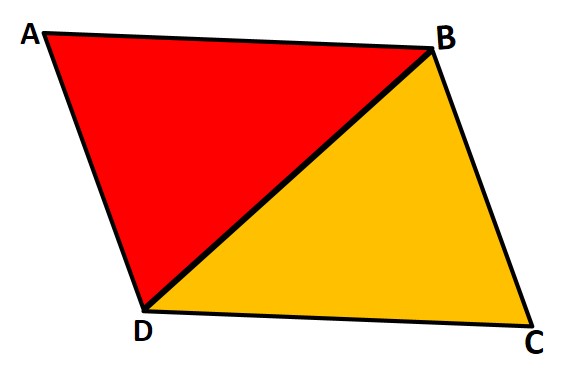
שאלה לדיון: האם זה המרובע שהתקבל?

שאלה לדיון: בחנו את האלכסונים של המקבילית? מה גיליתם? נמקו

תשובה: למקבילית אלכסון אחד בין הקדקודים D ל-B. ואלכסון נוסף,  בין הקדקודים  A ל-C. הוא אינו מסומן באיור זה, אך תוכלו לסמן את שני האלכסונים של המקבילית בדף העבודה.

משימה: הצמידו את המשולשים כך שיתקבל מרובע שלו זוג אחד של צלעות מקבילות.

שאלה לדיון: האם זה המרובע שהתקבל? באיזה אופן בחנתם את הצלעות המקבילות?הסבירו

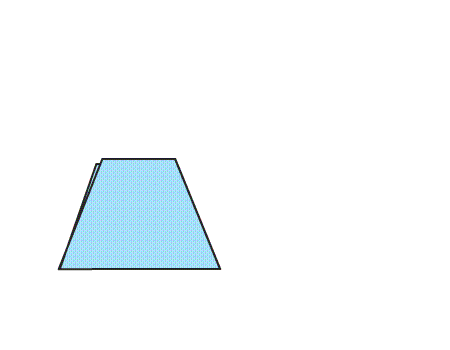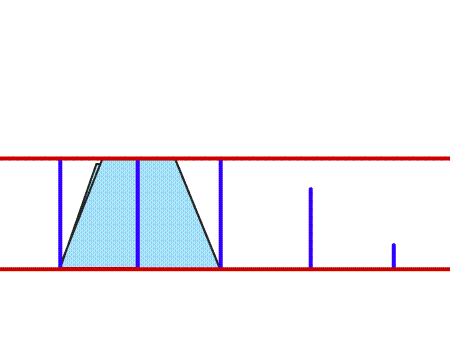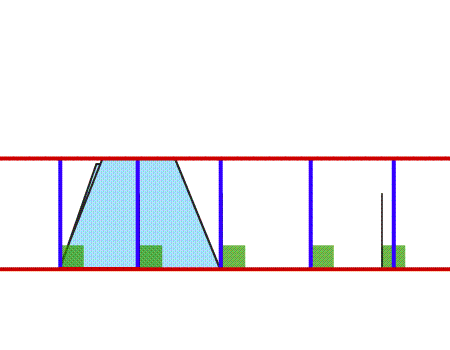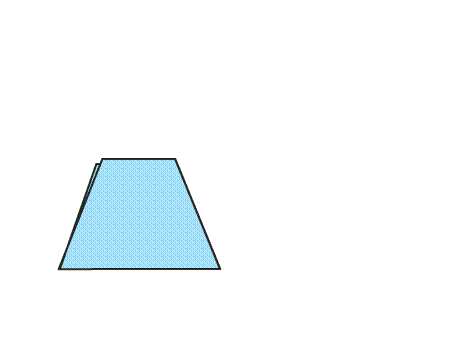
תשובה: המרובע שהתקבל הוא טרפז, לטרפז זוג אחד של צלעות מקבילות. בחנו את הצלעות המקביליות על ידי הישרים המאונכים.

משימת סיכום: האם תוכלו ליצור מרובעים נוספים?