Sorry, you have Javascript Disabled! To see this page as it is meant to appear, please enable your Javascript! See instructions here

חלק מהשלם 1/5- חלק ג

חלק מהשלם 1/5- חלק ג

חלק מהשלם 1/5- חלק ג

- כל תלמיד יבחר נייר אחד בגודל 15ס”מ/ 15ס”מ
  ושני ניירות קטנים 9 ס”מ/ 9ס”מ.
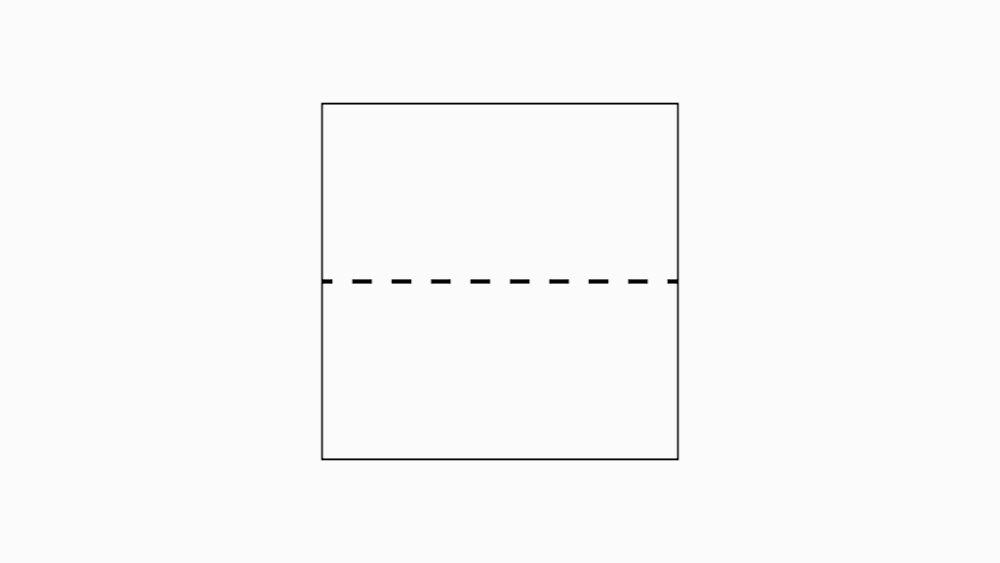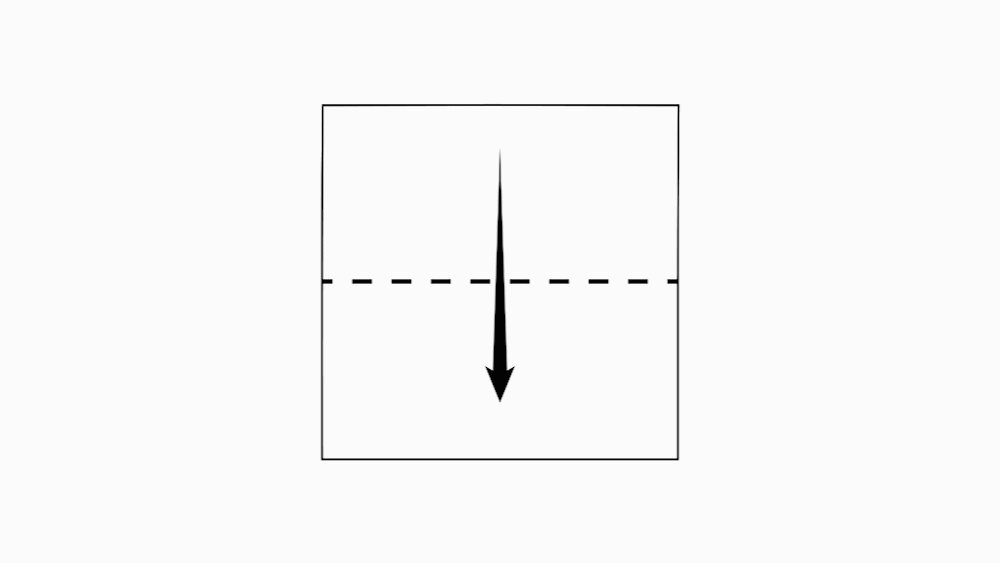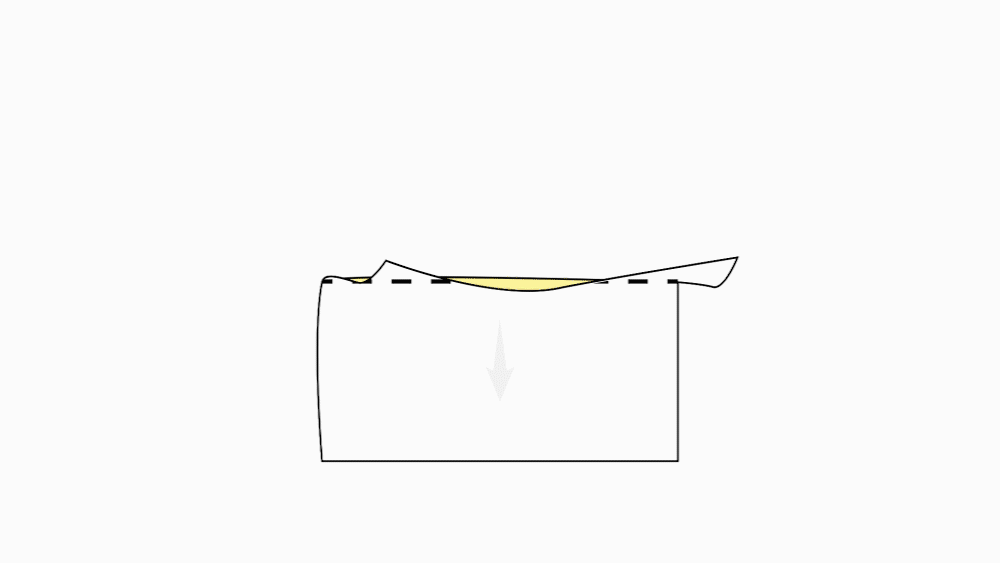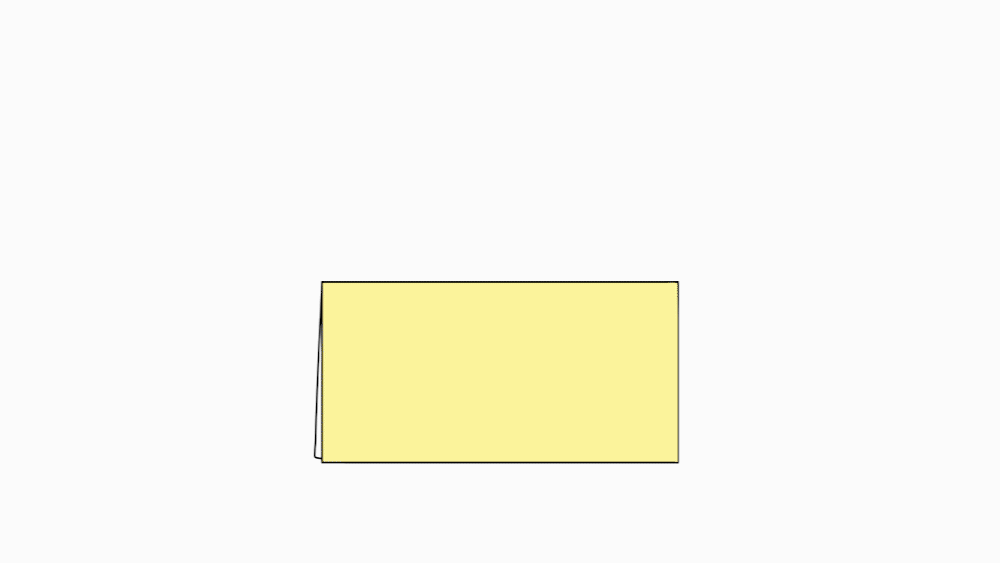
- הוראת קיפול: לקפל צלע לצלע מקבילה ולפתוח (לקפל בנייר הגדול בלבד).
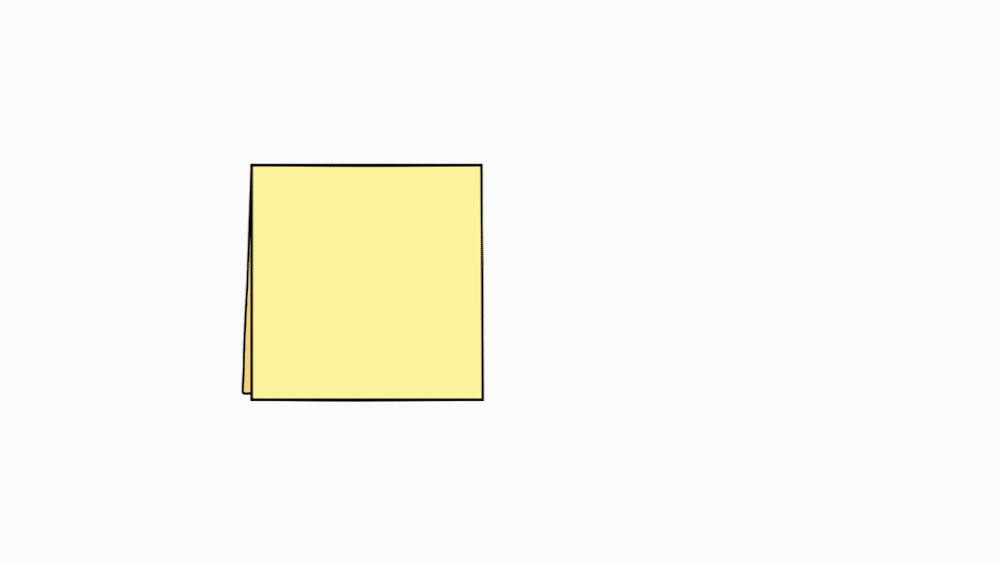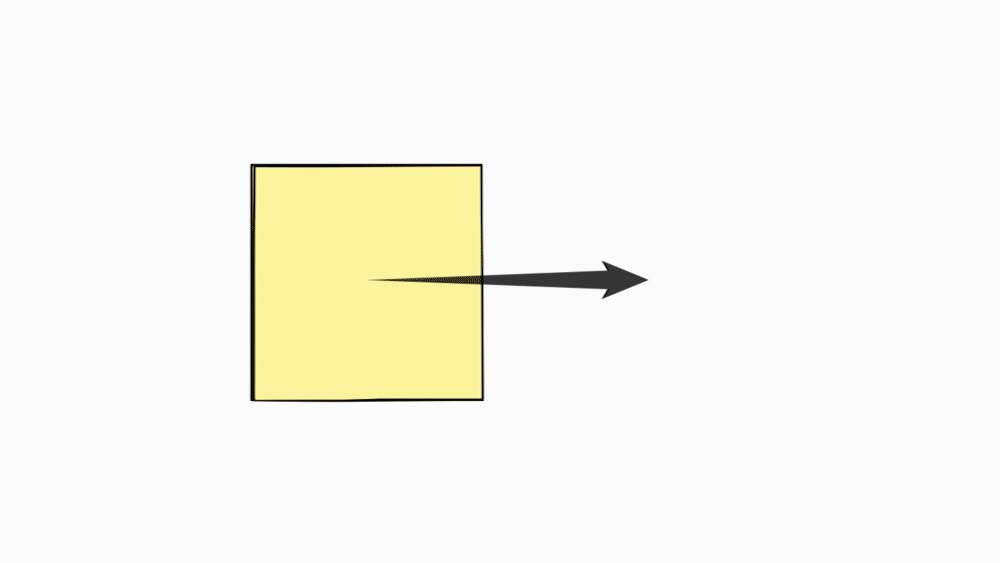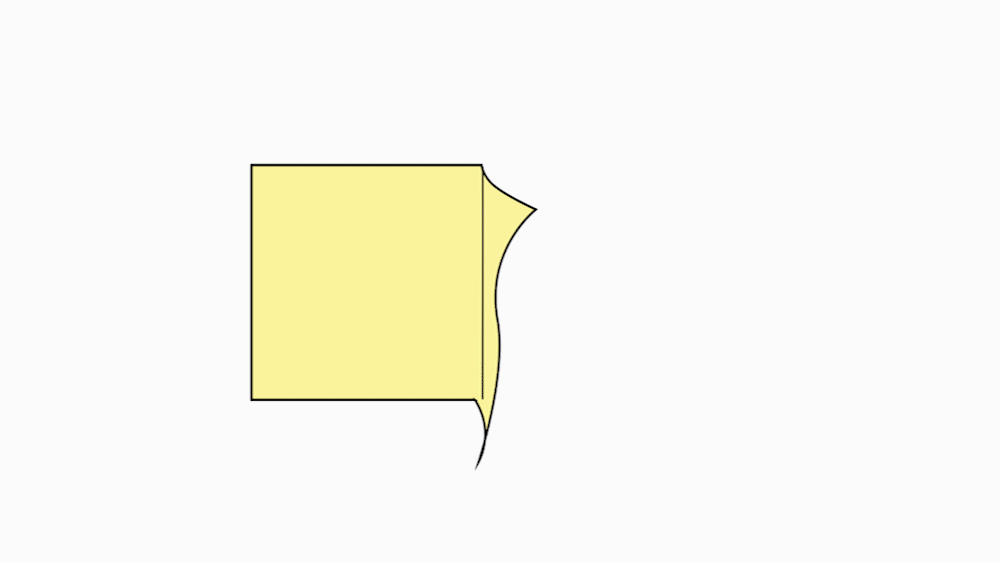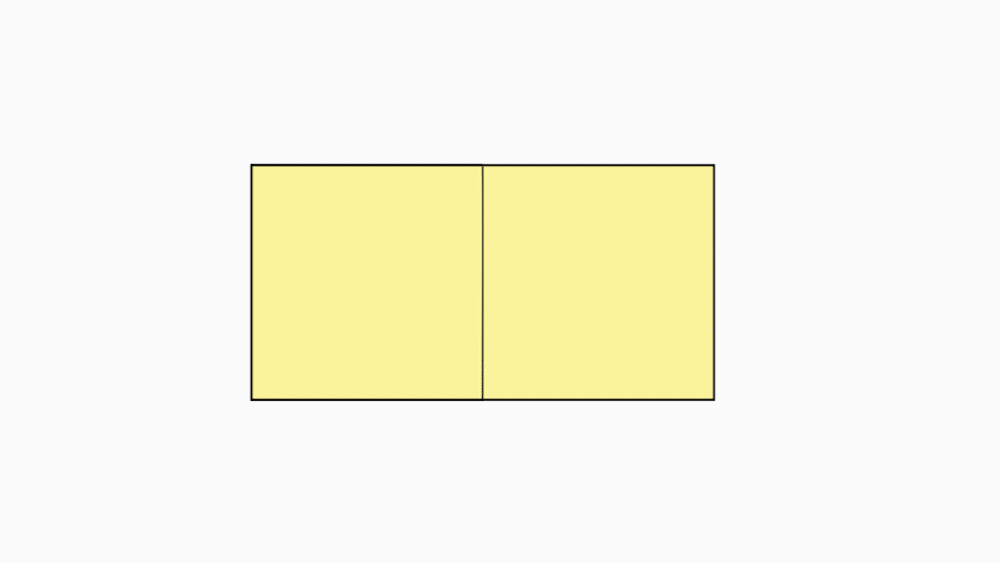
- הוראת קיפול: לקפל קצרה לצלע מקבילה ( לקפל בנייר הגדול בלבד).
- הוראת קיפול: לפתוח בחזרה למלבן (לקפל בנייר הגדול בלבד).
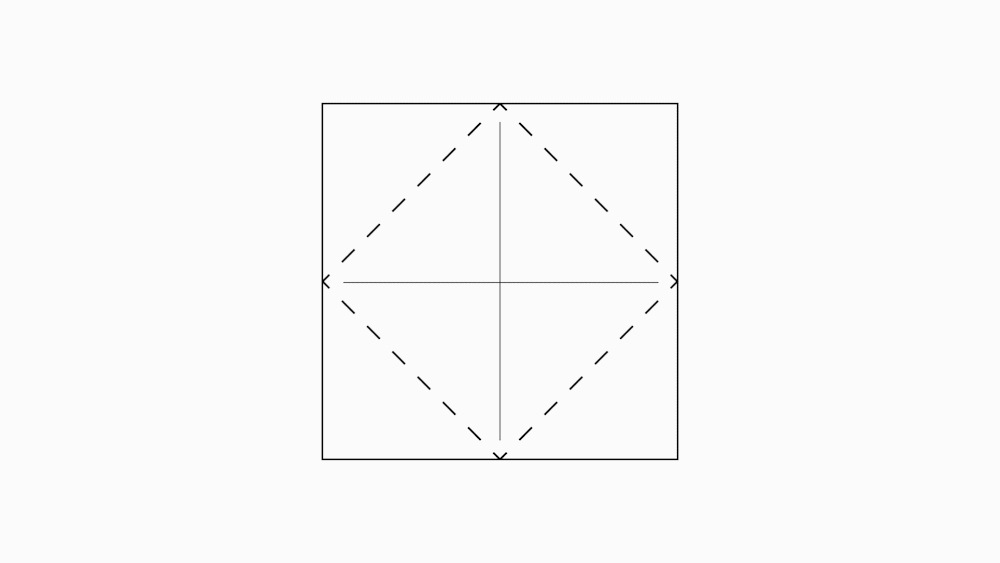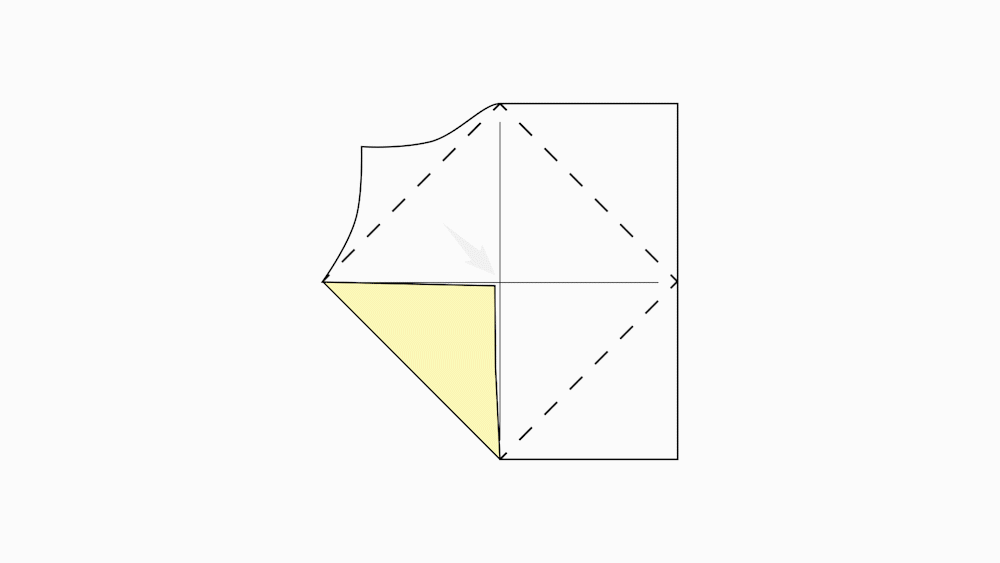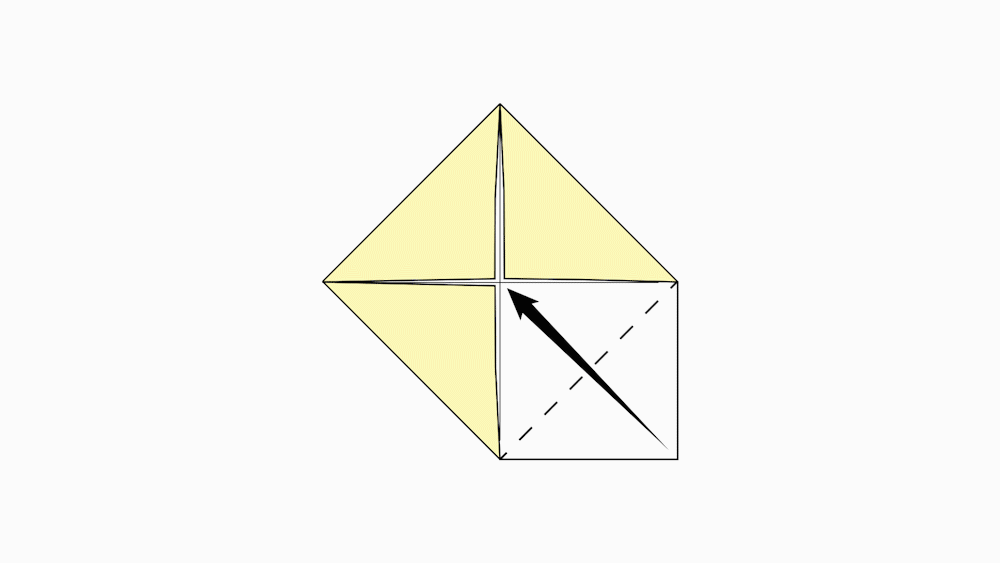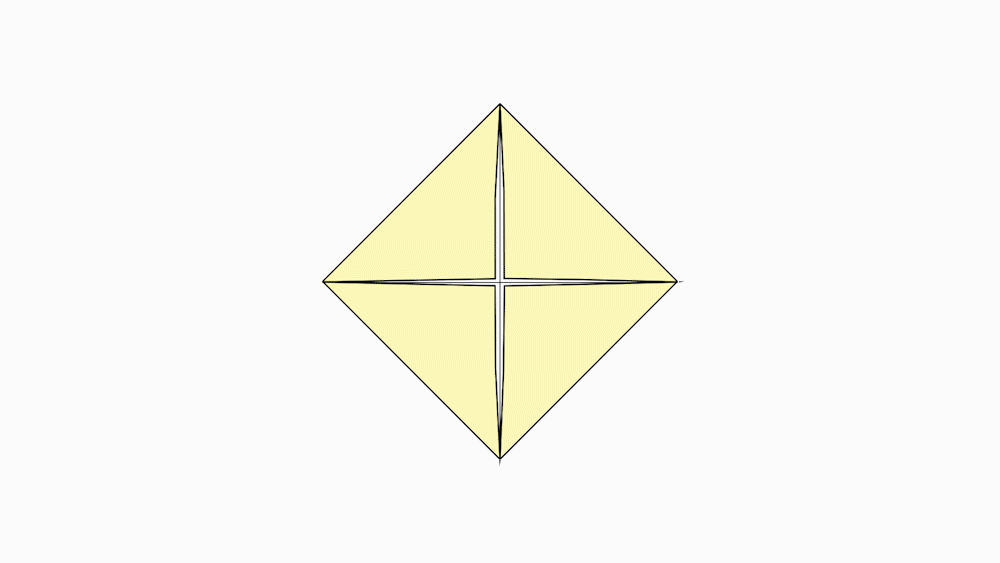
- הוראת קיפול: לפתוח בחזרה לריבוע (לקפל בנייר הגדול בלבד).
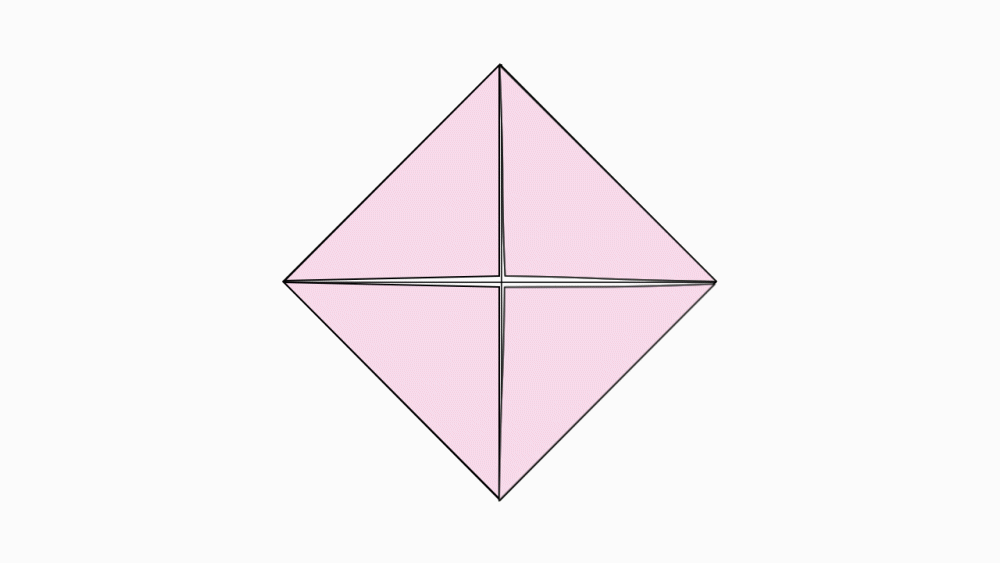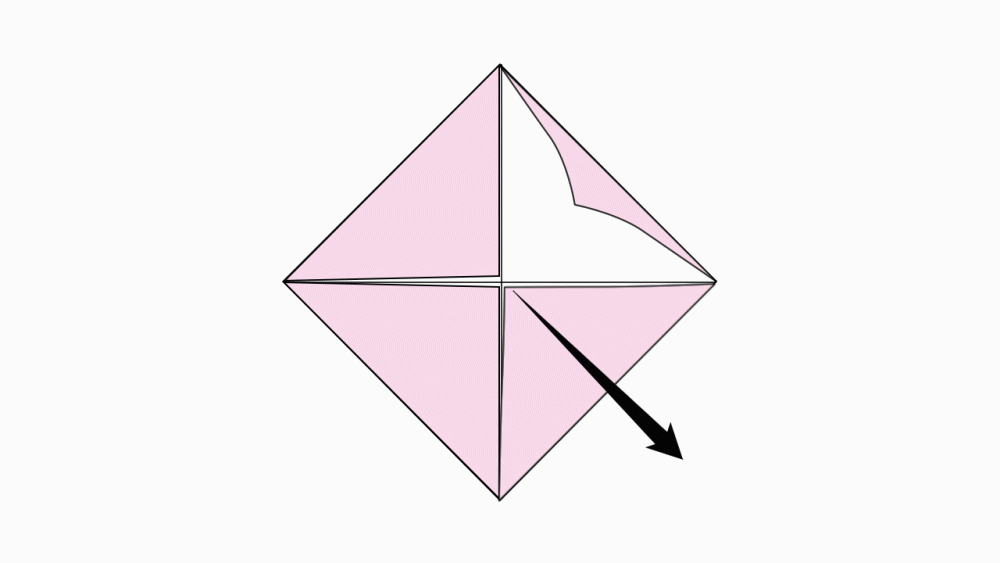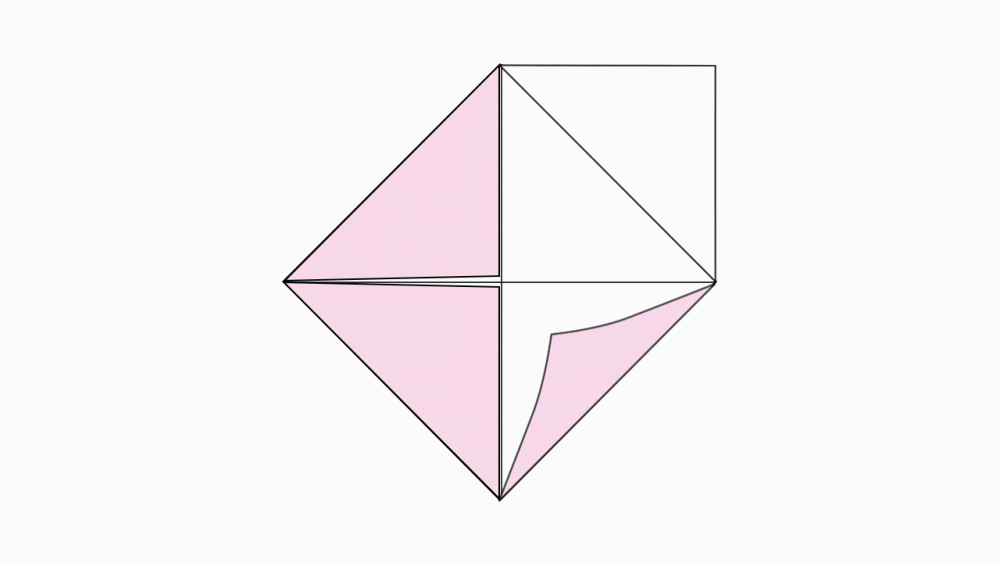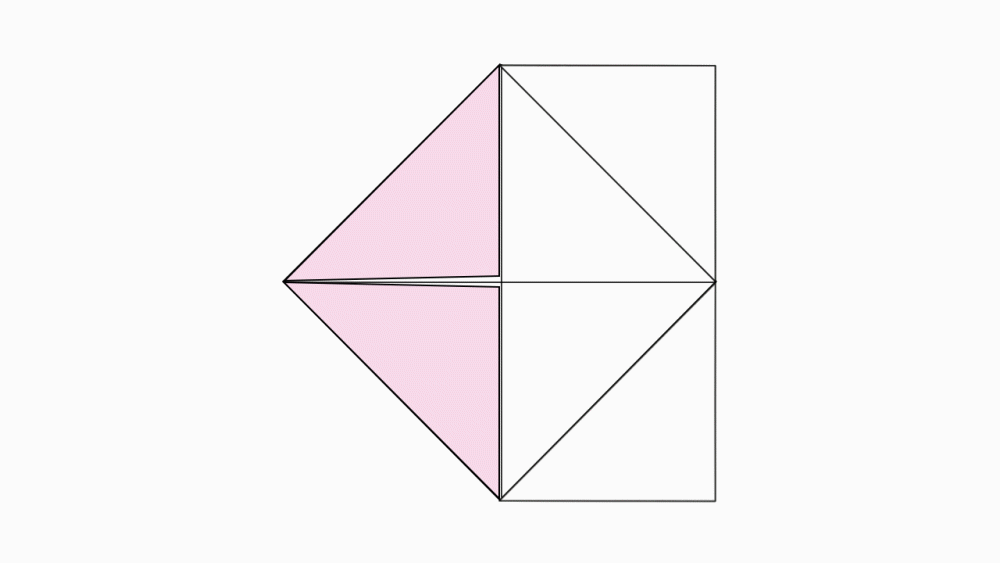
- הוראת קיפול: לקפל כל קדקוד לנקודת מפגש הישרים (לקפל בנייר הגדול בלבד).
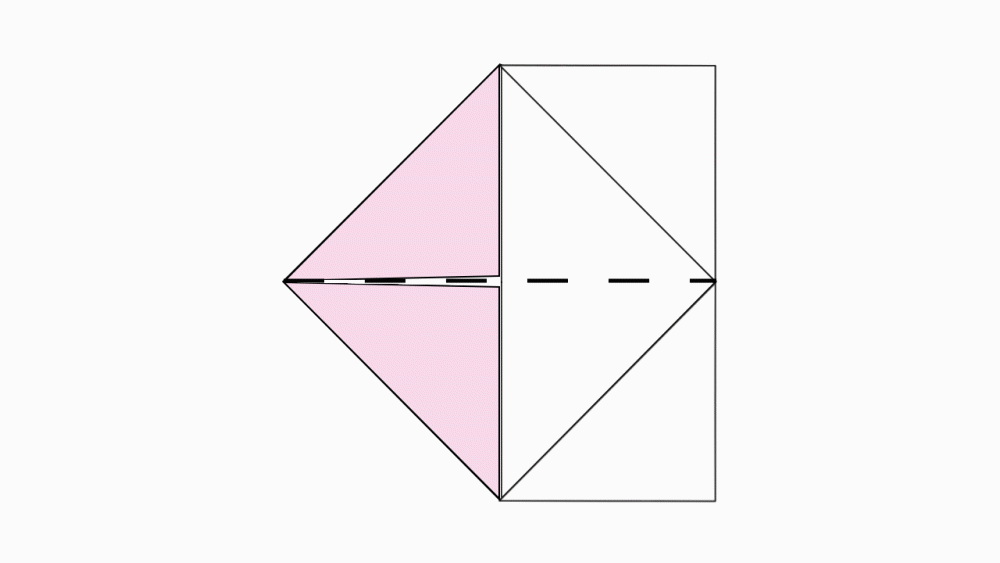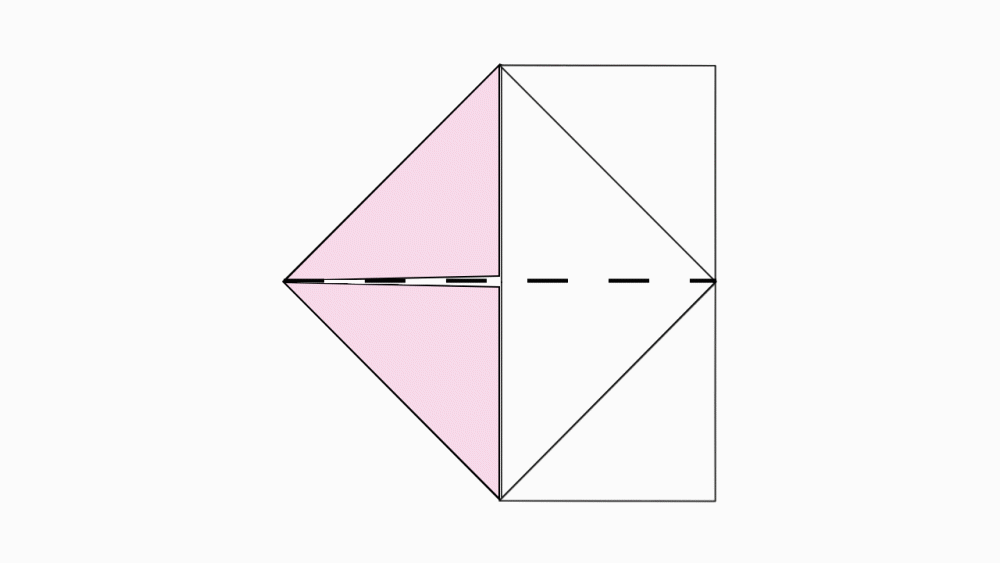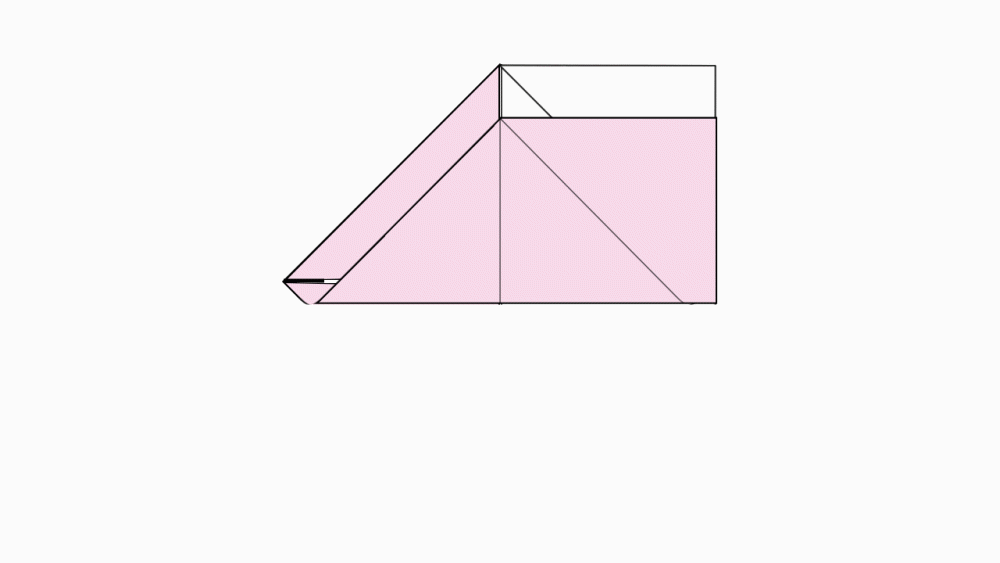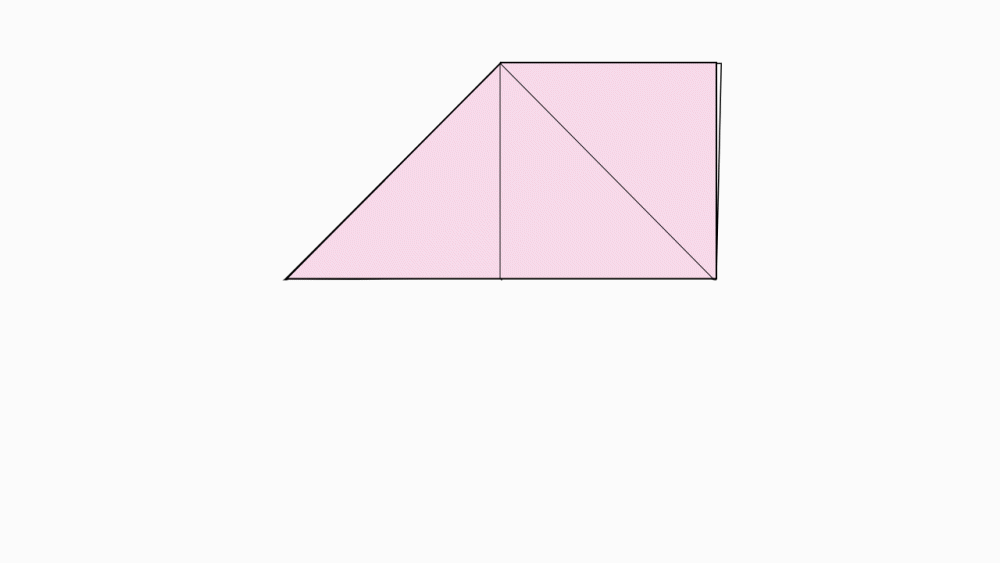
- הוראת קיפול: לפתוח את שני המשולשים.
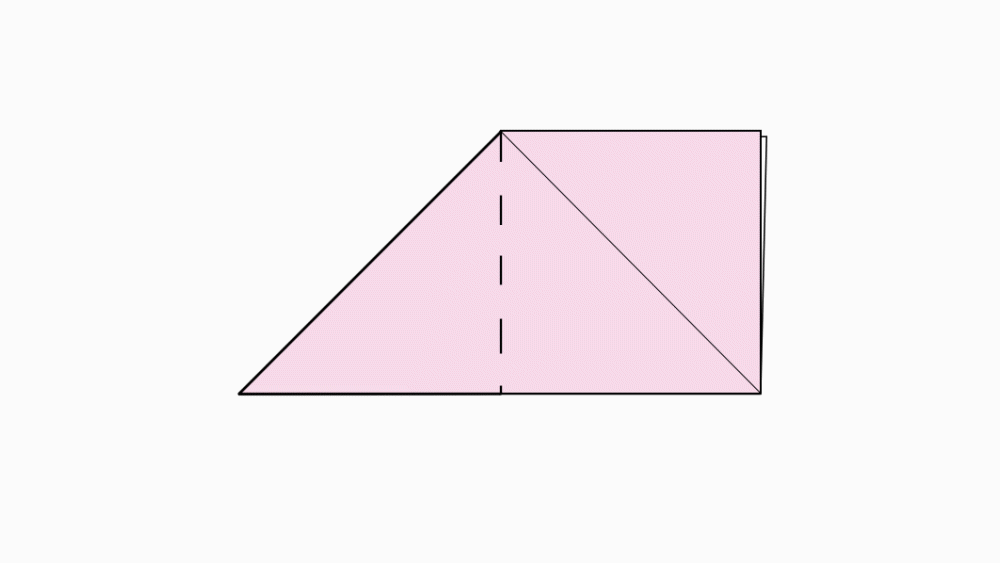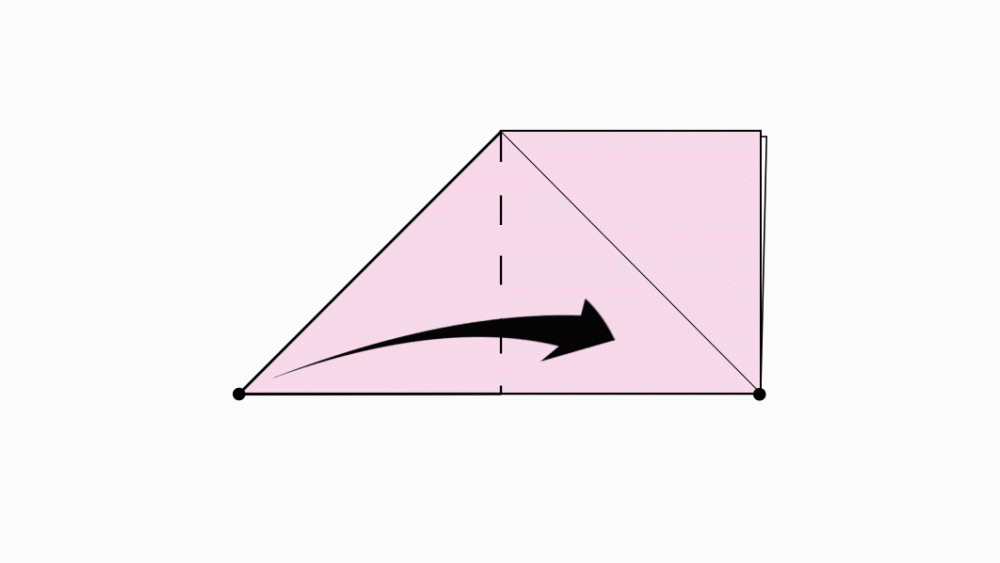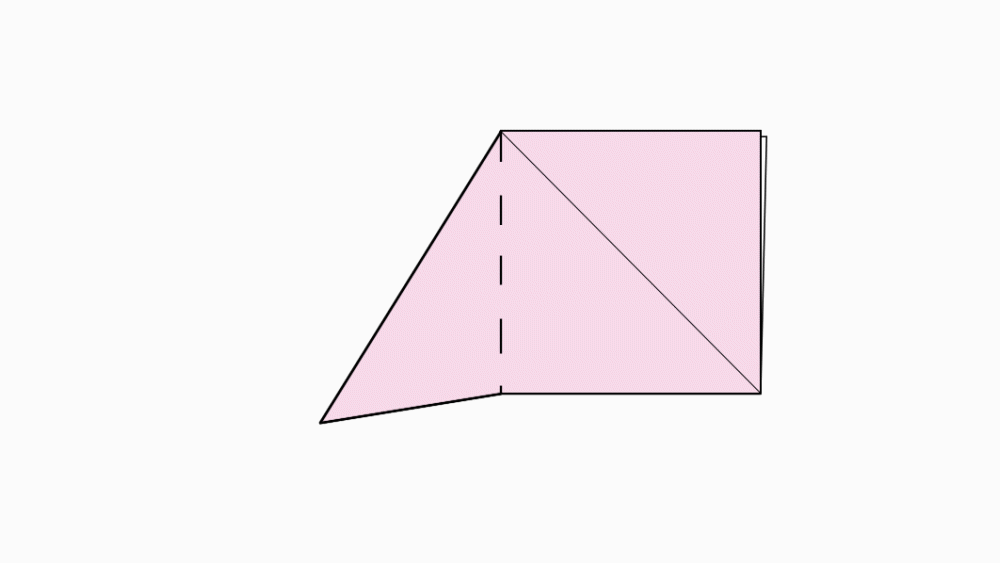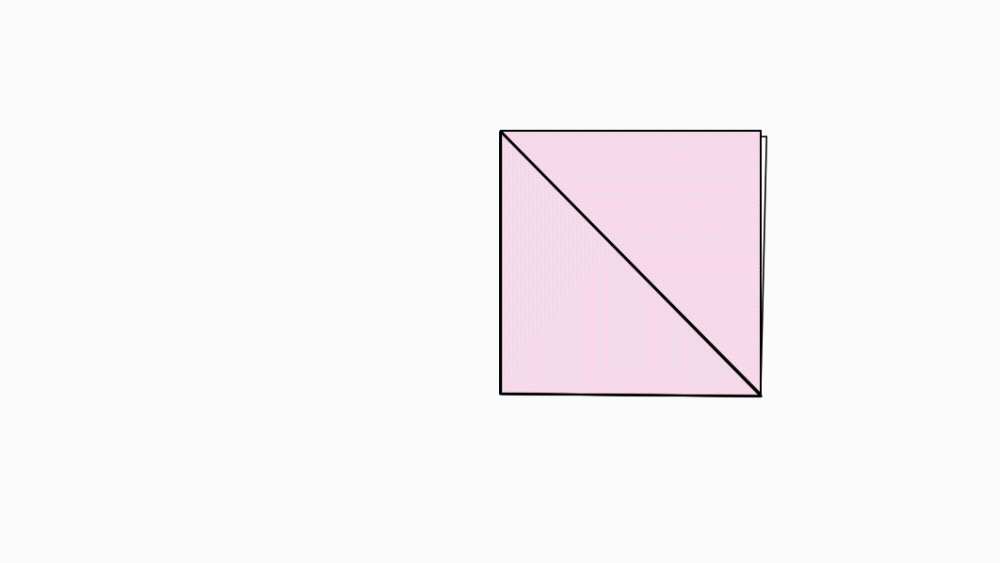
- הוראת קיפול: לקפל לשניים כך שיתקבל טרפז ישר זווית.
- הוראת קיפול: לקפל קדקוד לקדקוד, כפי שמודגם באנימציה.
- הוראת קיפול: להכניס משולש אחד אל הכיס. כפי שמודגם באנימציה.
- משימה בקבוצות: התחלקו לקבוצות. כל ארבעת תלמידים בקבוצה.
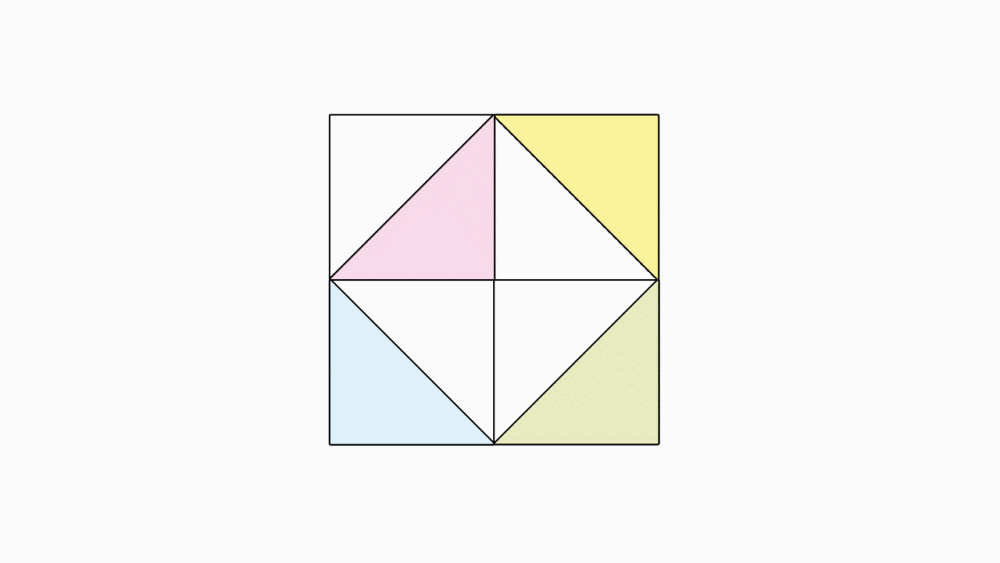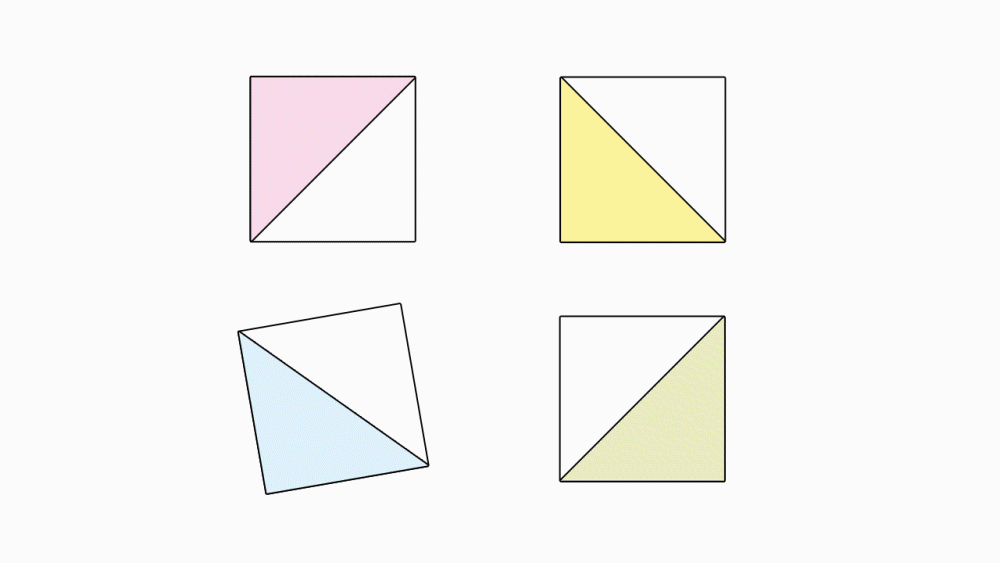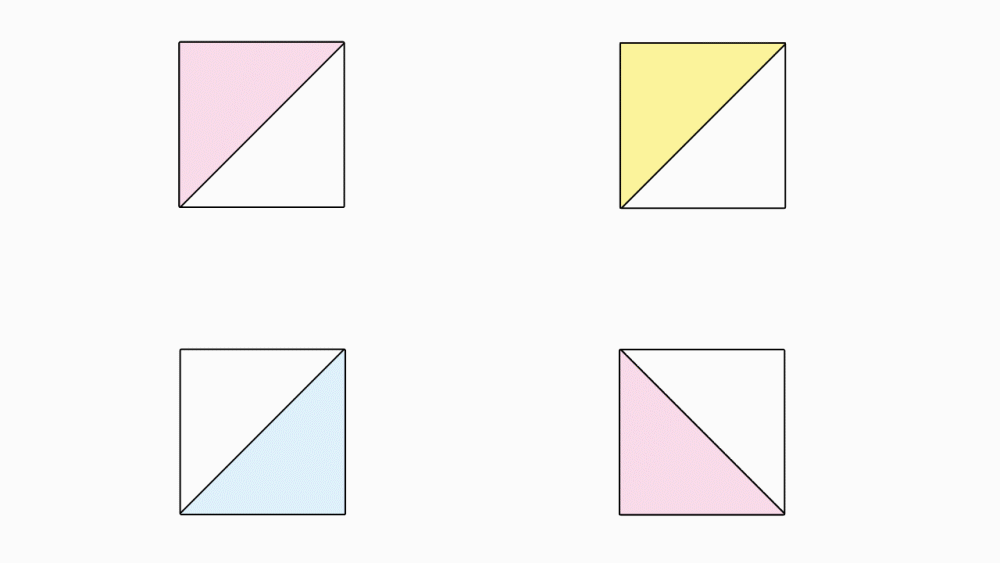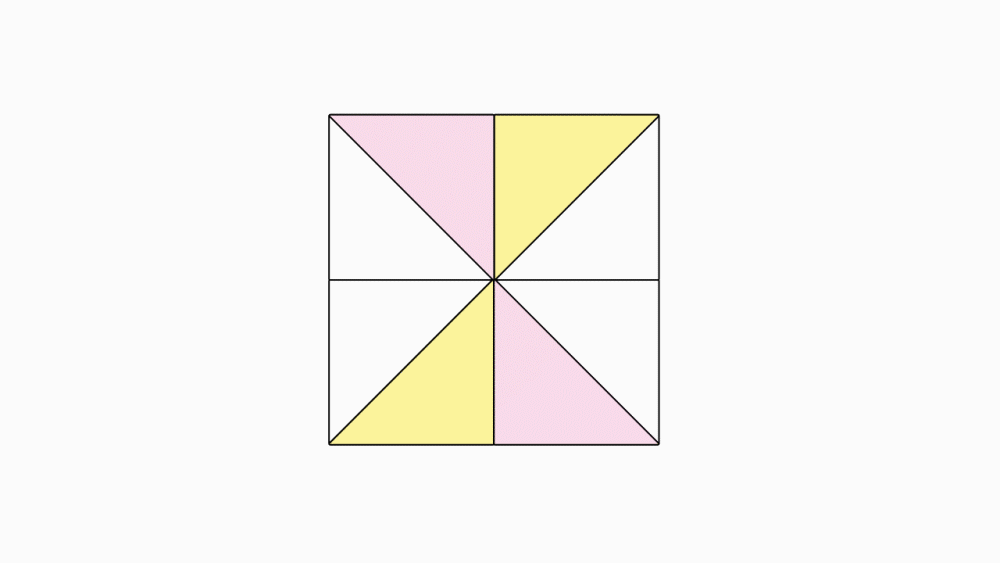
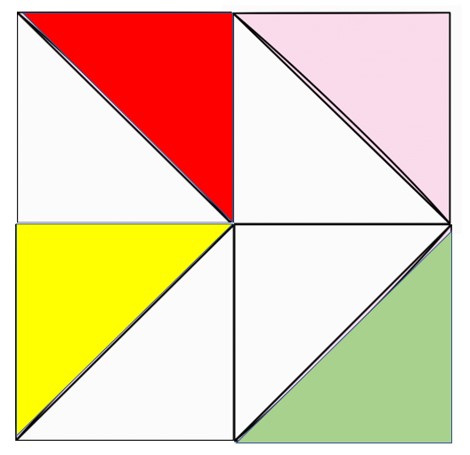
- משימה בקבוצות: האם תוכלו לסדר את החלקים שלכם כמו בדוגמה?
- קבוצות של 4 תלמידים.
- שאלה לדיון: איזה חלק מהשלם מייצגים המשולשים הצבעונים ביחד? ואיזה חלק מהשלם מייצגים המשולשים הלבנים ביחד? איזה חלק מהשלם משולש אחד צבעוני?
- הדגש כאן הוא על מושג המונה ללא התייחסות למיקום המשולשים (כאשר כל המשולשים חופפים ושווי שטח).
- תשובה1: שטח המשולשים הצבעונים ביחד הם חצי משטחו של השלם. גם שטח המשולשים הלבנים ביחד הם חצי משטחו של השלם.
- תשובה2: משולש אחד הוא $\dpi{120} \bg_white \bg_white \frac{1}{8}$ משטחו של השלם.
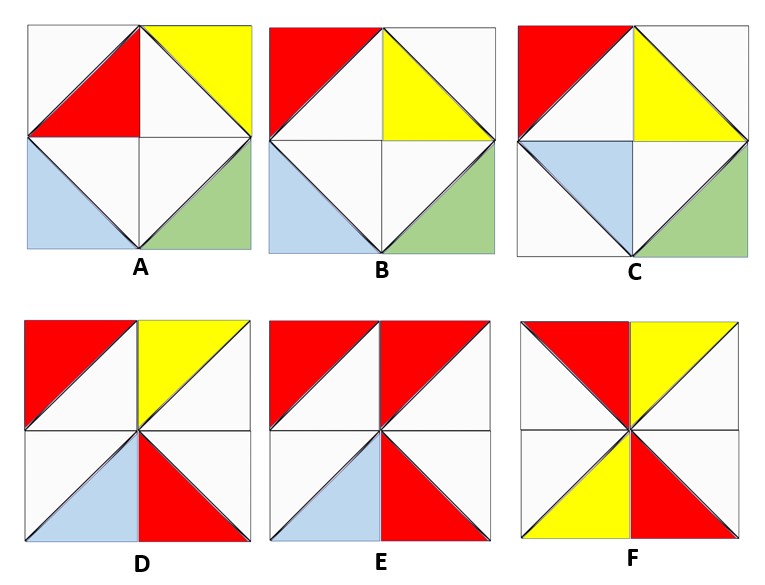
- משימה בקבוצות: הניחו כל 4 משולשים שקיפלתם כמו באיור. איזה חלק מהשלם מייצגים ביחד ארבעה משולשים.
- ניתן להזמין את התלמידים ללוח ולבקש שיציגו אפשרויות נוספות. בכל ייצוג להתייחס לחלק מהשלם מייצגים צירוף של משולשים צבעוניים או משולשים לבנים.
- תשובה1: שטח ארבעת המשולשים הצבעונים ביחד הם חצי משטחו של השלם. גם שטח של ארבעת המשולשים הלבנים ביחד הם חצי משטחו של השלם.
- בסיום פעילות זו על התלמיד להכיר ש 4/8= 1/2 ועל ידי הזזת המשולשים להראות את המצב של 4/8 מכסים חצי הנייר השלם לעומת החצי השני עם 4 משולשים לבנים.
- תשובה2: משולש אחד הוא $\dpi{150} \bg_white \bg_white \frac{1}{8}$ משטחו של השלם.
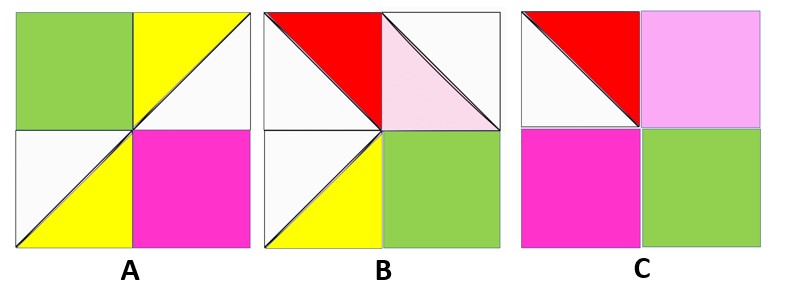
- משימה בקבוצות: הניחו כל ארבעה ריבועים שקיפלתם כפי שמודגם (חלקם מהצד עם המשולשים וחלק מהצד של הריבוע), ובחנו איזה חלק מהשלם הריבועים הקטנים?
- קבוצות של 4 תלמידים. רוצים להדגיש במקום זה שלא חייבים לשים כל צורה צמודה לצורה השנייה
- תשובה: בריבוע המסומן באות A הריבועים הקטנים הם חצי משטחו של הריבוע השלם. בריבוע המסומן באות B הריבוע הקטן הוא רבע משטחו של הריבוע השלם. בריבוע המסומן באות C הריבועים הקטנים הם שלושת רבעים משטחו של הריבוע השלם.
- כאן המקום להתייחס לחלק הלא צבעוני בכל ריבוע. איך נבטא את הלבנים כחלק מהשלם. בריבוע A החלק הלבן הוא 1/4 (3/4+ 1/4=1). בריבוע B החלק הלבן הוא 3/8 (1/4+ 3/8+3/8 =1)
- הוראת קיפול: לקפל את המשולש הלבן פנימה אל הכיס כפי שמודגם באנימציה.
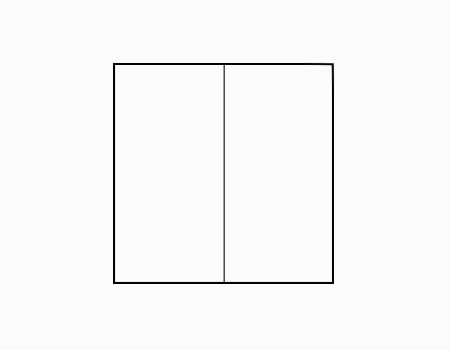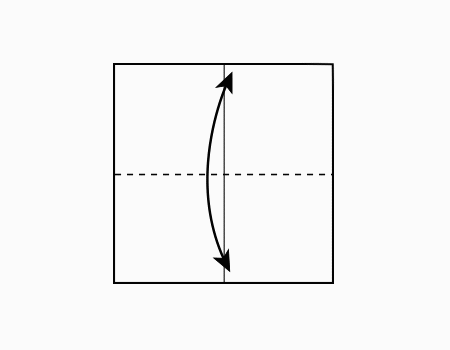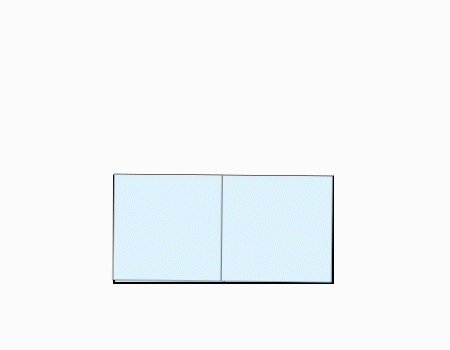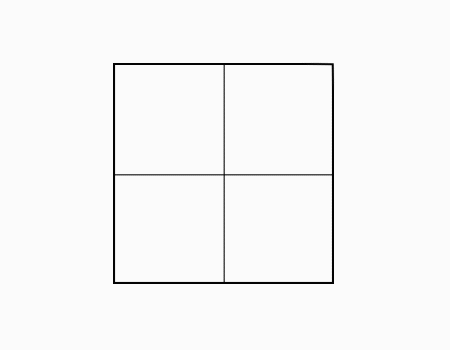
- הוראת קיפול: לקפל בשני הניירות הקטנים, צלע לצלע מקבילה ולפתוח.
- הוראת קיפול: לקפל בשני הניירות הקטנים צלע לצלע מקבילה ולפתוח.
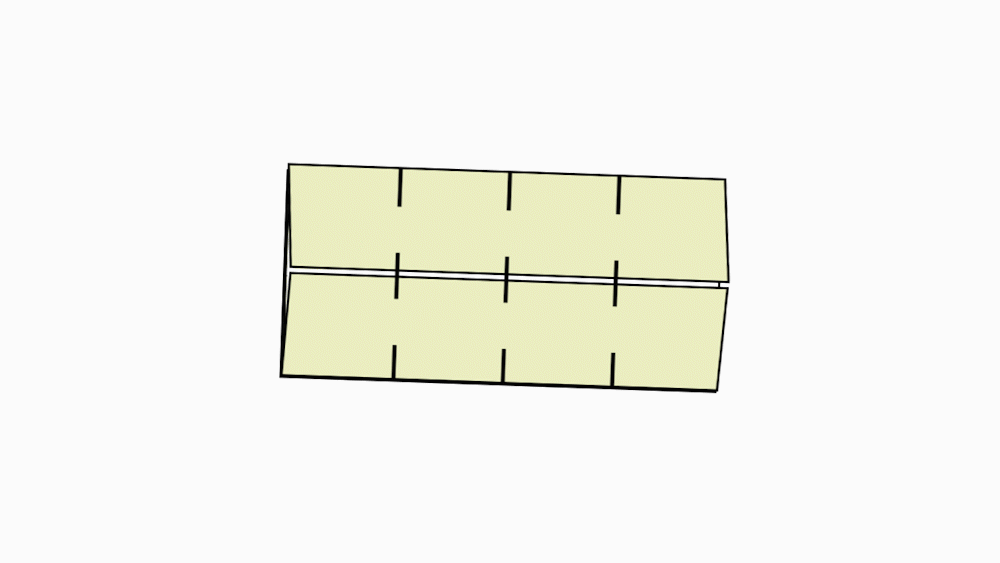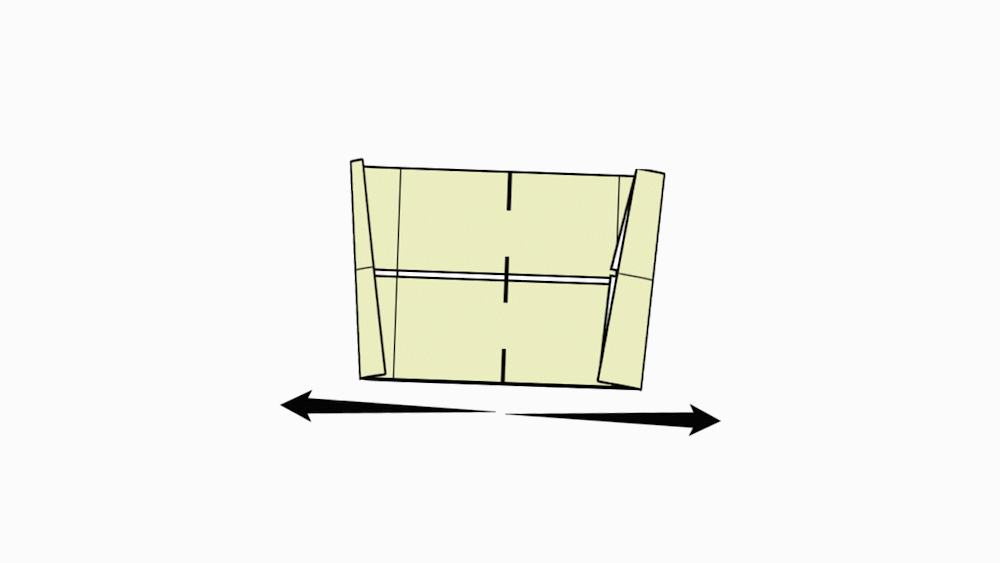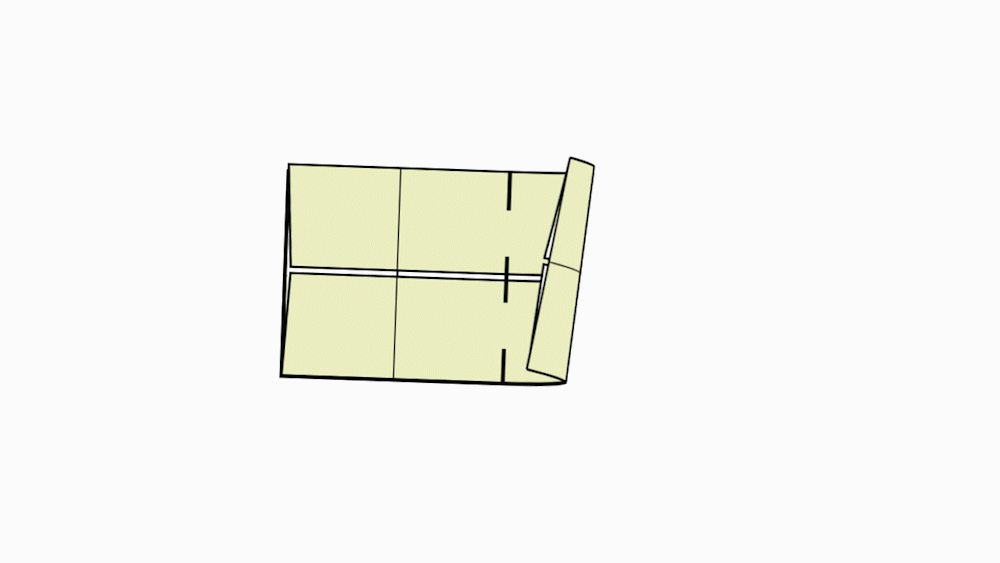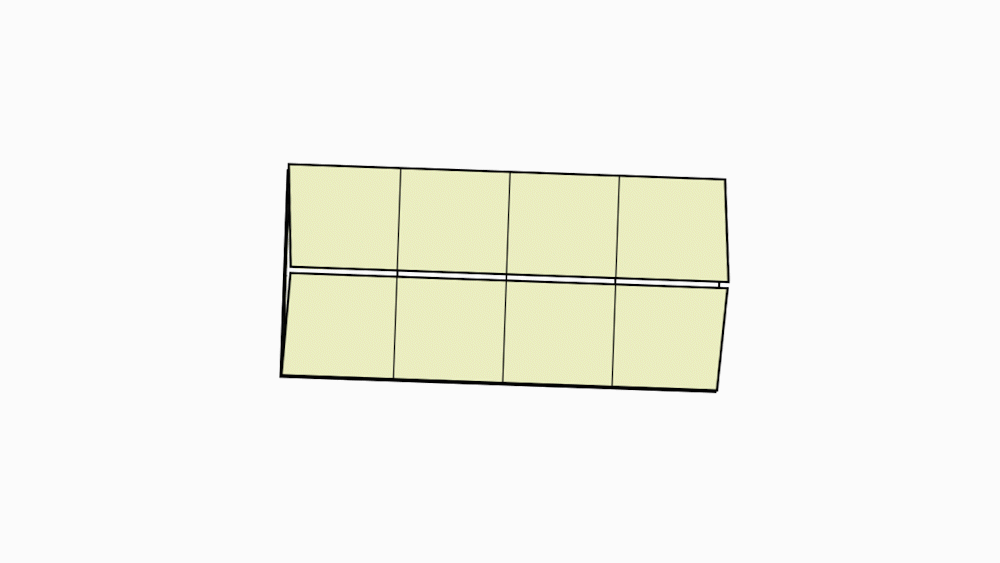
- הוראת קיפול: לקפל בשני הניירות הקטנים כל צלע לקו הסימטריה ולפתוח.
- הוראת קיפול: בשני הניירות הקטנים. לקפל בחזרה כל צלע לקו הסימטריה.
- הוראת קיפול: בשני הניירות הקטנים.לקפל כל צלע קצרה לקו הסימטריה.
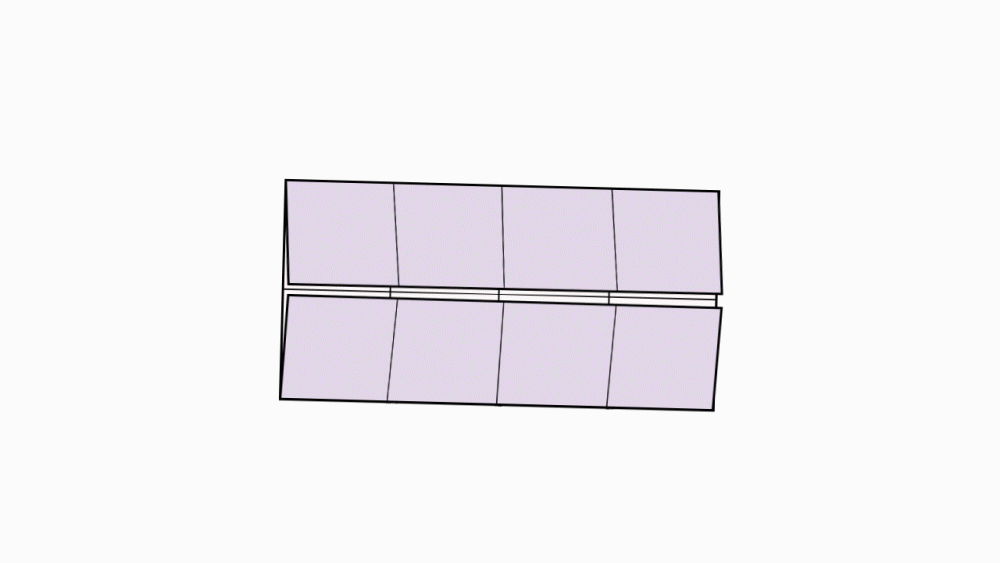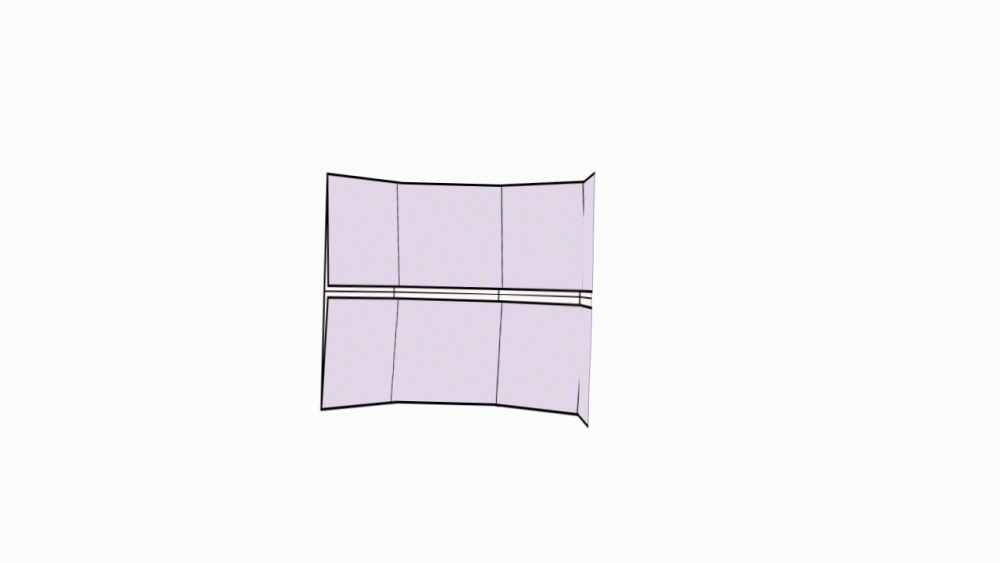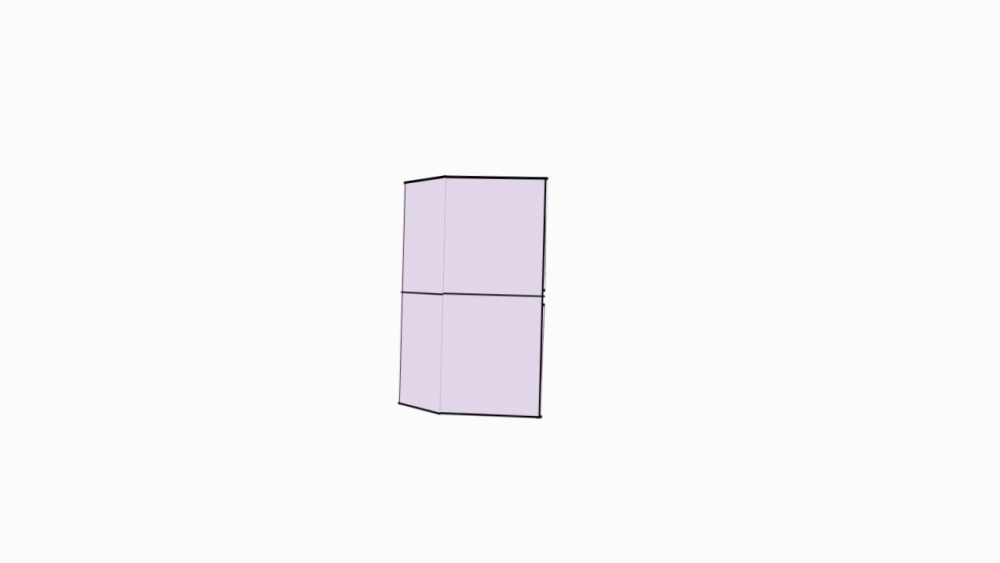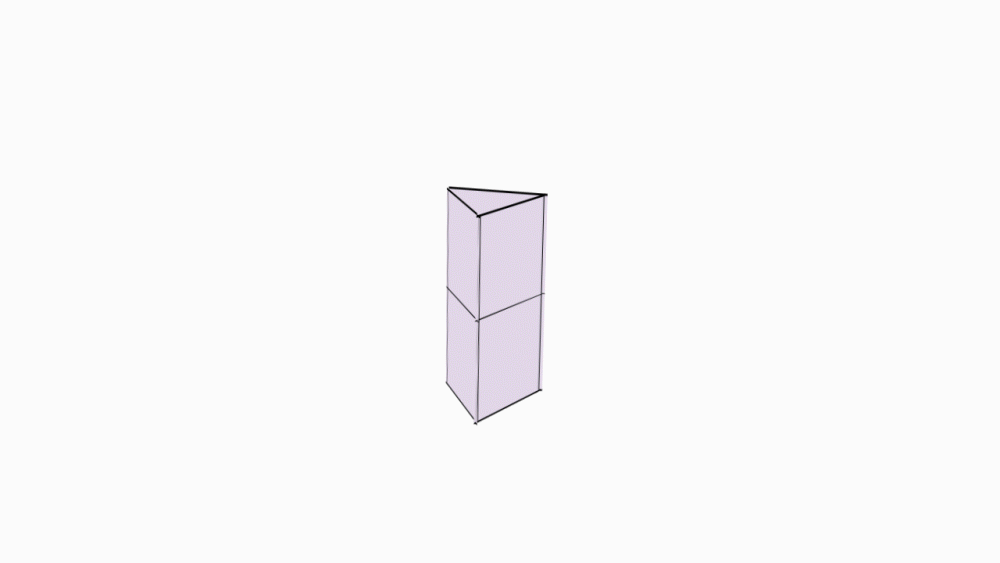
- הוראת קיפול: בשני הניירות הקטנים.להכניס צלע אל צלע, כך שתקבל מעטפת מנסרה משולשת.
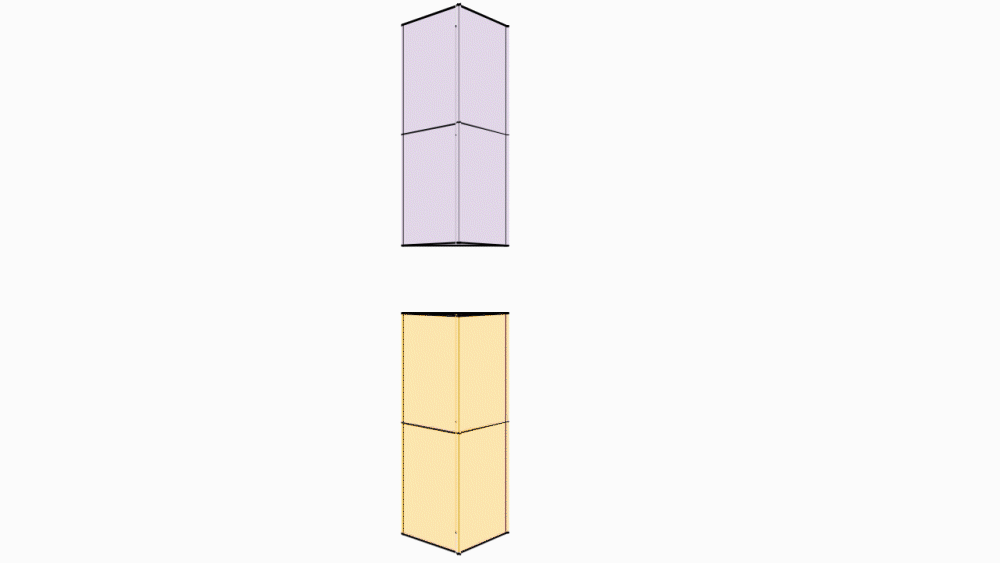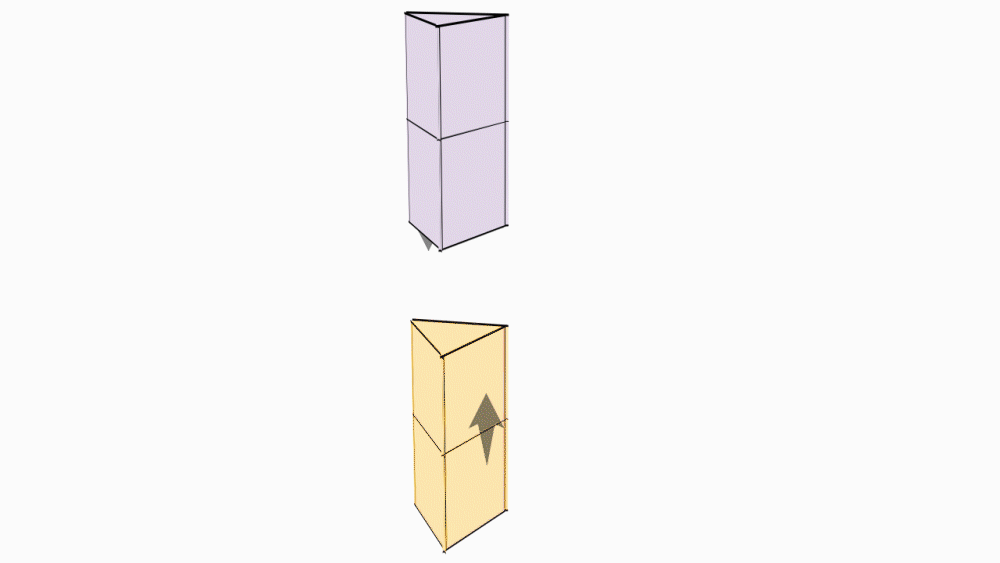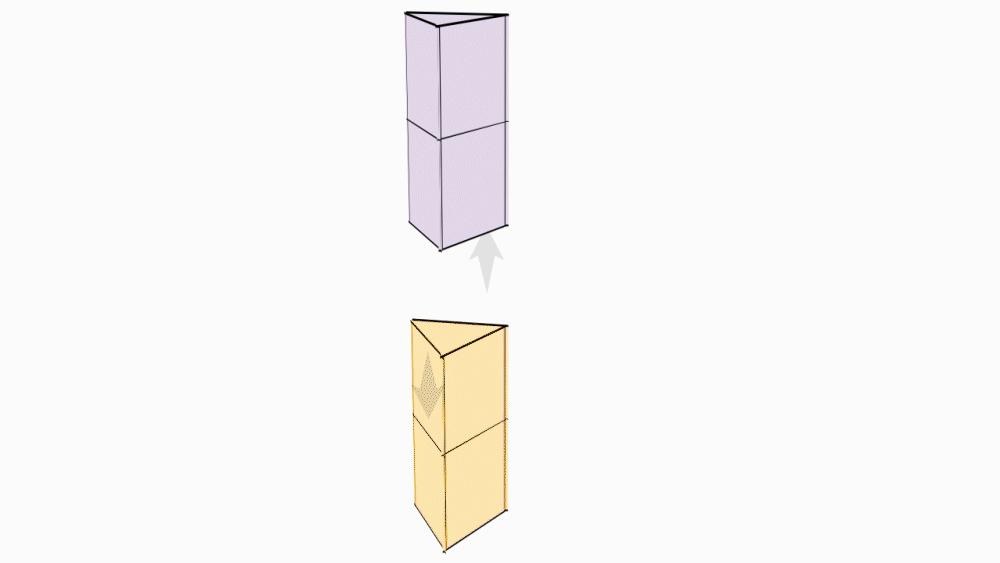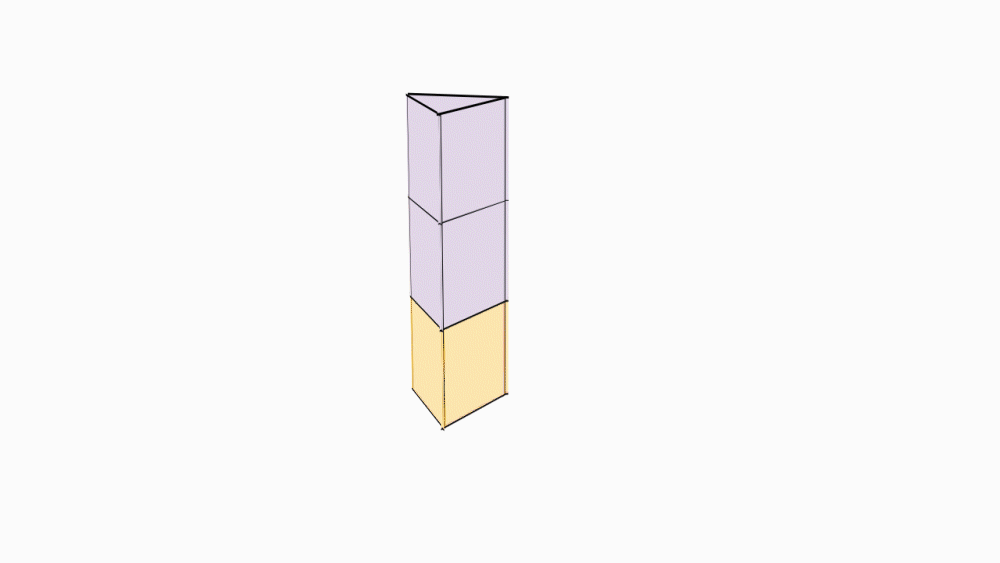
- הוראת קיפול: ליצירת גזע העץ, נכניס מעטפת מנסרה אחת אל השניה.
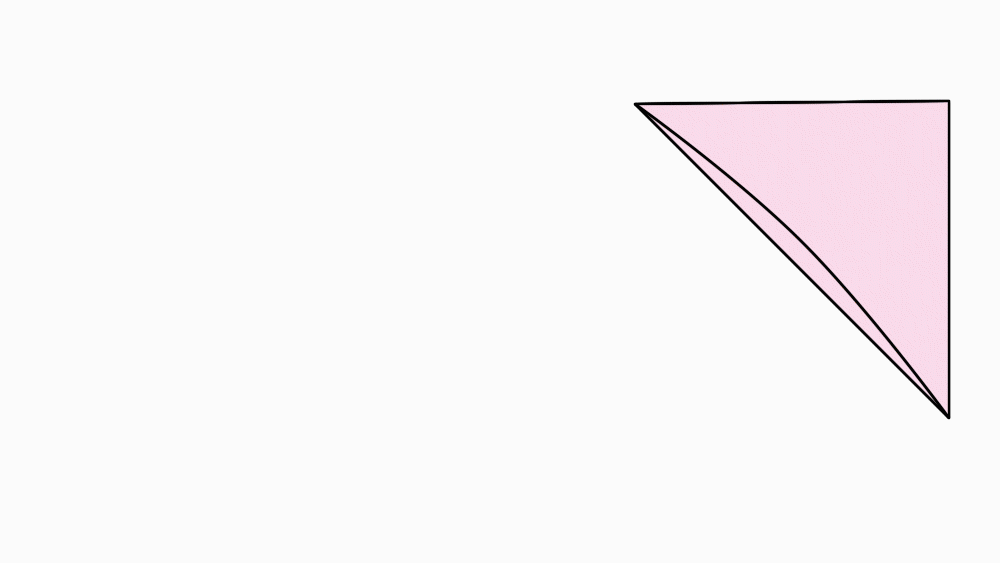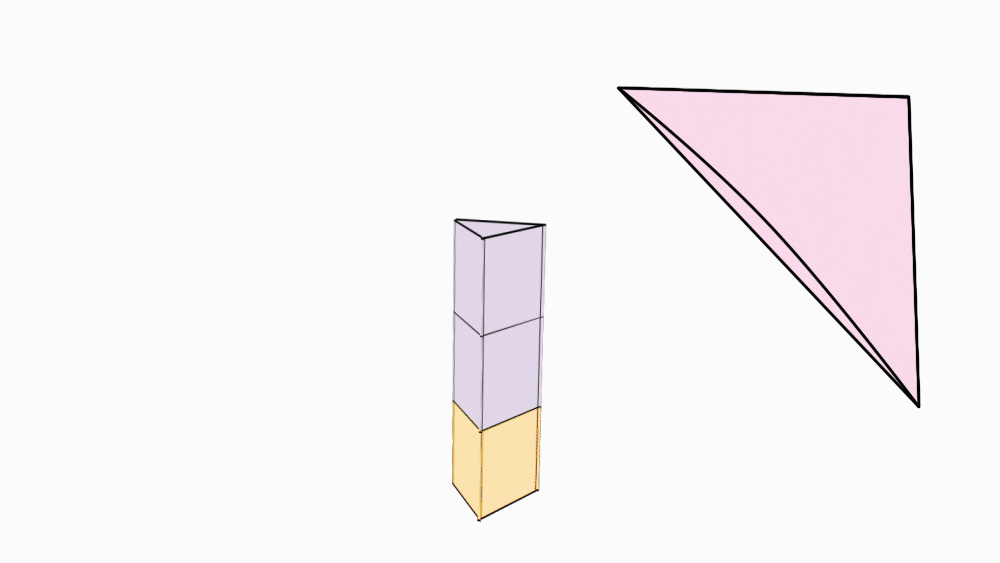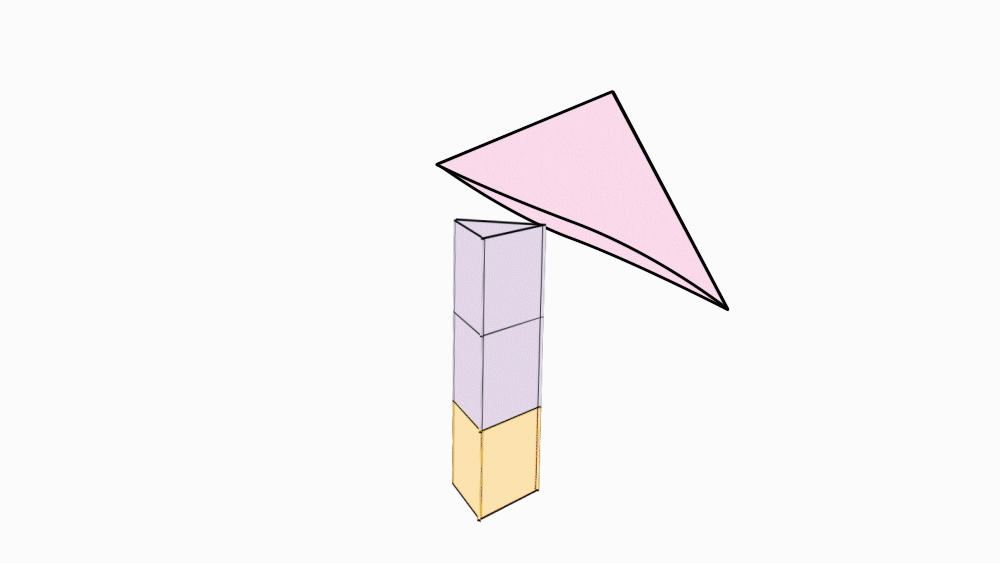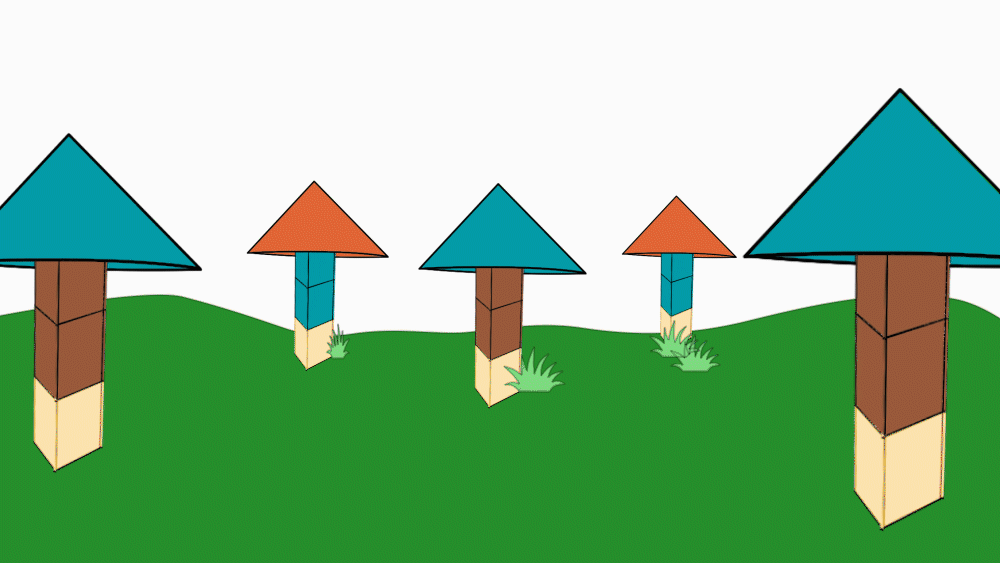
- הוראת קיפול: נחבר את חלקי העץ.
- הוראת קיפול: שימו לב שניתן ליצור עצים שונים.

מטרת הפעילות
- הכרת השברים היסודיים באמצעות מודל השטח.
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.
- זיהו ורישום חלקי השלם במודל השטח ולא רק שברים יסודיים (המונה אינו 1)

שם הדגם
עץ.

מספר סידורי: 4050/3

שם היוצר/ת
מירי גולן

© כל הזכויות שמורות למרכז הישראלי לאוריגאמי

רצף מומלץ
שיעור חלק מהשלם 1/5 חלק ג הוא חלק מהסדרה של השיעורים בנושא השלם.
השיעור הבא יהיה חלק מהשלם 2/5

מומלץ ללמד לפי הרצף המופיע באתר (בהתאם לתכנית הלימודים).

על השיעור
התלמידים יקפלו שני ניירות בגודל 15 ס”מ
התלמידים יחקרו את החלקים מתוך השלם.

פעילות זו היא תשתית עבור הוראת שברים בהמשך.

.

משך זמן פעילות מומלץ: 45 דקות

* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.

ציוני דרך
כיתה ד – עמוד 1

מילון מונחים בגאומטריה

הדגשים בהוראת השבר כחלק משלם:
1. קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
2. החלקים לא חייבים להיות חופפים.
3. כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
4. חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
5. כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
6. השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול משטחו של שלושה רבעים של ריבוע קטן.

חומרים
נייר אחד בגודל 15ס”מ/ 15ס”מ ושני ניירות בגודל של 9/9 ס”מ

משוב מעמיתים

שדה חובה*

You must be logged in to post a comment.