Sorry, you have Javascript Disabled! To see this page as it is meant to appear, please enable your Javascript! See instructions here

משפט פיתגורס: הוכחות גיאומטריות והוכחות אלגבראיות עם קיפולי נייר

משפט פיתגורס: הוכחות גיאומטריות והוכחות אלגבראיות עם קיפולי נייר

משפט פיתגורס: הוכחות גיאומטריות והוכחות אלגבראיות עם קיפולי נייר

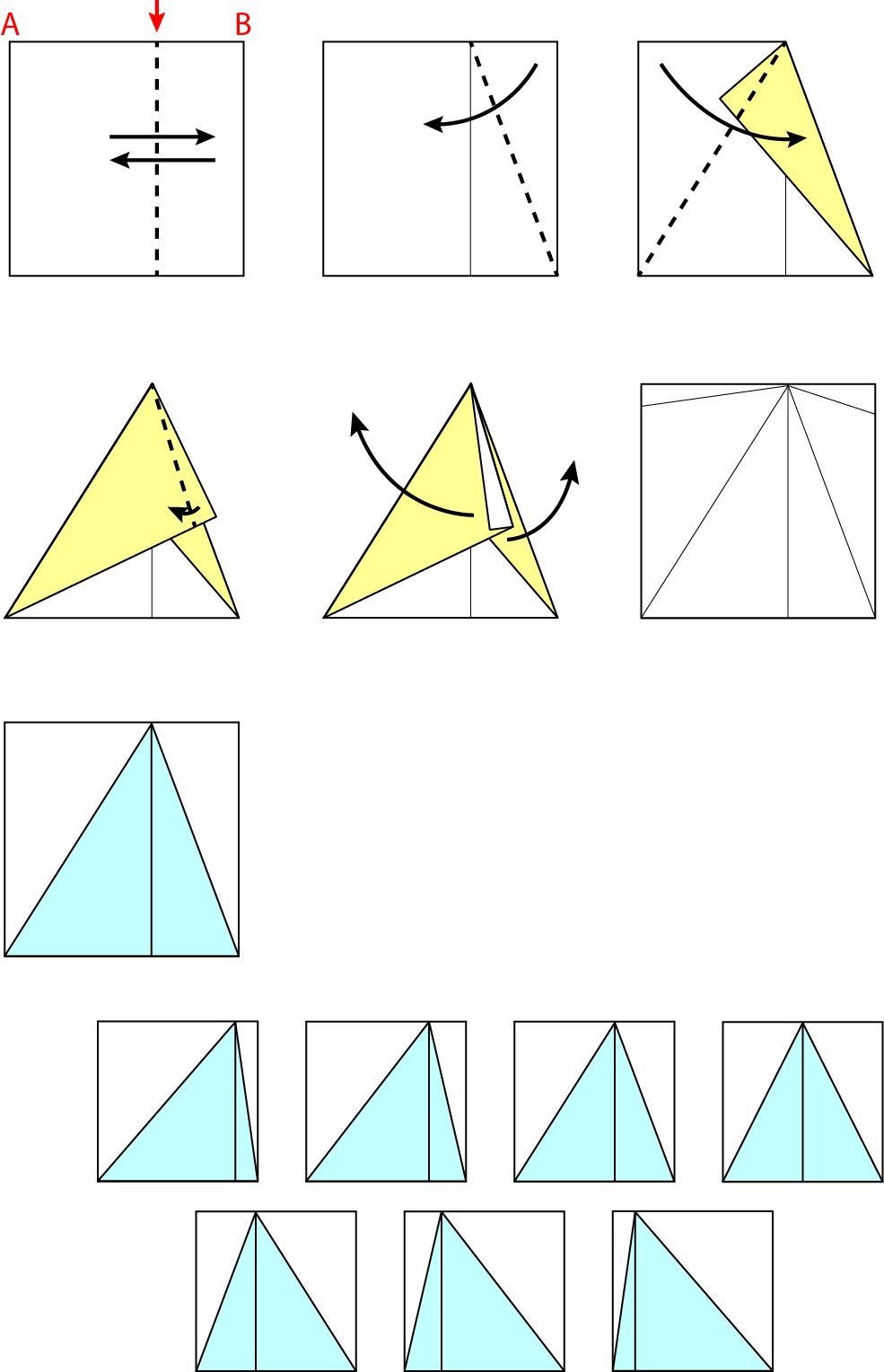
- בחרו נייר 1 ממניפת הצבעים.
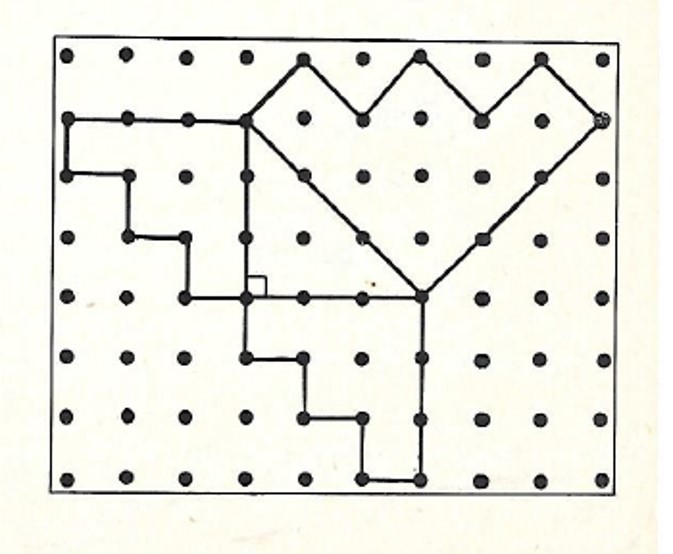
- שאלה לדיון: קפלו את הנייר על פי בחירתכם לחצי מהריבוע והוכיחו שהנייר אכן הוא חציו של הריבוע.
- בשלב זה ניתן לתלמידים לקפל באופן חופשי, ולהסביר מדוע הם חושבים שהקיפול שלהם הוא חציו של הריבוע. ולראות את ההבדלים בין הקיפול של התלמידים.
- הקיפול הבא בנייר 1 ממניפת הצבעים.
- הוראת קיפול: להניח נייר נוסף כשהצד הצבעוני פונה אליכם ולקפל למלבן לבן.
- הוראת קיפול: לקפל את הצלע הארוכה של המלבן אל הצלע המקבילה.
- הוראת קיפול: להפוך לצד השני.
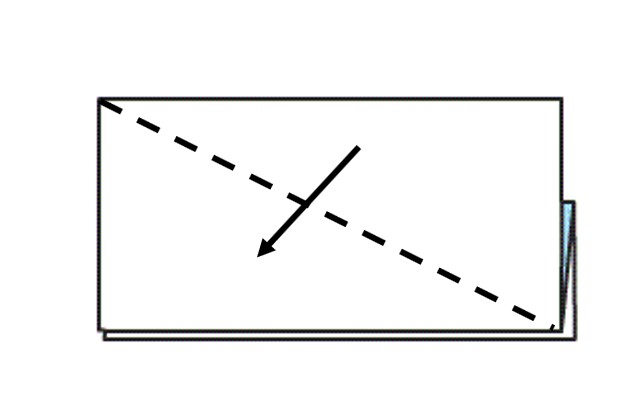
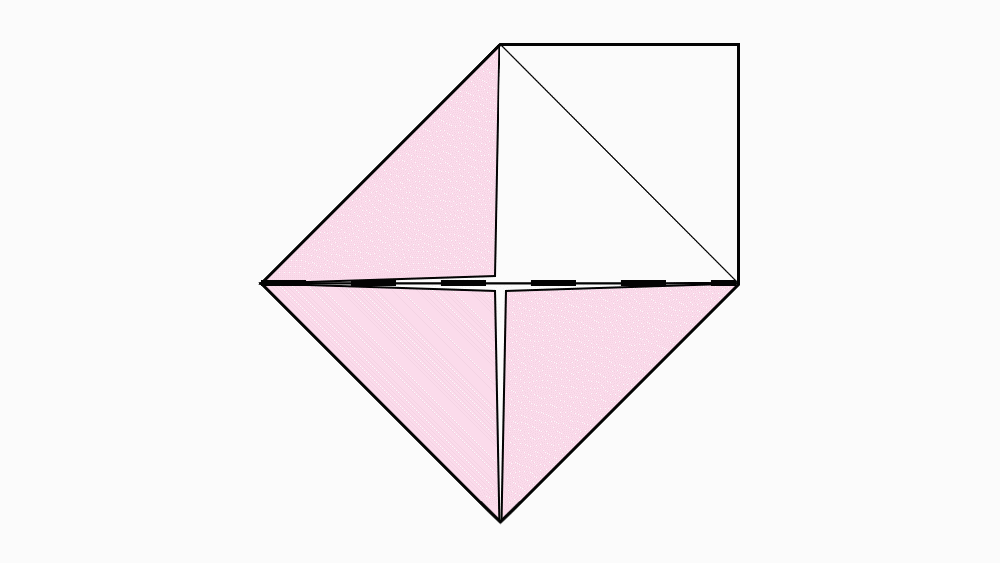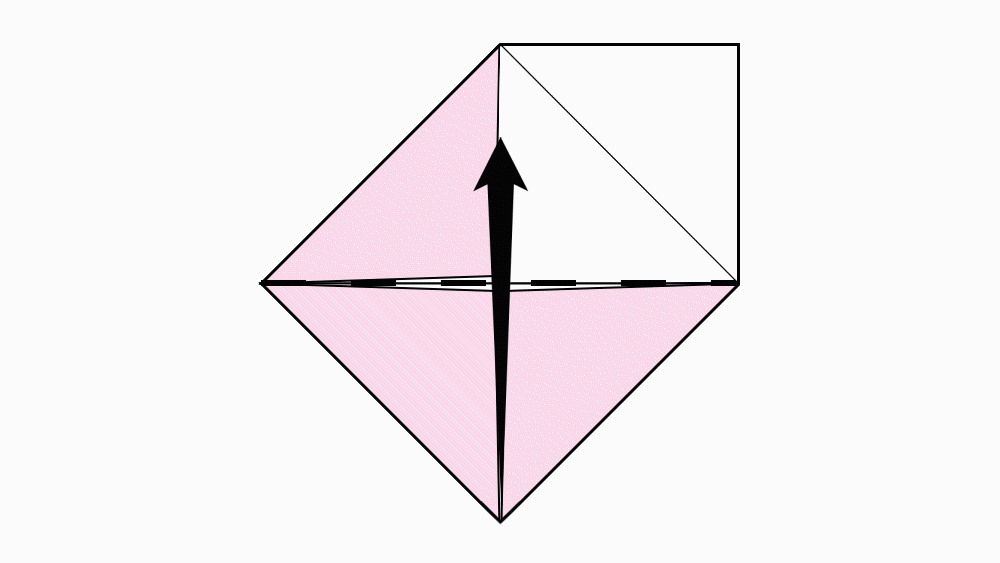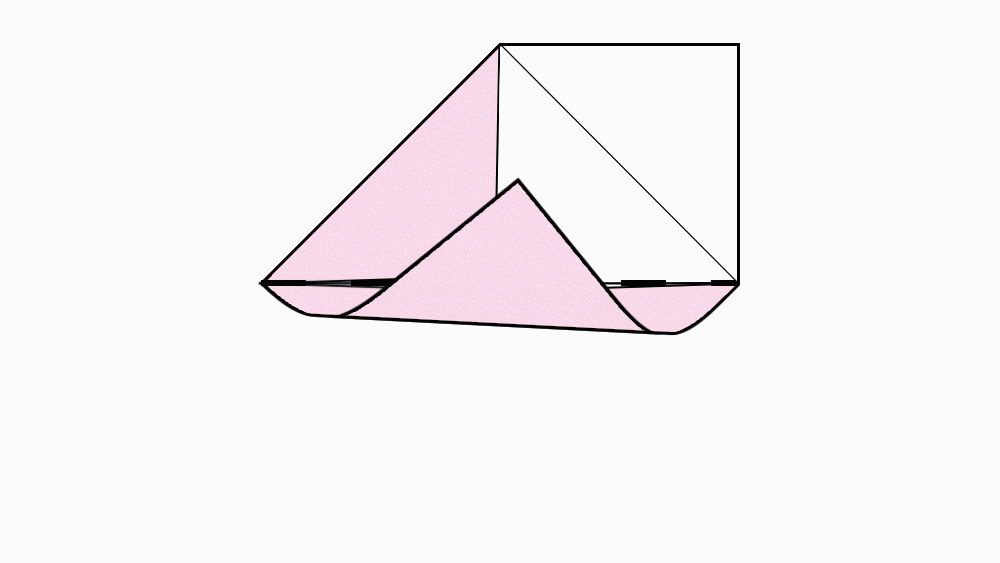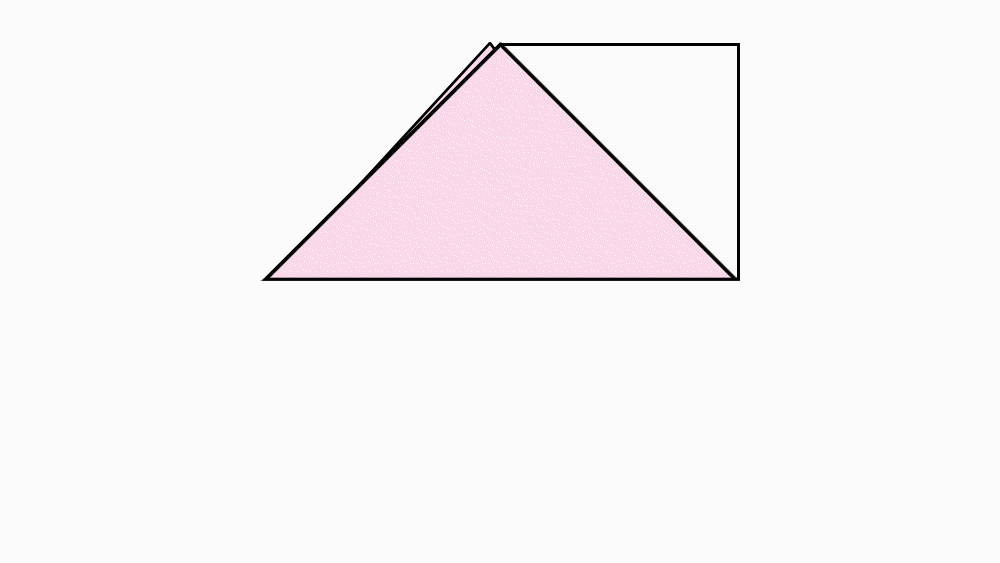
- הוראת קיפול: לקפל לפי הסימון את האלכסון של המלבן, ופיתחו את הקיפולים.
- שאלה לדיון: מהו היחס של שטחי הנייר המקופל, לשטח הריבוע לפני הקיפול.
- שאלה לדיון: האם ניתן לומר ששטחם של המשולש והמלבן ביחד הוא חצי משטחו של הריבוע? הסבירו
- הקיפול הבא בנייר 1 ממניפת הצבעים.
- הוראת קיפול: לקפל בנייר נוסף, צלע לצלע מקבילה ולפתוח.
- הוראת קיפול: לקפל צלע קצרה לצלע מקבילה ולפתוח לריבוע.
- הוראת קיפול: לקפל את שני הקדקודים למשולשים לפי הסימון באנימציה.
- הוראת קיפול: לקפל לפי הסימון את הצלע של המלבן הלבן לצלע המקבילה.
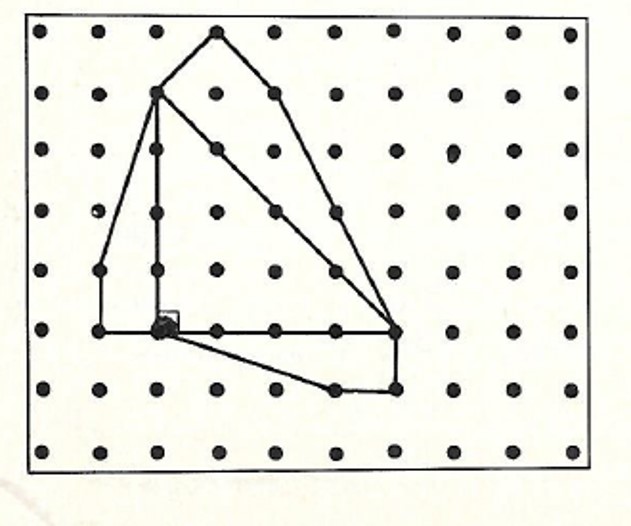
- שאלה לדיון: פיתחו את הקיפולים בנייר אחד בלבד ובחנו, מהו היחס של שטחי הנייר המקופל, לשטח הריבוע לפני הקיפול.
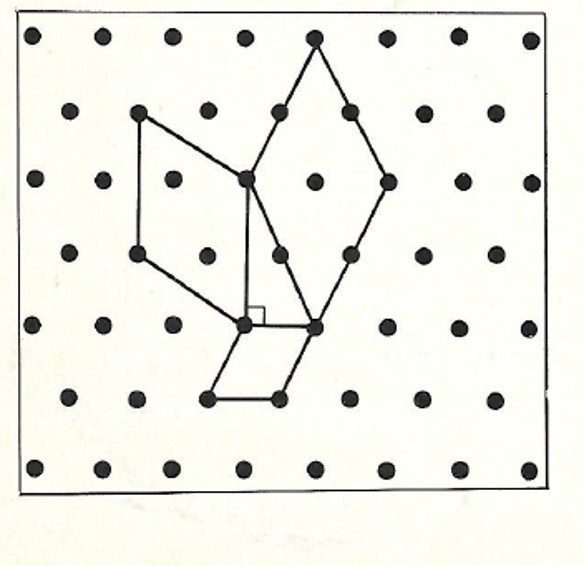
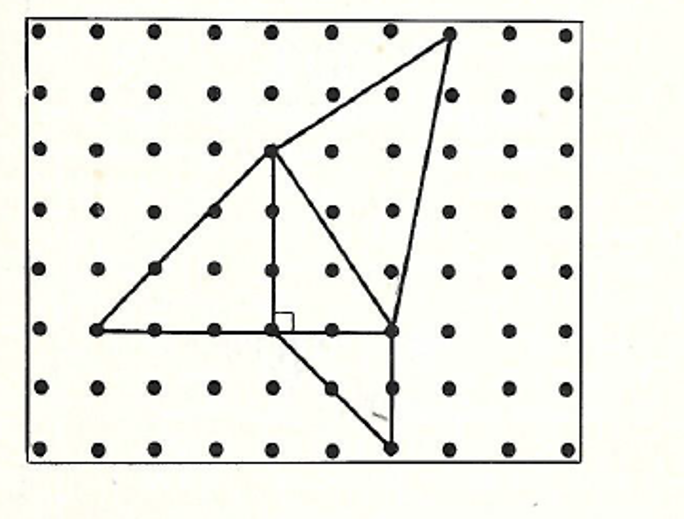
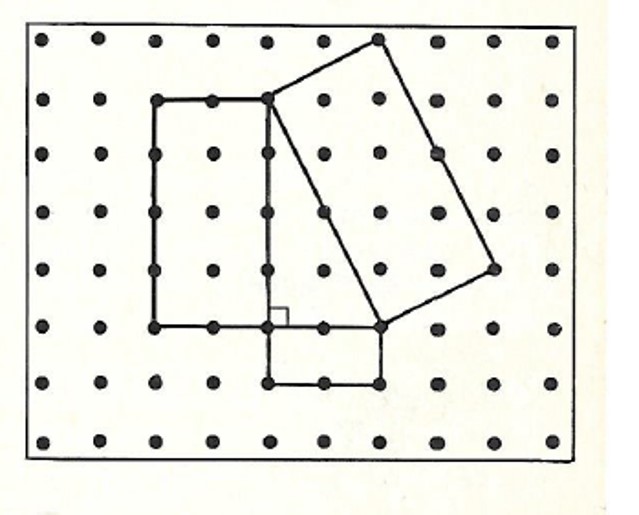
- שאלה לדיון: מה ניתן לומר על האיור שלפניכם?הסבירו
- כל תלמיד יבחר 11 דפים ממניפת הניירות.
- מומלץ לתת לתלמידים לעבוד בקבוצות עבודה.
- הוראת קיפול: קפלו כך שיתקבלו שני מלבנים שווים בשטחם. (לקפל בכל הניירות).
- הוראת קיפול: קפלו כך שיתקבלו ארבעה ריבועים שווים בשטחם. (לקפל בכל הניירות).
- הוראת קיפול: פיתחו בחזרה למלבן. (לקפל בכל הניירות).
- הוראת קיפול: פיתחו בחזרה לריבוע. (בכל הניירות).
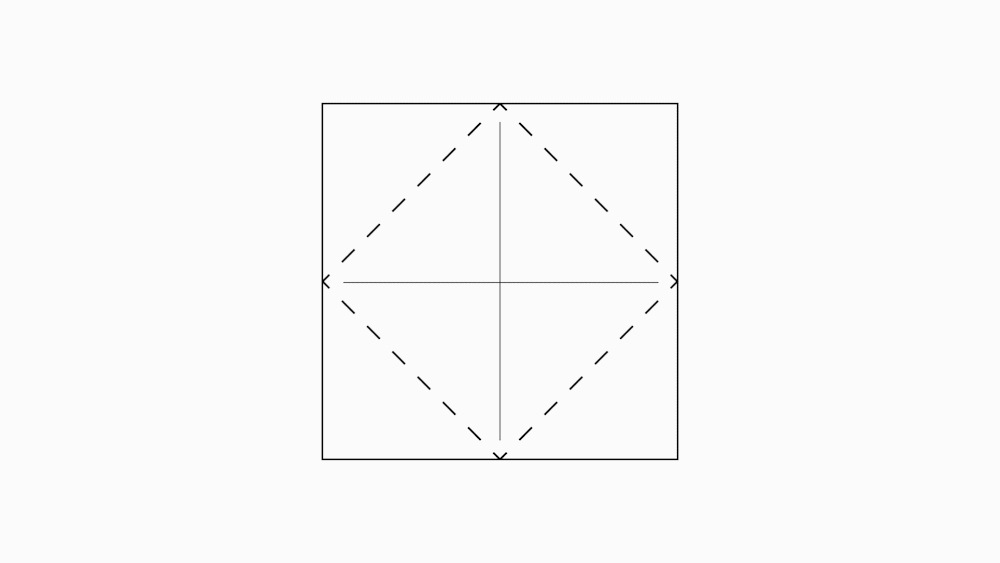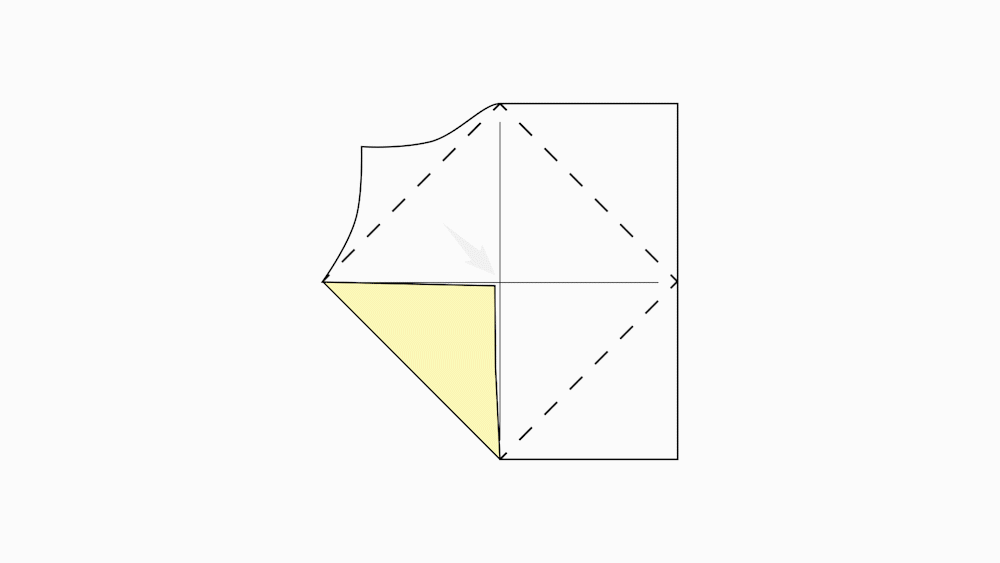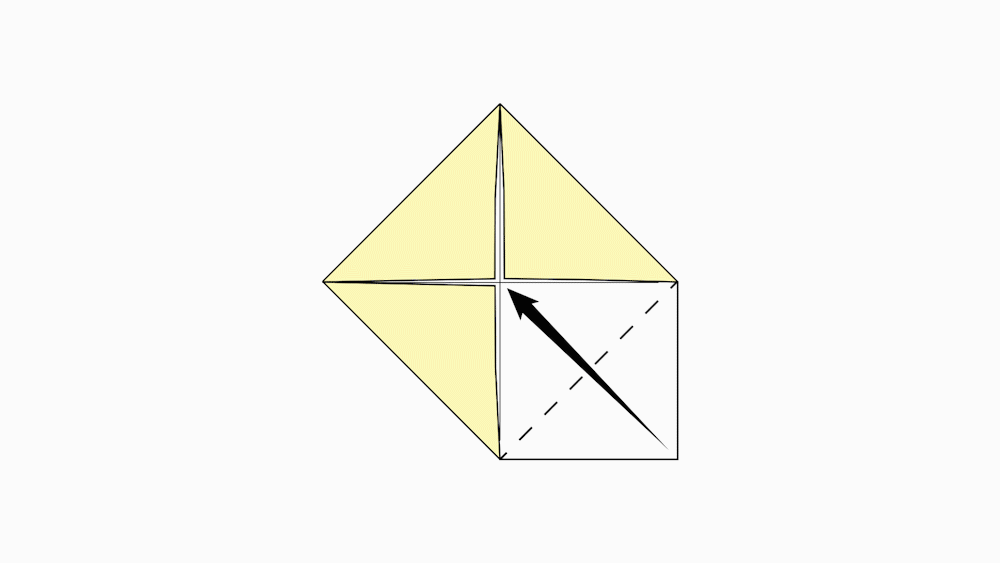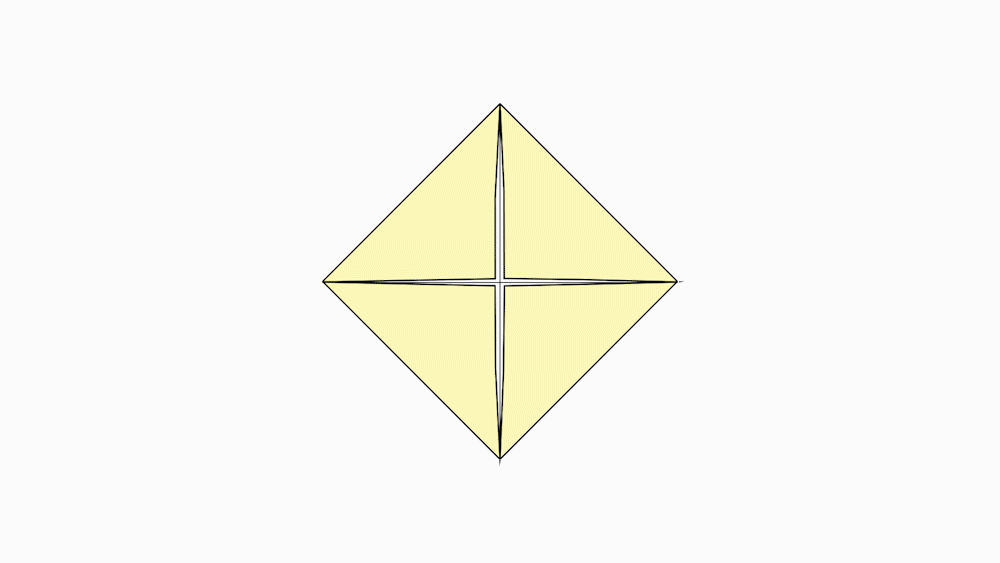
- הוראת קיפול: לקפל כל קדקוד לנקודת מפגש האלכסונים. (לקפל את הקיפול בכל הניירות).
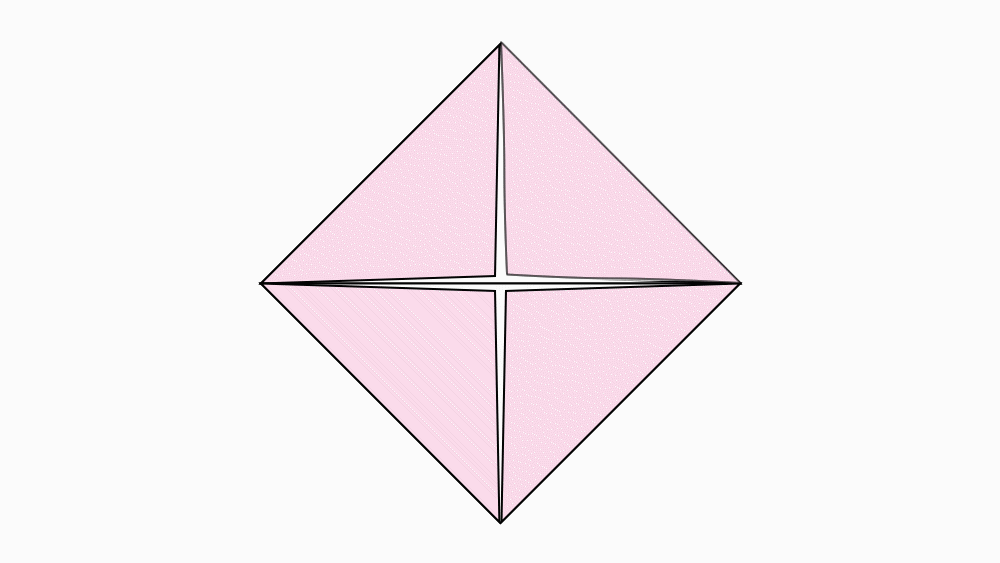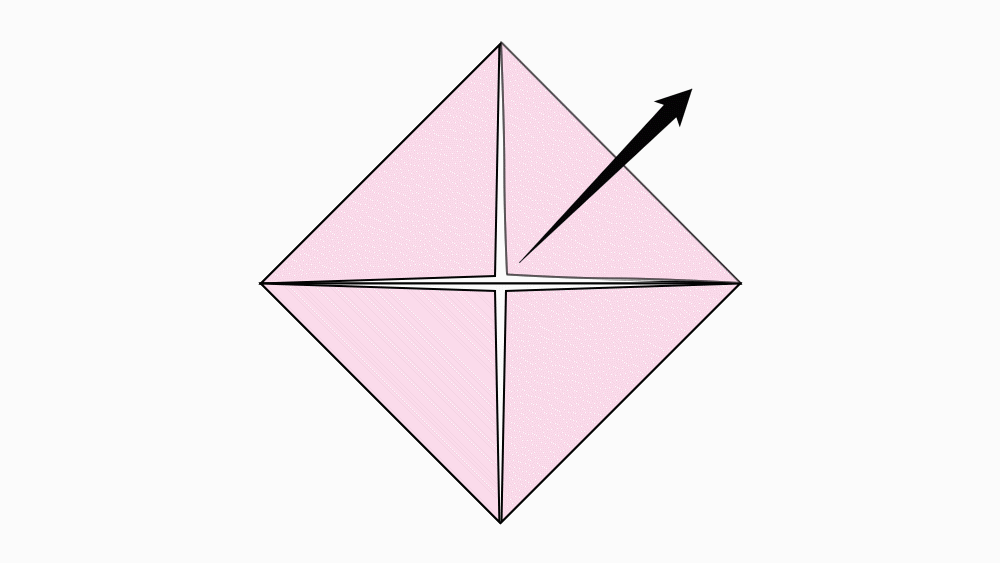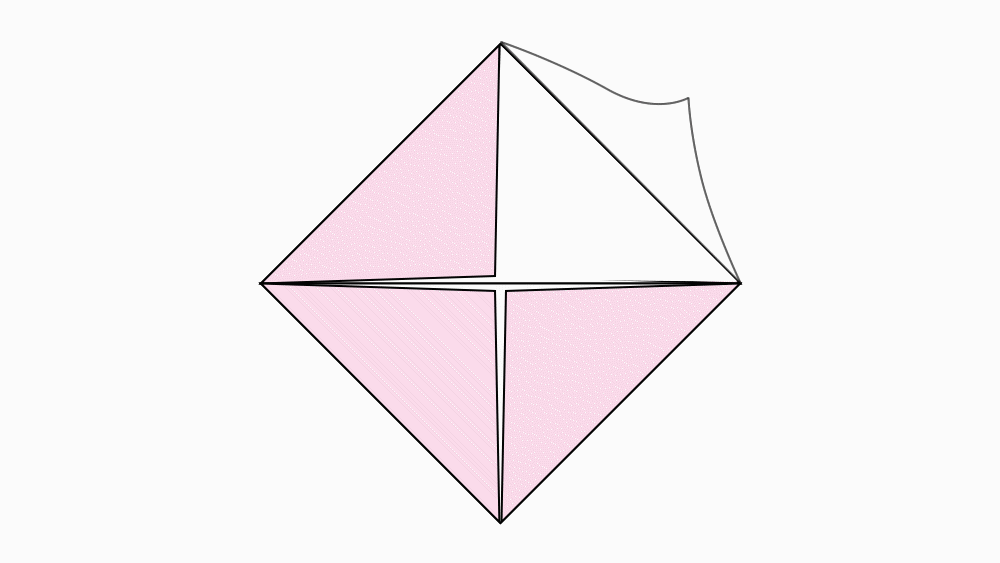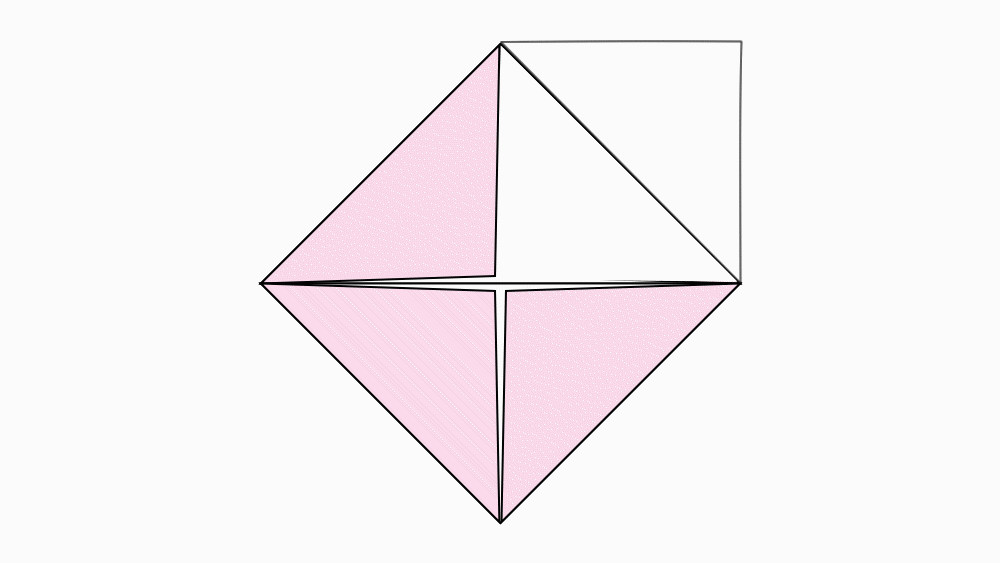
- שאלה לדיון: פיתחו את המשולשים בנייר אחד בלבד, ובחנו, מהו היחס בין השטח של הריבוע הפנימי בצבע לבן הצבעונים.
- המשולשים הם חצי משטח הריבוע
- תשובה: מצאנו כי מידת השטח של המשולשים הצהובים שווים למידת השטח של הריבוע הפנימי. שטחם של ארבעת המשולשים הצהובים וגם של הריבוע הפנימי הוא חצי משטחו של הריבוע לפני שקיפלנו.
- הריבוע הפנימי הוא חצי משטחו של הריבוע לפני שקיפלנו.
- הוראת קיפול: לפתוח משולש אחד, כפי שמודגם באנימציה. (בכל 9 הניירות שקיפלנו)
- הוראת קיפול: לקפל כפי שמודגם באנימציה (בכל הניירות שקיפלנו)
- הוראת קיפול: לקפל את המשולש הלבן בנייר אחד בלבד. כפי שמודגם באיור.
- הוראת קיפול: לקפל קדקוד לקדקוד כפי שמודגם באנימציה. (לקפל ב- 9 דפים).
- הוראת קיפול: להכניס לכיס משולש אחד בלבד כפי שמודגם באנימציה (ב-9 ניירות).
- קיבלנו 8 משולשים ישרי זווית קטנים ומשולש אחד גדול. במשולש ישר-זווית, שתי הצלעות היוצרות זווית ישרה נקראות ניצבים והצלע שמול הזווית הישרה נקראת יתר.
- משימה: בידקו עם המשולשים שקיפלתם, ונייר נוסף בצורת ריבוע. האם ניתן להוכיח כי סכום השטח של הריבועים הנבנים על שני הניצבים שווים לשטח של הריבוע הנבנה על היתר?
- יש 9 משולשים קטנים שהם שמינית מהריבוע הגדול ומשולש אחד שהוא רבע של הריבוע הגדול.
- משימה: האם הוכחתם את משפט פיתגורס עם המשולש הסגול שבתמונה או עם המשולש השחור שבתמונה? הסבירו
- בדגם זה הוכחת משפט פיתגורס משתמשים במשולש שהוא רבע של הריבוע הגדול ועל הניצבים נמצאים 8 משולשים ששטחם ביחד הוא ריבוע שלם.
- משפט פיתגורס: סכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר.
- כל המשולשים במבנה זה הם משולשים קטנים ושטחם הוא שמינית של הריבוע הגדול.
- הוראת קיפול: בנייר נוסף לקפל צלע לצלע מקבילה ולפתוח כפי שמודגם באנימציה.
- הוראת קיפול: לקפל צלע לצלע מקבילה ולפתוח כפי שמודגם באנימציה.
- הוראת קיפול: לקפל כל צלע לצלע לקן הסימטריה ולפתוח כפי שמודגם באנימציה.
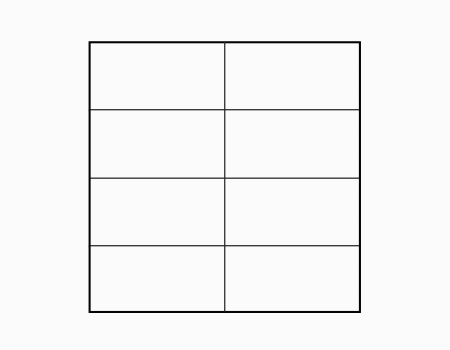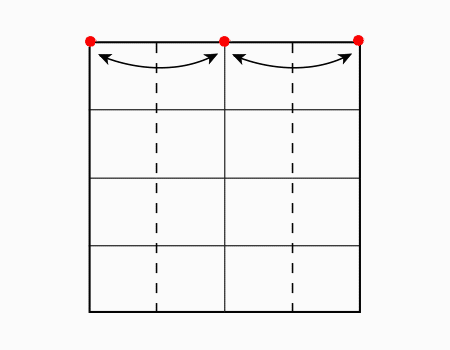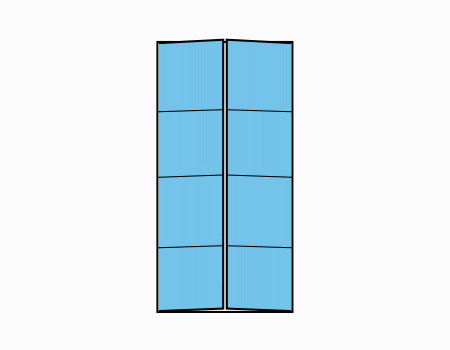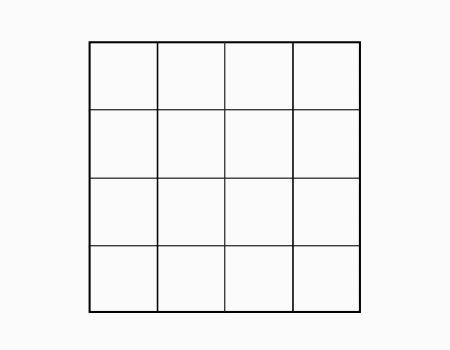
- הוראת קיפול: לסובב את הנייר כפי שמודגם באנימציה.
- הוראת קיפול: לקפל כל צלע לצלע לקו הסימטריה ולפתוח כפי שמודגם באנימציה.
- קיבלנו 16 יחידות שטח של הריבוע הגדול..
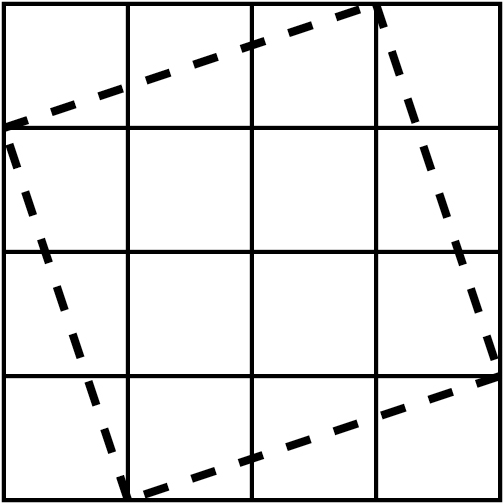
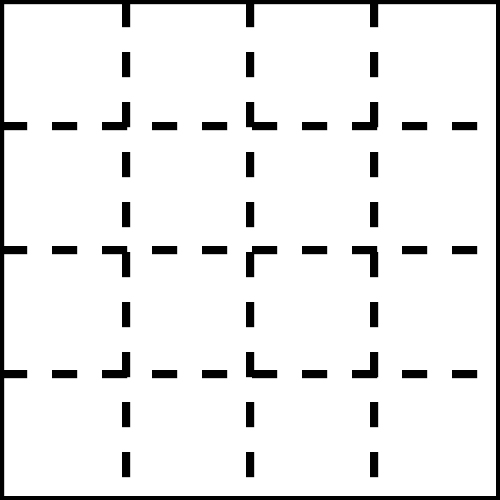
- הוראת קיפול: לשרטט את הישרים המודגמים באיור.
- חשוב שיקחו את הזמן וישרטטו כמו באיור כך שבהמשך יוכלו לתרגל
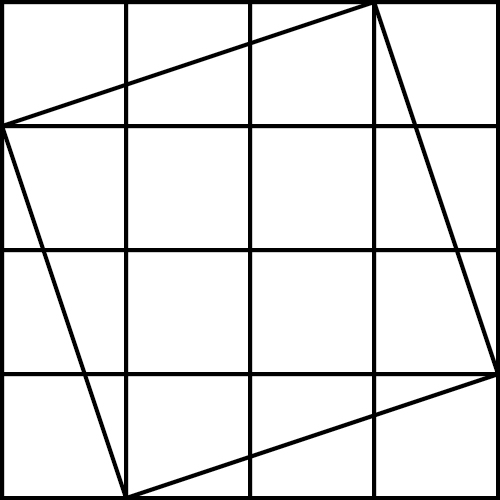
- הוראת קיפול: כך נראה השרטוט , אנא הקפידו על דיוק בשרטוט.
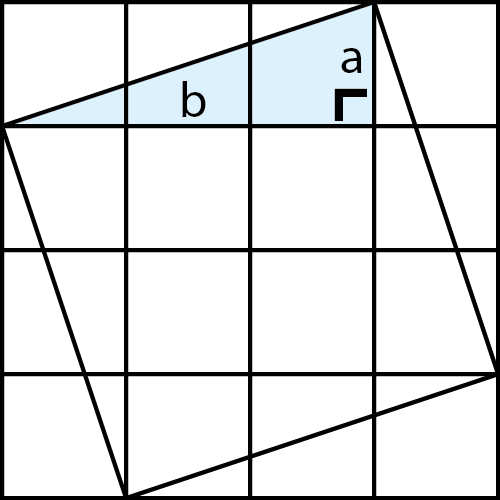
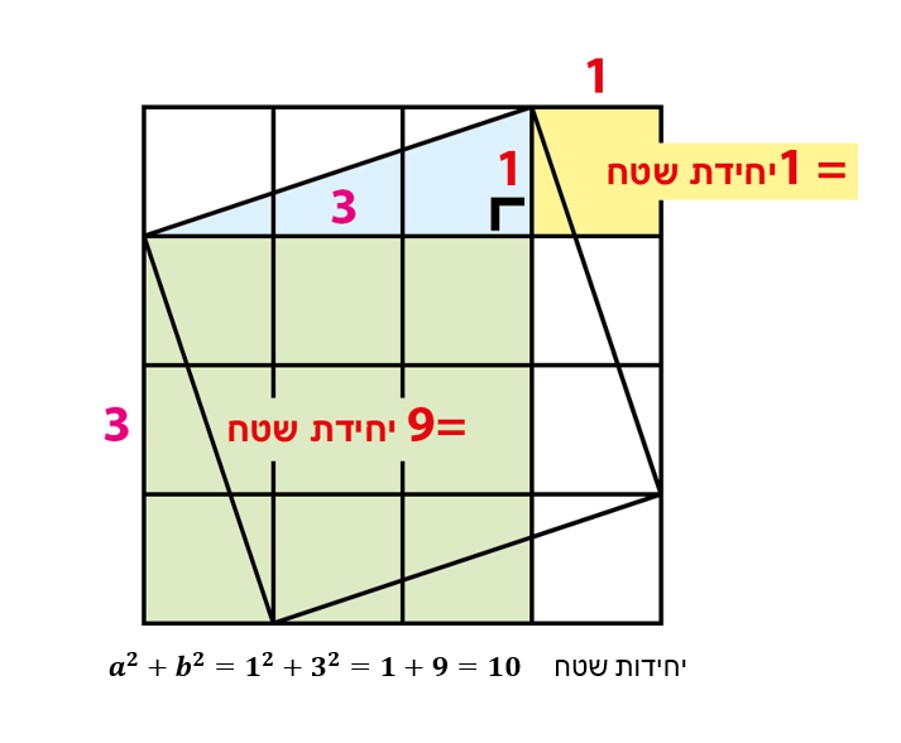
- שאלה לדיון: מהם שטחי הריבועים הנמצאים בצלעות a ו-b?
- ניתן לבקש מהם שיצבעו את כמו באיור.
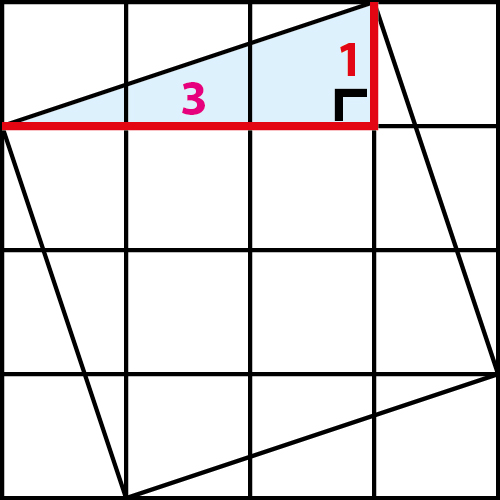
- תשובה1: על הצלע a שטח הריבוע הוא 1 יחידת שטח, ועל צלע b שטח הריבוע הוא 9 יחידות שטח.
- תשובה2: סה”כ סכום השטחים על שני הניצבים הוא 10 יחידות שטח.
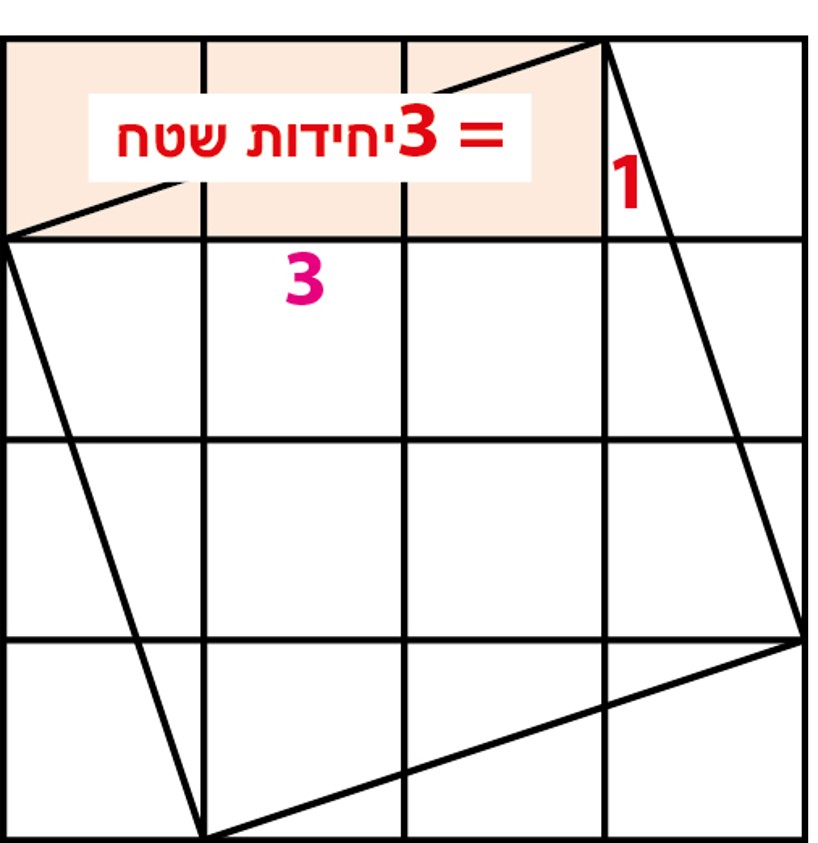
- שאלה לדיון:איך נחשב את מספר יחידות השטח של הריבוע על היתר?הסבירו
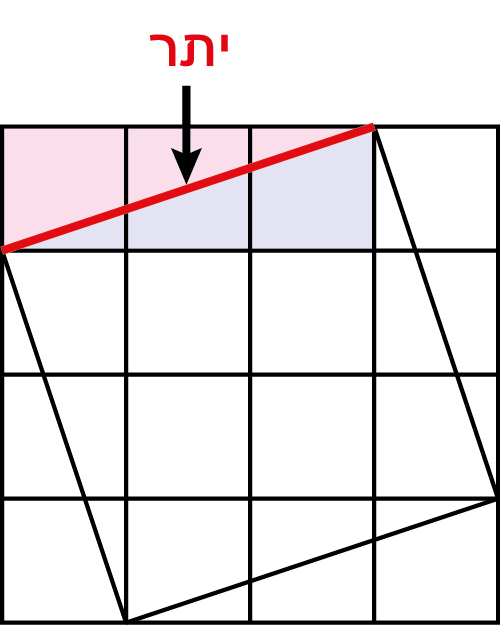
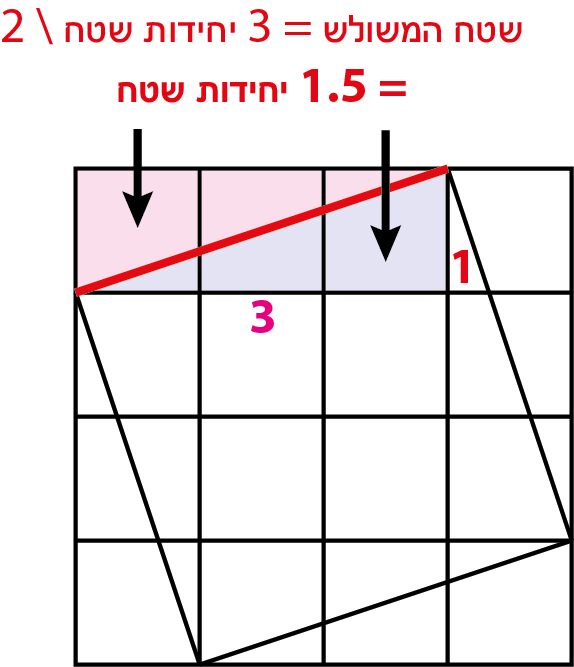
- שאלה לדיון: מהו שטח הריבוע שצלעו הוא היתר של המשולש שאורכי הניצבים הם 1,3 יחידות אורך? מהו שטח המשולש עם ניצבים 1,3 יחידות אורך?
- תשובה: שטח המשולש 1.5 יחדות שטח. שאלת שטח הריבוע על היתר בהמשך הקיפולים.
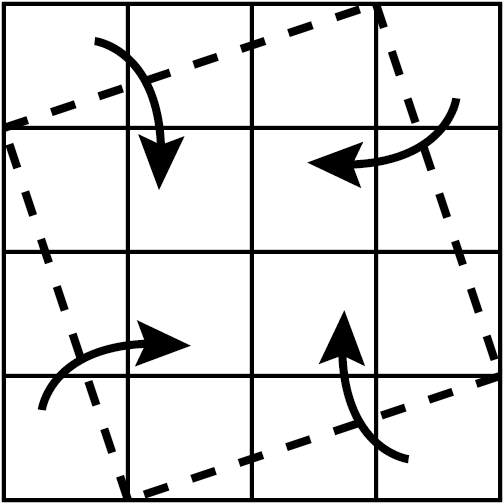
- הוראת קיפול: לקפל כפי שמודגם באיור.
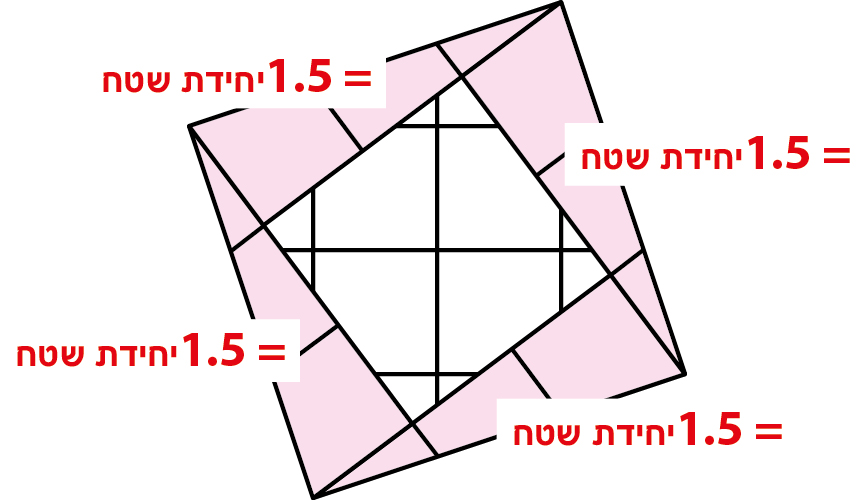
- השטח של המשולשים הצבעונים:1.5+1.5+1.5+1.5 = 6 יחידת שטח.
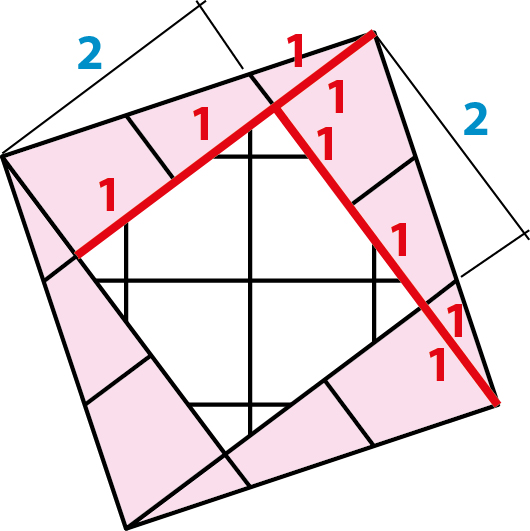
- 2X2=(1+1) X (1+1) =4
  
  4 יחידות שטח
  
  המשולשים הצבעונים+ הריבוע הלבן = 6 יחידות שטח+ 4 יחידות שטח = סה”כ 10 יחידות שטח.
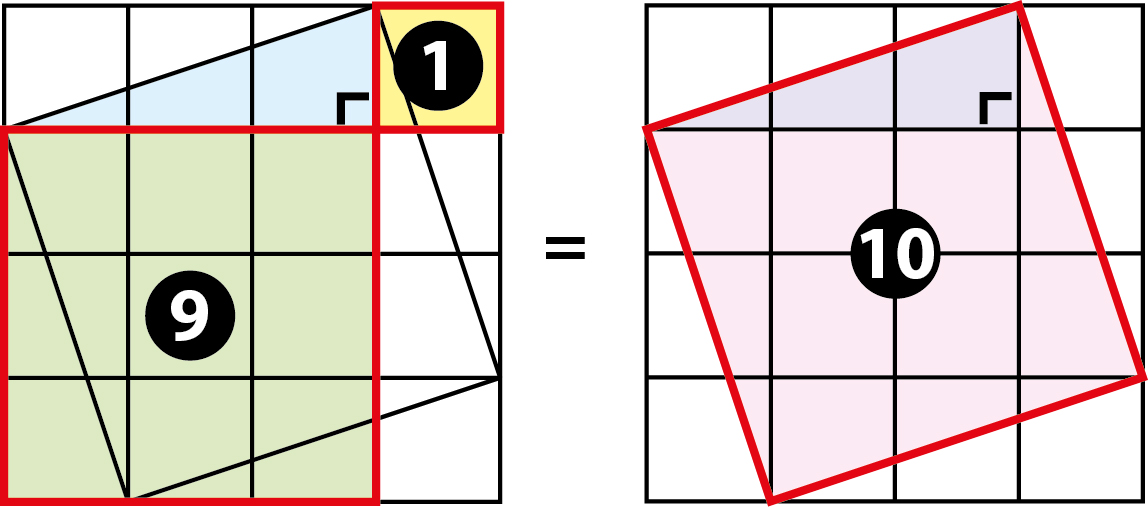
- 9 יחידות שטח +יחידת שטח אחת = 10 יחידות שטח. לכן
  
  $\dpi{300} \bg_black \LARGE a^{2}+b^{2}=c^{2}$
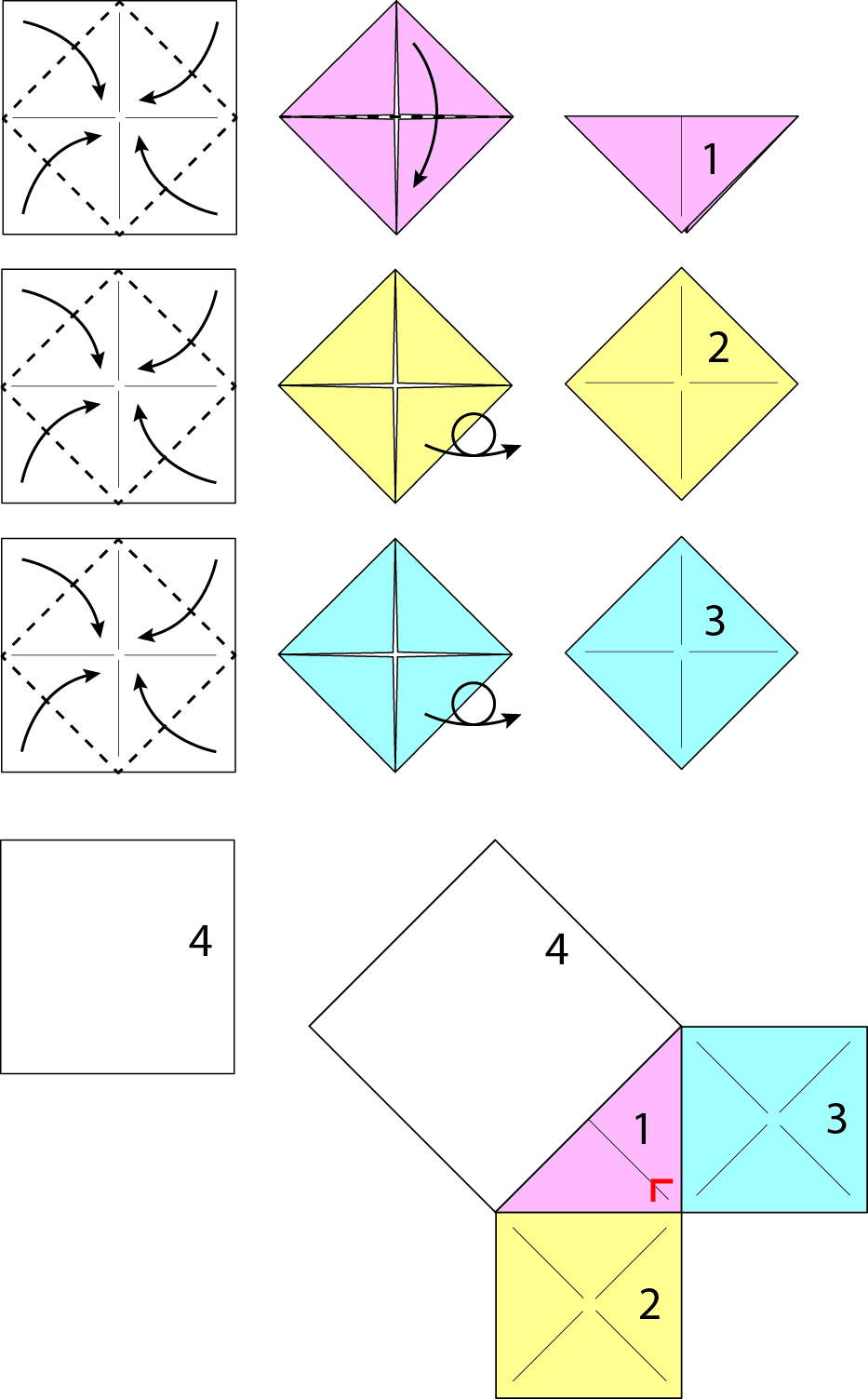
- שאלה לדיון: באיזה אופן אפשר להוכיח כי השטח של הריבועים המסומנים בספרות 3, 2 שווים לשטח של הריבוע המסומן בספרה 4.
- משימה: צרו משולש כפי שמופיע באיור, כך שאורכי הצלעות של המשולש הם:5+3+4.האם תוכלו ליצור משולשים נוספים עם הניירות שיש לכם?
- ניתן ליצור עם הניירות שלושה משולשים: 5+3+4, 6+8+10, 10+6+8
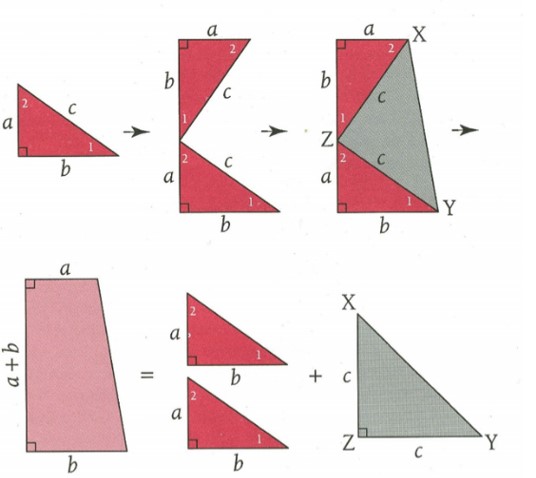
- משימה: כתבו משוואה המקשרת את אורכי הניצבים במשולש הלבן והיתר של המשולש הלבן.
- הוכחה ראשונה של BHASKARA מהמאה 12 הודו
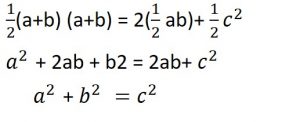
- James Garfield
  נשיא 20 ארה”ב
  1831-1881
- הוכחה: James Garfield
  נשיא 20 ארה”ב
  1831-1881.
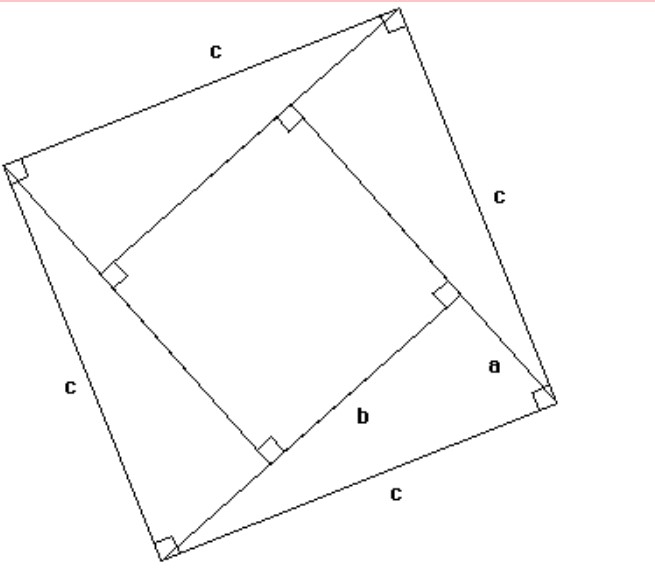
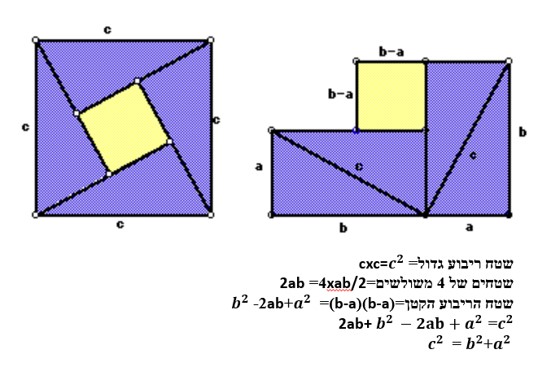
- שטח ריבוע גדול= cxc=c^2
  
  שטחים של 4 משולשים=xab/24= 2ab
  
  שטח הריבוע הקטן=(b-a)(b-a)=a^(2 )+ab2- b^2
  
  c^2=2ab+ b^(2 )-2ab+a^(2 )
  
  a^(2 )+b^2 = c^
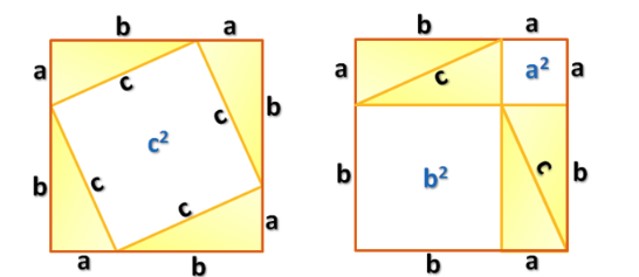
- הוכחה אלגבראית של שילוב גיאומטרי ואלגבראי במשפט פיתגורס.
- משולש מצרי על ידי קיפול
  משולש ABF יחס 3:4:5
- משימת סיכום : לקפל את הנייר בדרכים שונות על מנת להוכיח מדוע הקיפול נותן חצי משטח הריבוע הנתון.
- .
- כל אחד מהמשולשים שקיפלתם, יכול לשמש כסימניה לספר.

מטרות הפעילות
- התלמידים יתנסו ויכירו את היחס של הנייר המקופל לנייר לפני הקיפול.התלמידים יכירו והתנסו במשפט פיתגורס על ידי פירוק והרכבה.

שם הדגם
סימניות לספרים.

על השיעור
התלמידים יכירו והתנסו בפירוק והרכבה במשפט פיתגורס ויכירו הוכחות גיאומטריות והוכחות אלגבראיות עם קיפולי נייר

ידע נדרש
משולש ישר זווית, גובה במשולשים ויחס של שטחים.

ציוני דרך
משולש ישר זווית: מושגים: ניצב, יתר
משפטים נלווים:
– משפט פיתגורס: במשולש ישר זווית סכום ריבועי הניצבים שווה לריבוע היתר.
– שני משולשים ישרי זווית שלהם ניצב שווה ויתר שווה חופפים זה לזה.
קישור לתכנית הלימודים

מילון מונחים בגאומטריה

חומרים
שישה דפי אוריגאמי צבעונים וארבעה ניירות משובצים לכל תלמיד.

גאומטריה לחטיבת ביניים|

משוב מעמיתים

שדה חובה*

You must be logged in to post a comment.