Sorry, you have Javascript Disabled! To see this page as it is meant to appear, please enable your Javascript! See instructions here

שברים יסודיים 1/3

שברים יסודיים 1/3

שברים יסודיים 1/3

- כל תלמיד יבחר שני דפים גדולים ושלושה דפים קטנים.
- כל תלמיד יקבל שני ניירות גדולים (15ס”מ/ 15ס”מ) ושלושה ניירות קטנים. (10ס”מ/ 10ס”מ).
- הניחו לפניכם: שני דפים גדולים ושלושה דפים קטנים.
- הוראת קיפול: לקפל ב- 5 ניירות צלע לצלע מקבילה ולפתוח.
- נקפל בכל הניירות.
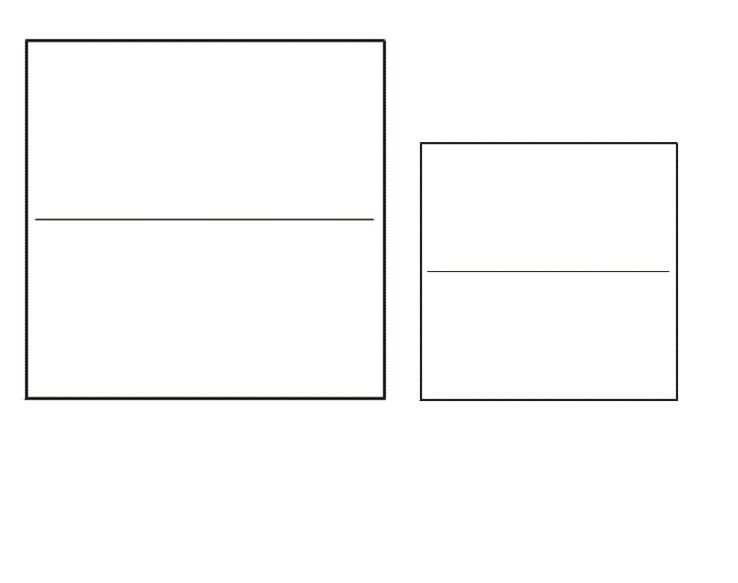
- משימה: הניחו על השולחן ריבוע אחד גדול וריבוע אחד קטן כמו באיור.
- שאלה לדיון: האם נוכל לומר שגודל שטחו של כל מלבן שהתקבל לאחר הקיפול הוא חצי משטחו של הריבוע שממנו מורכבים שני המלבנים? האם זה יתכן גם בדף הגדול וגם בדף הקטן? הסבירו
- תשובה: גם בנייר הגדול וגם בנייר הקטן, המלבן הוא חציו של השלם. (השלם הוא הנייר בצורת ריבוע).
- כשאומרים חצי הכוונה לחצי ביחס לשלם נתון. כי יתכן שחצי אחד אינו שווה לחצי אחר במקרה שלנו כאשר מציגים שני דפים (שלמים) בגדלים שונים.
- הוראת קיפול: להמשיך ולקפל במלבן הגדול והקטן צלע קצרה לצלע מקבילה.
- הוראת קיפול: לפתוח בחזרה לריבוע בשני הדפים שקיפלנו.
- שאלה לדיון: סמנו עם המודד את קווי הקיפול שהתקבלו לאחר הקיפול. מהו גודל השטח של כל אחד מהריבועים שנוצרו? כמה ריבועים קטנים יש בנייר לאחר הקיפול? הסבירו
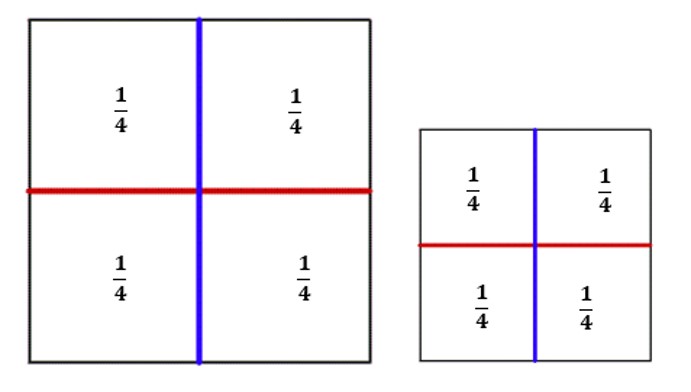
- במקרה הזה כל הריבועים הקטנים חופפים. גודל שטחו של כל ריבוע קטן הוא רבע משטחו של הריבוע הגדול. בהמשך נראה מצבים בהם הרבעים המסומנים אינם חופפים אך גודל שטחם הוא שווה.
- תשובה: בכל ריבוע שטחו של הריבוע האדום הוא רבע מגודלו של הריבוע השלם. לאחר הקיפול נוצרו 4 ריבועים שווה שטח בכל ריבוע שלם.
- תשובה: נוכל לסמן כל רבע עם השבר היסודי $\dpi{150} \bg_white \large \frac{1}{4}{\color{DarkBlue} }$ . בכל אחד מהריבועים השלמים יש 4 ריבועים השווים בשטחם.
- יש צורך לקשר בין היצוג המילולי (לדוגמא: רבע), הסמל $\dpi{120} \large \frac{1}{4}$ והיצוג הויזואלי (המלבן). יש להמשיך בכל השיעורים להדגיש את הקישור בין המספר למילולי והיצוג הויזואלי).
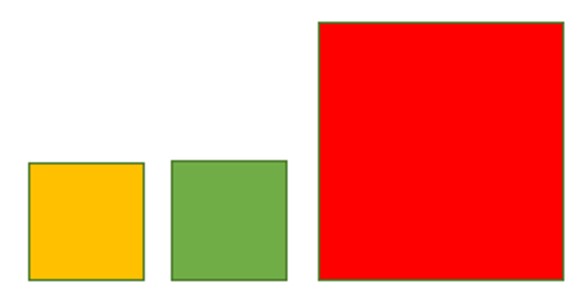
- הניחו לפניכם: 2 ניירות קטנים ונייר 1 גדול.
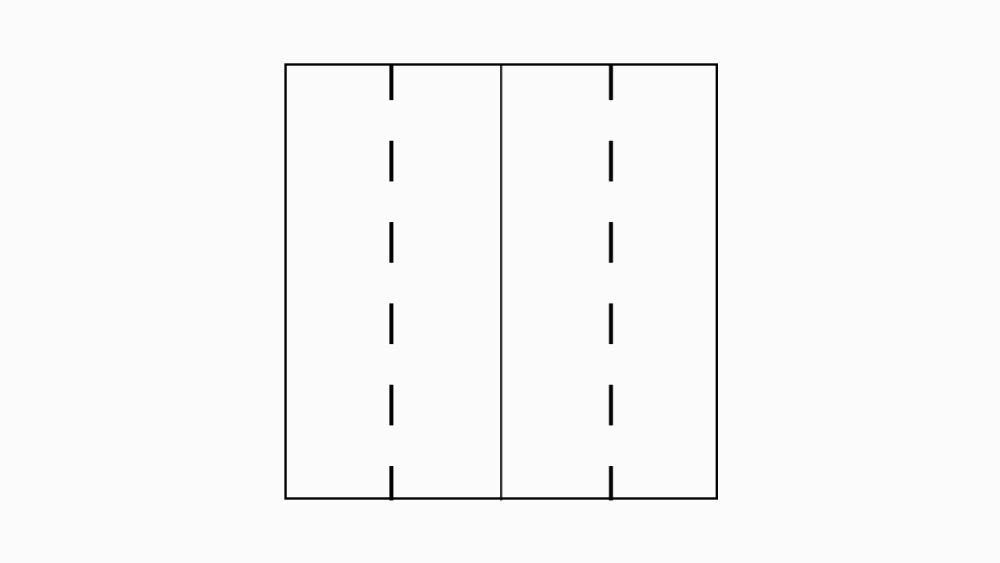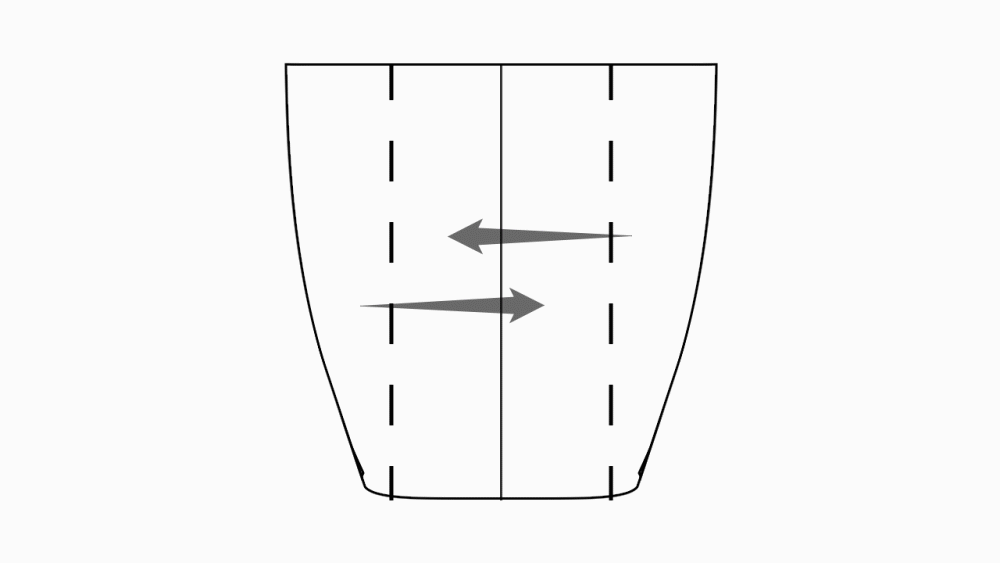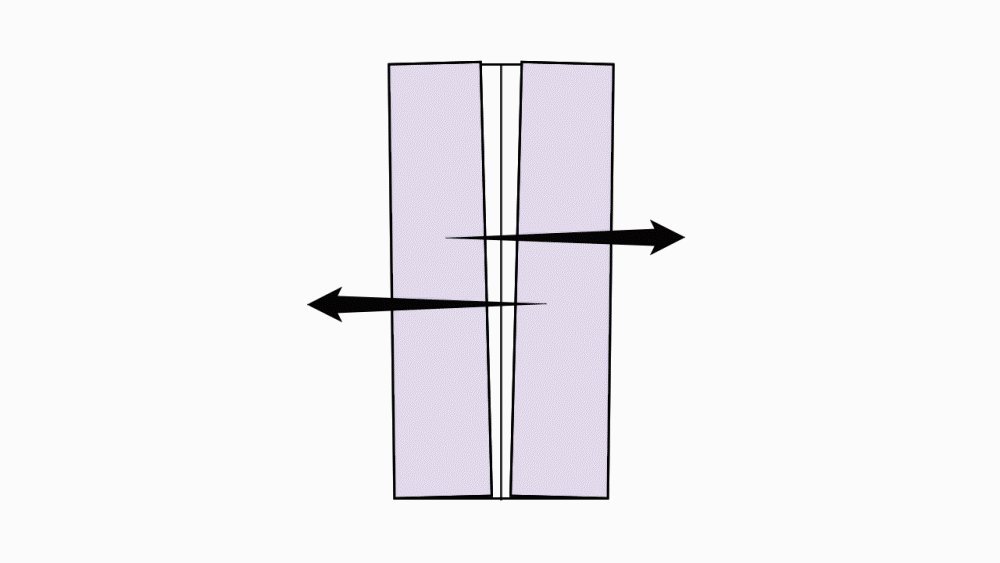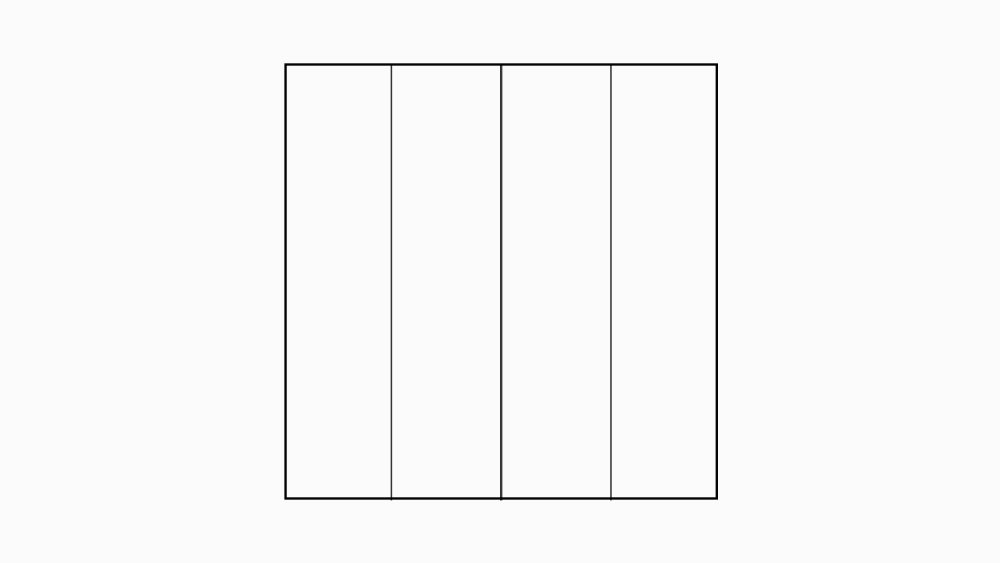
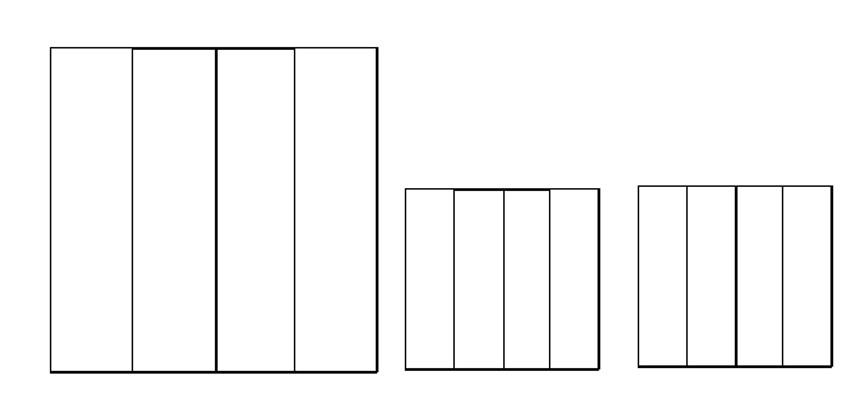
- הוראת קיפול: ב- 2 ניירות קטנים נוספים ובנייר 1 גדול לקפל כל צלע לקו הסימטריה ולפתוח כפי שמודגם באנימציה.
- משימה: סמנו עם המודד את קווי הקיפול בכל אחד מהניירות שקיפלתם.
- שאלה לדיון: מהו גודל השטח של כל אחד מהמלבנים שנוצרו לאחר ששרטטתם את קווי הקיפול? כמה מלבנים שווים בגודלם יש בכל אחד מהריבועים שקיפלתם? הסבירו
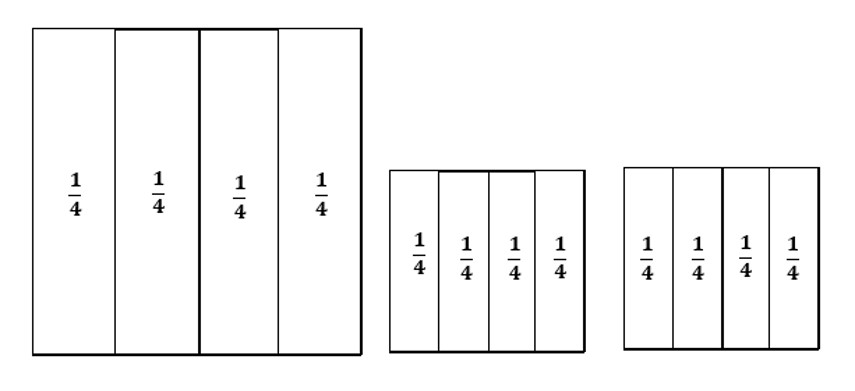
- במקרה הזה כל המלבנים בכל ריבוע שלם חופפים. גודל שטחו של כל מלבן קטן הוא רבע משטחו של הריבוע השלם. בהמשך נראה מצבים בהם הרבעים המסומנים אינם חופפים אך גודל שטחם הוא שווה.
- תשובה 1: גודל השטח של כל אחד מהמלבנים הוא רבע מהריבוע השלם. נסמן כל מלבן בשבר היסודי $\dpi{150} \bg_white \bg_white \frac{1}{4}$ .
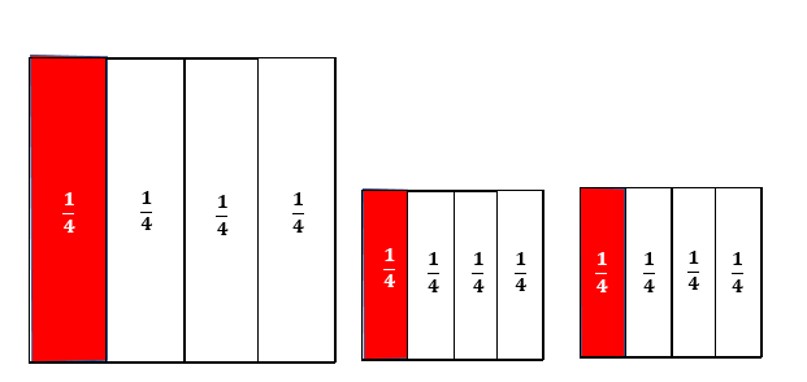
- תשובה 2: יש 4 מלבנים בכל אחד מהריבועים השלמים שגודל שטחם הוא $\dpi{150} \bg_white \bg_white \frac{1}{4}$ משטח הריבוע.
- יש להדגיש שיוויון שטח של כל ארבעת המלבנים.
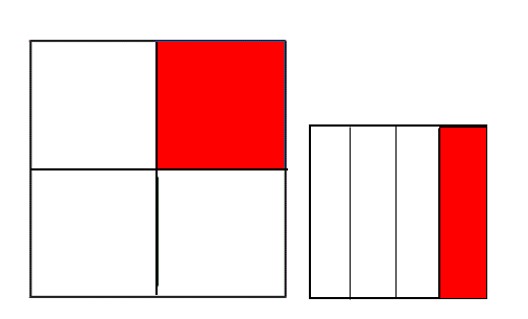
- שאלה לדיון: מהו גודל שטחו של כל אחד משני המצולעים המסומנים באדום? איזה שבר יסודי מציין את גודל שטחו של כל אחד מהמצולעים האדומים? הסבירו.
- כאן המקום לציין שכל מצולע אדום (בפרט שאינם חופפים) מיצג גודל שטח של רבע. אבל הוא רבע ביחס לשלם. במקרה שלפנינו השלמים אינם שווים בגודל שטחם.
- תשובה: גודל שטחו של כל מצולע אדום הוא רבע משטחו של הריבוע השלם. הוא מיוצג על ידי השבר היסודי $\dpi{150} \bg_white \bg_white \frac{1}{4}$ מאחר שיש בכל ריבוע שלם 4 צורות שוות שטח.
- שאלה לדיון: האם שני המרובעים המסומנים באדום שווים בשטחם?הסבירו.
- תשובה: גודל שטחם של שני המרובעים האדומים אינם שווים מאחר שכל רבע הוא ביחס לשלם השונה בגודלו.
- הניחו לפניכם: שני ניירות קטנים ונייר אחד גדול.
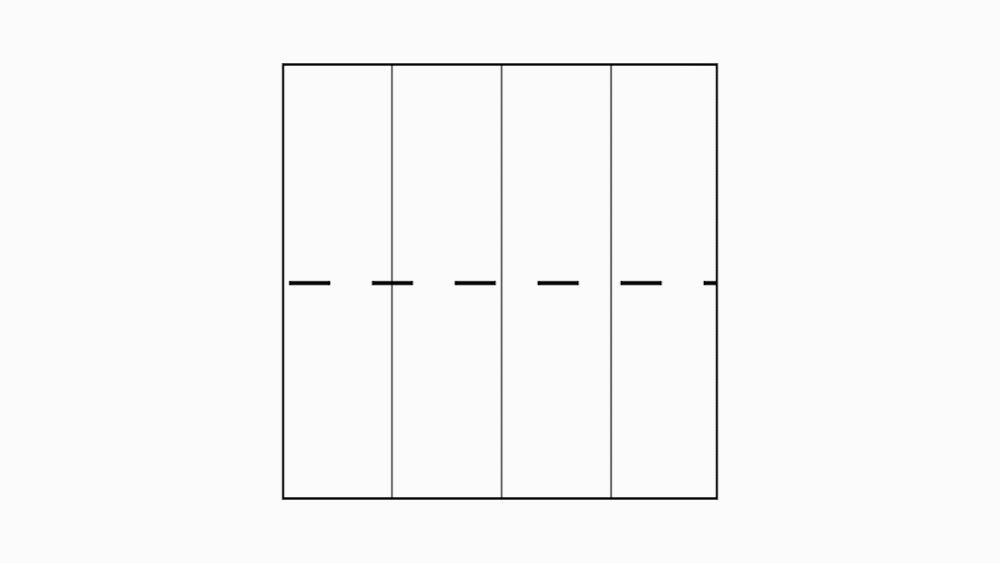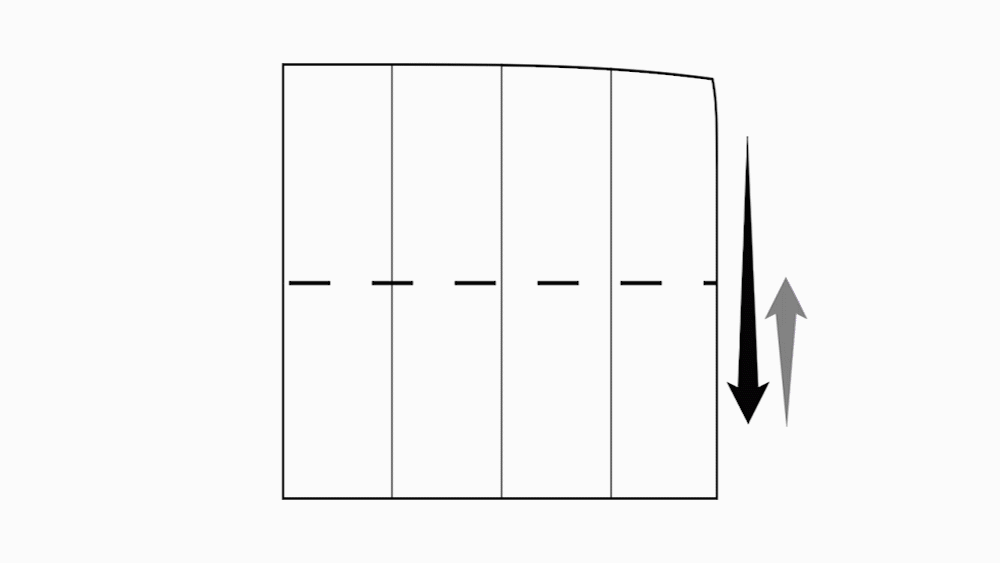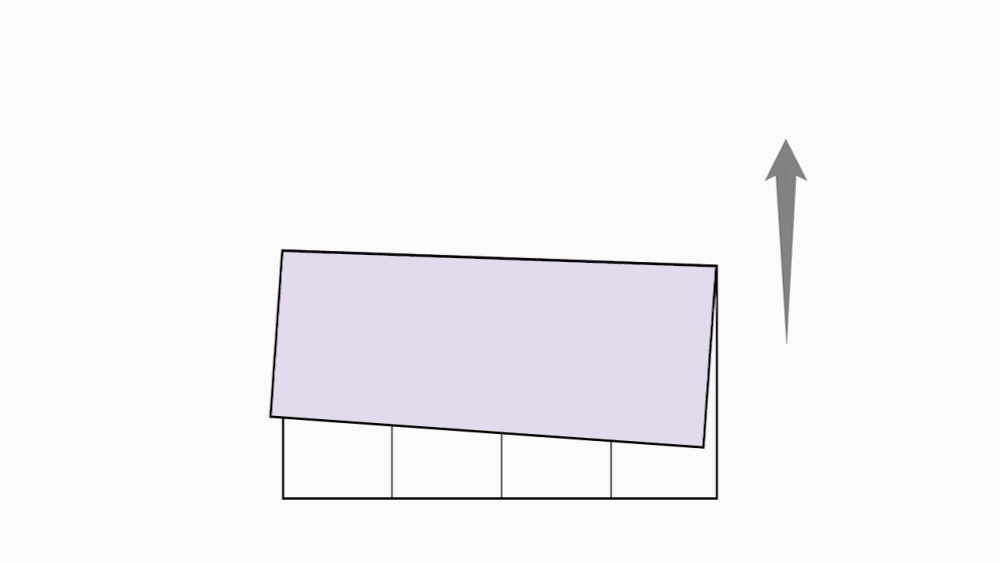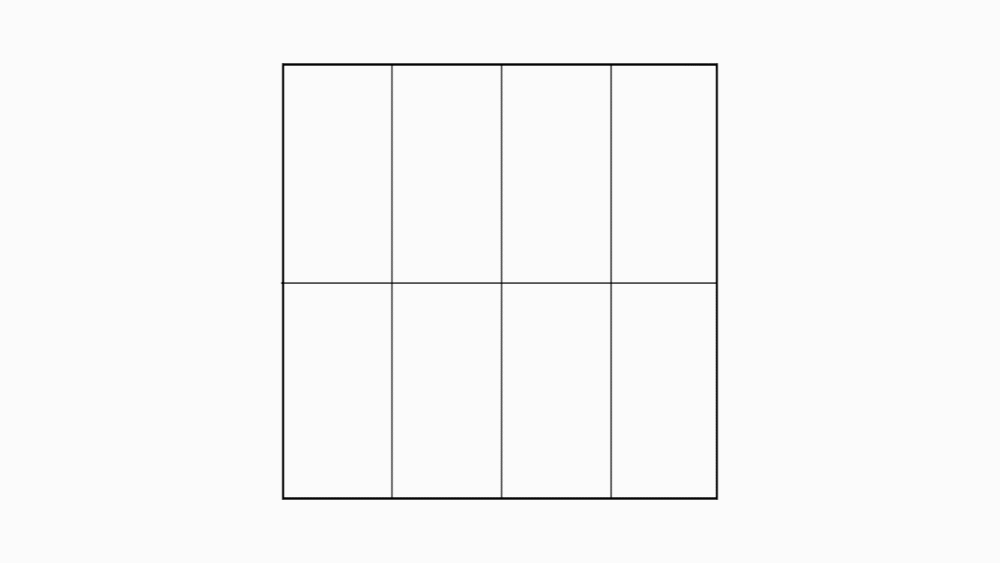
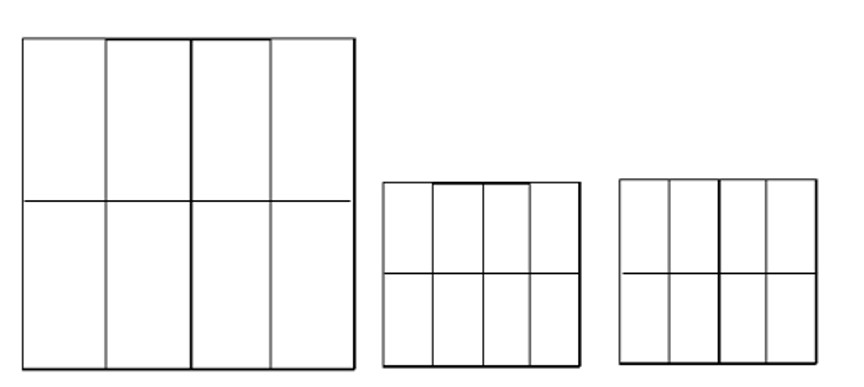
- הוראת קיפול: לקפל בשני הניירות הקטנים ובנייר אחד גדול צלע לצלע מקבילה ולפתוח כפי שמודגם באנימציה.
- לשים לב שהתלמידים ממשיכים לקפל בדפים הנכונים. מומלץ לעבור בין התלמידים ולראות שהם יקפלו בדפים המתאימים.
- משימה : סמנו בכל אחד מהניירות את קו הקיפול החדש שהתקבל.
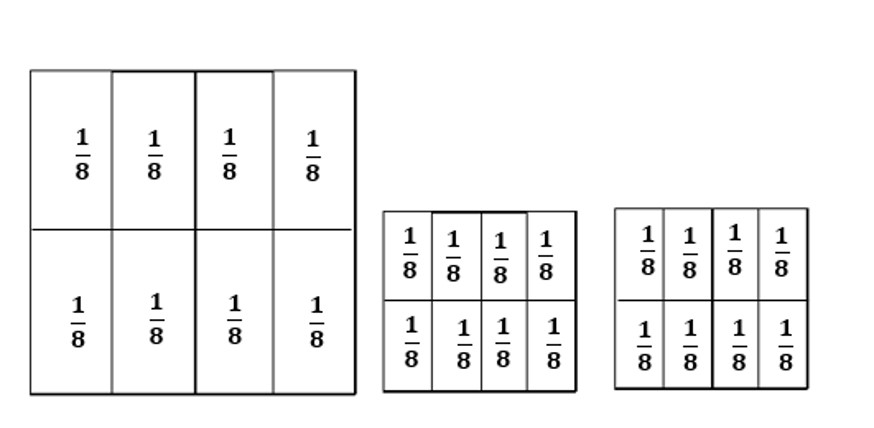
- שאלה לדיון: מהו גודל השטח של כל אחד מהמלבנים שנוצרו לאחר ששרטטתם את קווי הקיפול? כמה מלבנים שווה שטח יש בכל אחד מהריבועים שקיפלנו?הסבירו
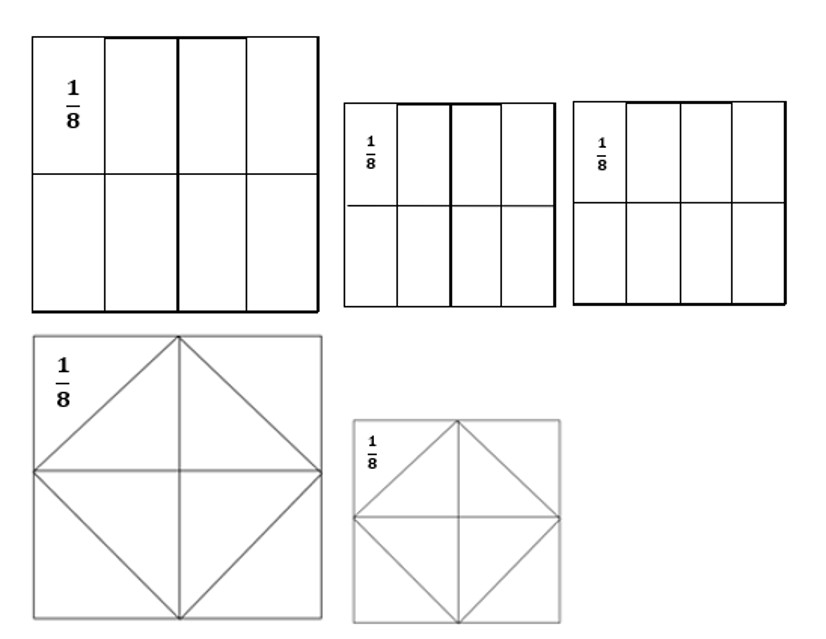
- תשובה 1:בכל ריבוע שלם יש 8 שמיניות שהם שווים בגודל שטחם. נוכל לסמן כל שמינית עם השבר היסודי $\dpi{150} \bg_white \bg_white \frac{1}{8}$ .
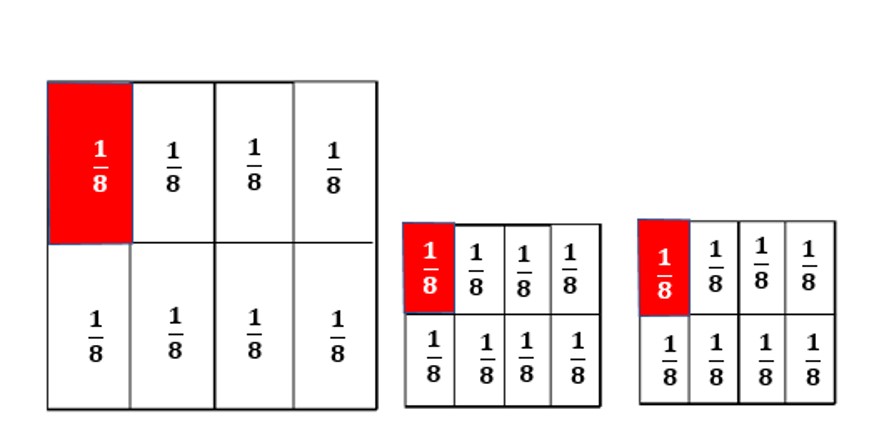
- תשובה 2: בכל ריבוע שלם יש 8 שמיניות, השמינית של כל שלם מסומנת באדום.
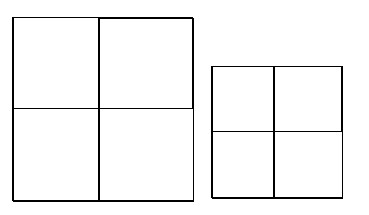
- הניחו לפניכם: נייר 1 גדול ונייר 1 קטן שכבר קיפלנו לרבעים.
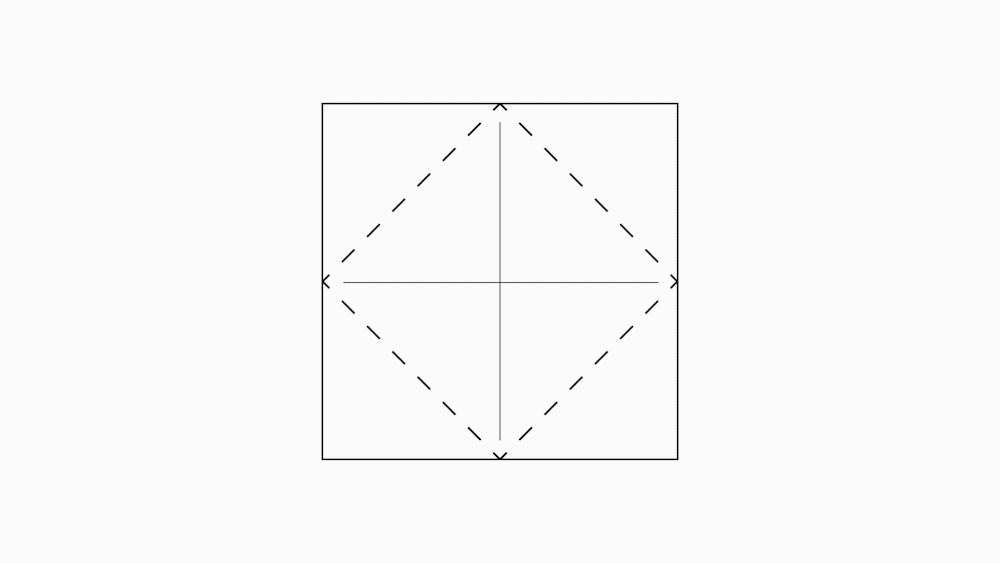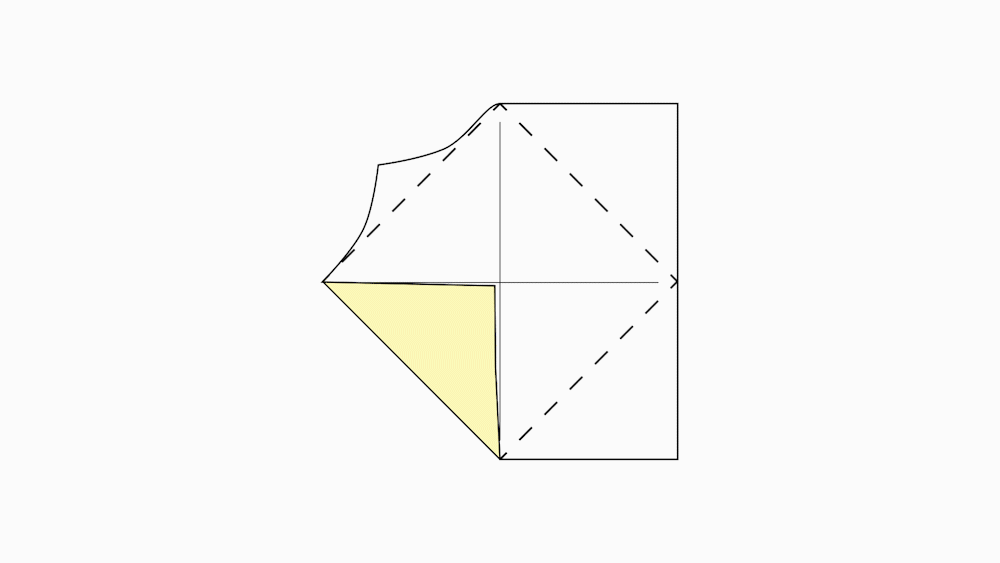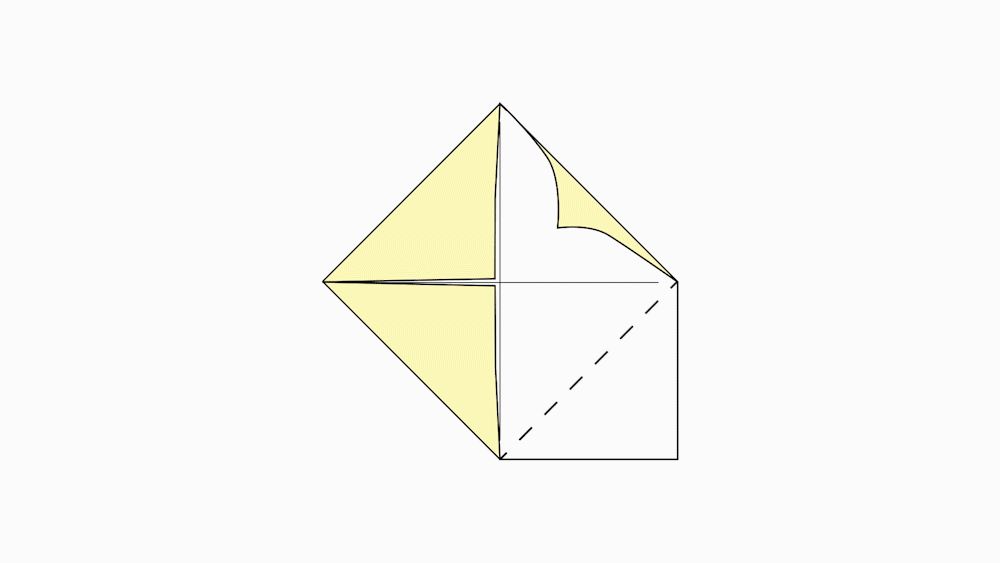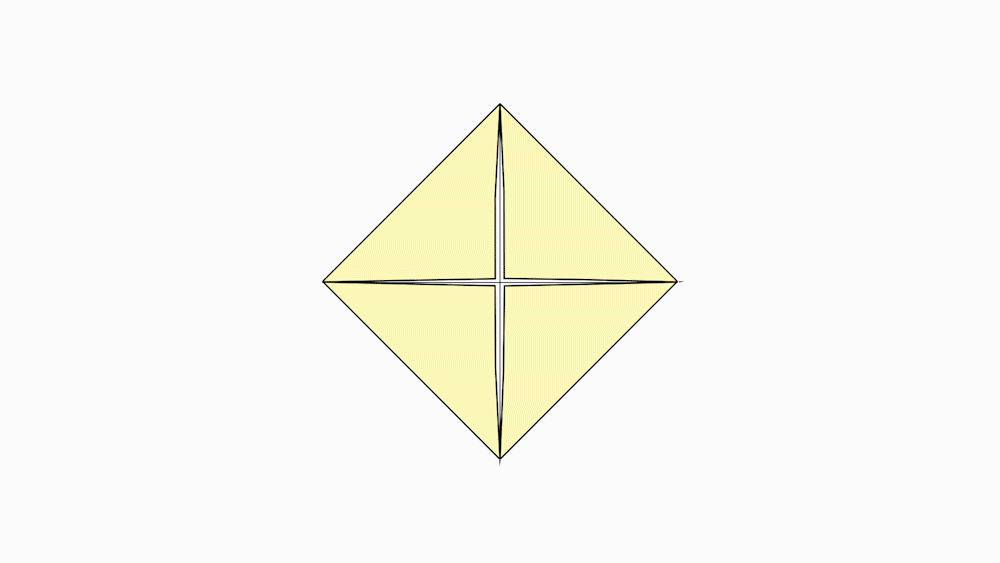
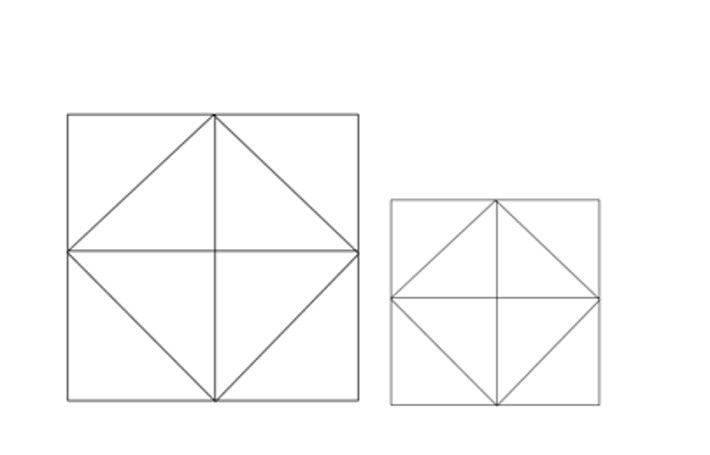
- הוראת קיפול : בשני הניירות (נייר גדול, ונייר קטן). לקפל כל קדקוד לנקודת מפגש קווי הסימטרייה ולפתוח.
- משימה: סמנו עם המודד בכל אחד מהניירות את קווי הקיפול החדש שהתקבלו.
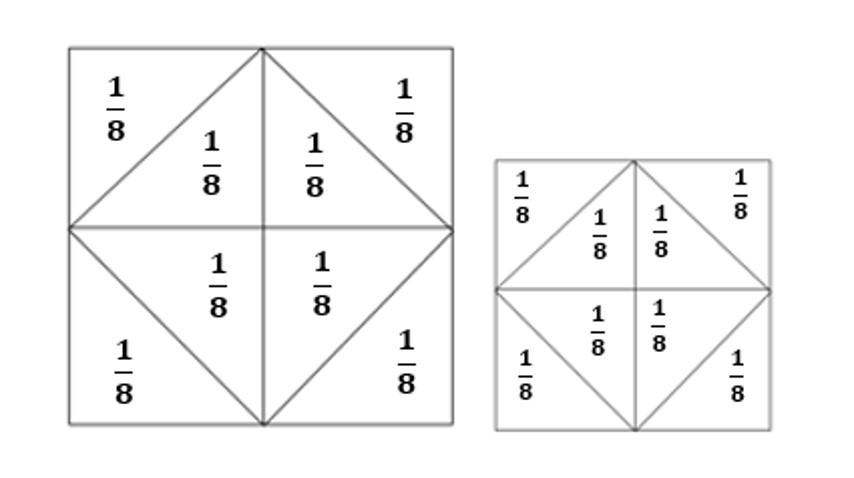
- שאלה לדיון: מהו גודל השטח של כל אחד מהמשולשים לאחר ששרטטתם את קווי הקיפול? כמה משולשים שווה שטח יש בכל ריבוע שקיפלנו?הסבירו
- תשובה1: כל משולש הוא שמינית מהריבוע השלם נסמן אותו בשבר היסודי $\dpi{150} \bg_white \bg_white \frac{1}{8}$ .
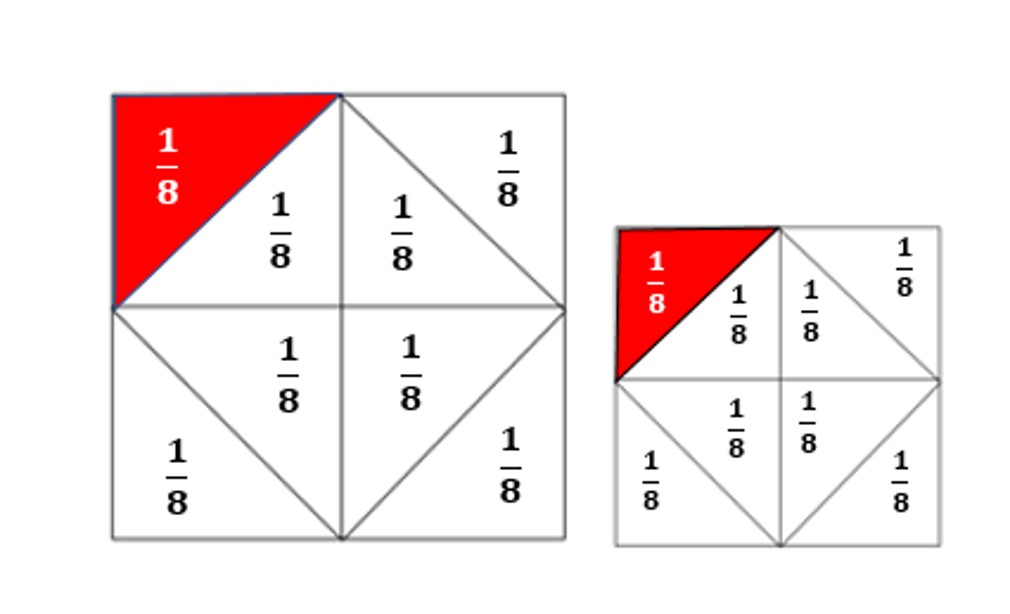
- תשובה 2: בכל ריבוע שלם יש 8 שמיניות שווה שטח המשולש המסומן באדום הוא שמינית.
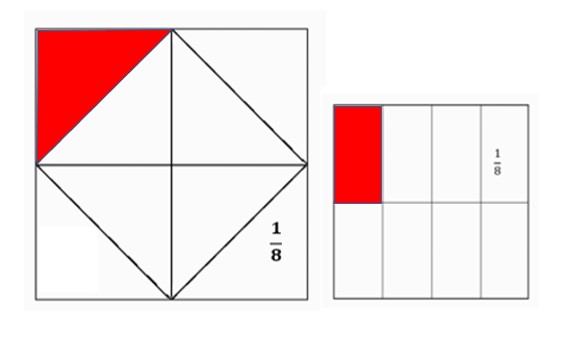
- שאלה לדיון: האם שני המצולעים המסומנים באדום שווים בשטחם? הסבירו.
- תשובה: גודל שטחם של שני המצולעים האדומים אינם שווים מאחר שכל שמינית היא ביחס לשלם השונה בגודלו.
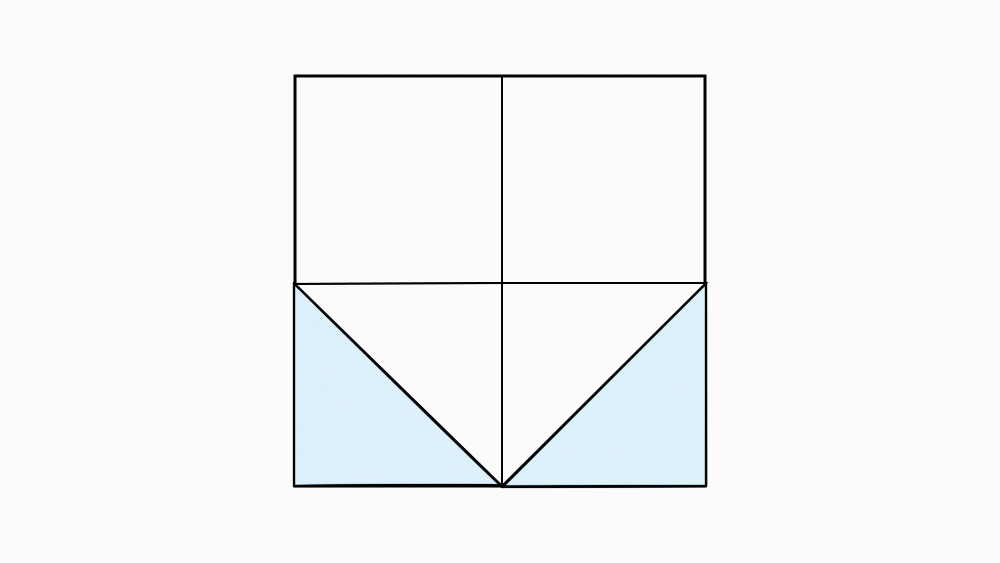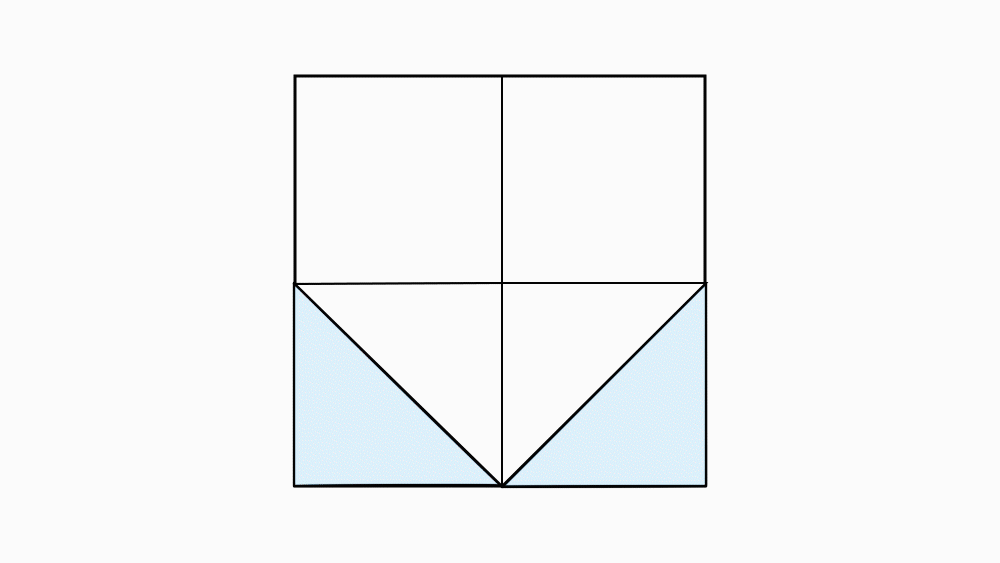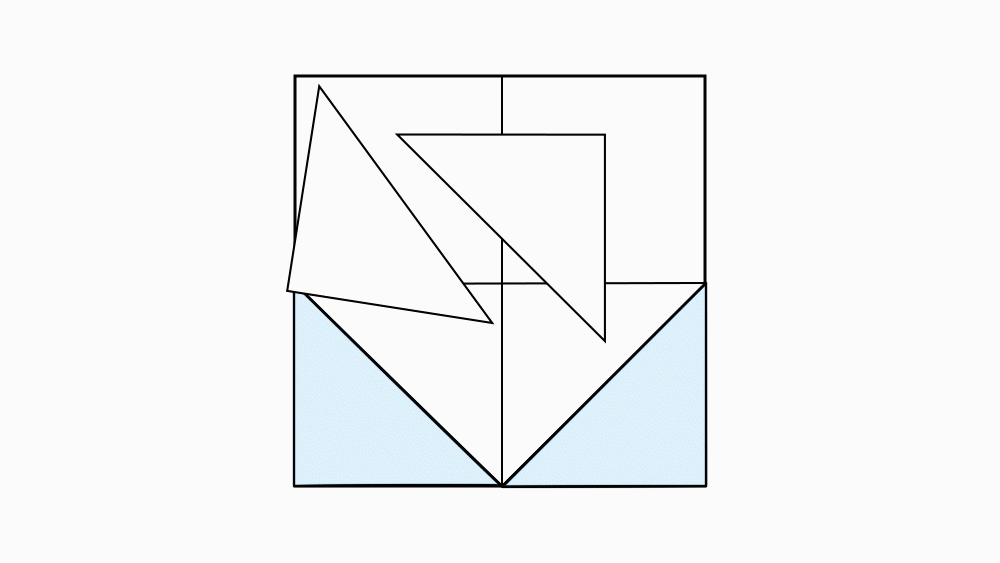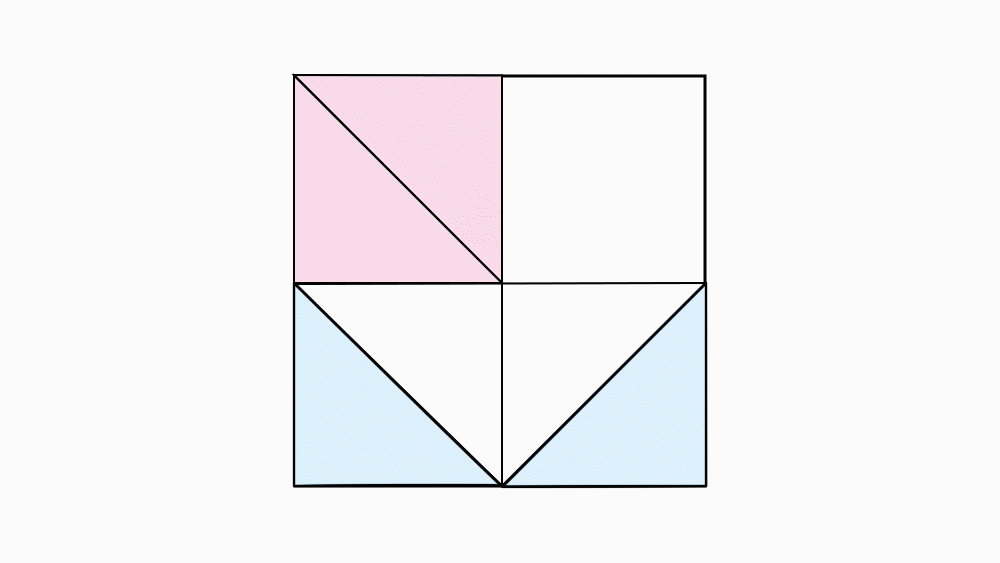
- שאלה לדיון: בחנו איזה חלק מתוך השלם הוא השטח של שני המשולשים הכחולים. ואיזה שטח מתוך השלם ארבעת המשולשים (הכחולים והורודים ביחד)? הסבירו.
- תשובה: השטח של שני המשולשים הורודים הוא $\dpi{150} \bg_white \bg_white \frac{1}{4}$ משטחו של הריבוע. גם שני המשולשים הכחולים הם $\dpi{150} \bg_white \bg_white \frac{1}{4}$ משטחו של הריבוע. וארבעת המשולשים ביחד הם $\dpi{150} \bg_white \bg_white \frac{1}{2}$ משטחו של הריבוע.
- שאלה לדיון: בחנו איזה חלק מתוך השלם הוא השטח של משולש כחול אחד ? ואיזה חלק מהשלם הוא משולש ורוד אחד?הסבירו
- תשובה: משולש ורוד אחד הוא שמינית של הריבוע השלם. משולש כחול אחד הוא שמינית של הריבוע השלם.
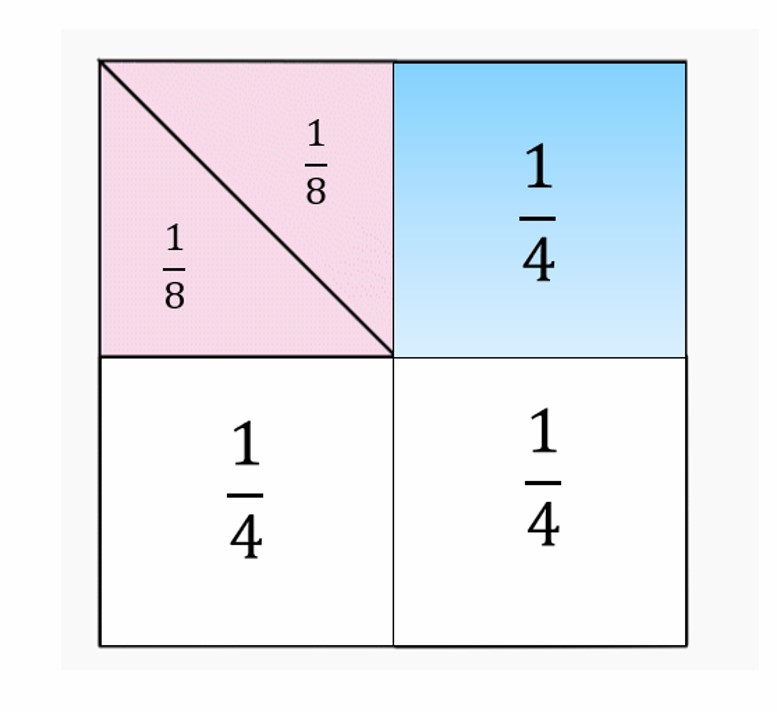
- שאלה לדיון: כמה שמיניות יש בכל רבע של הריבוע השלם? הסבירו
- תשובה: בכל רבע של הריבוע השלם יש שתי שמניות.
- סיום הפעילות: רישמו את שמכם על הניירות שקיבלתם. ושימרו את הדפים לפעילות ההמשך.
- מומלץ לבקש מהתלמידים לכתוב את שמם ולאסוף את הניירות. לשיעור הבא.

מטרת הפעילות
- הכרת השברים היסודיים באמצעות מודל השטח.
- הכרת השבר הפשוט ורישומו כמונה ומכנה.
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.

שם הדגם
ללא דגם

בשיעור זה התלמידים יכינו את הקיפולים. ובשיעור הבא יקפלו מהם הדגם של עץ.

מספר סידורי: 3023

שם היוצר/ת
מירי גולן

© כל הזכויות שמורות למרכז הישראלי לאוריגאמי

רצף מומלץ
מומלץ ללמד לפי הרצף המופיע באתר (בהתאם לתכנית הלימודים).

על השיעור
שיעור 1 מתוך 2

התלמידים יקפלו 5 דפים בגדלים שונים ובכל שלב יחקרו את החלקים מתוך השלם לאחר פעילויות של קיפול כשהשלם הוא בגדלים שונים.

פעילות זו היא תשתית עבור הוראת שברים בהמשך.

ציוני דרך
כיתה ג -עמוד 26

מילון מונחים בגאומטריה

הדגשים בהוראת השבר כחלק משלם:
1. קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
2. החלקים לא חייבים להיות חופפים.
3. כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
4. חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
5. כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
6. השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול יותר משטחו של שלושה רבעים של ריבוע קטן.

משוב מעמיתים

שדה חובה*

You must be logged in to post a comment.