שברים יסודיים 3/3

הרשמה

רכישה

שברים יסודיים 3/3

- כל תלמיד יבחר שני ניירות אוריגאמי ממניפת הניירות.
- כל תלמיד יקבל שני ניירות בגודל 15ס”מ/ 15ס”מ
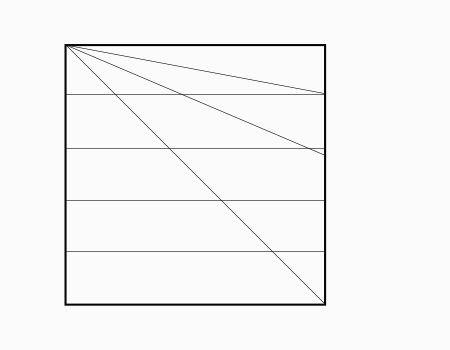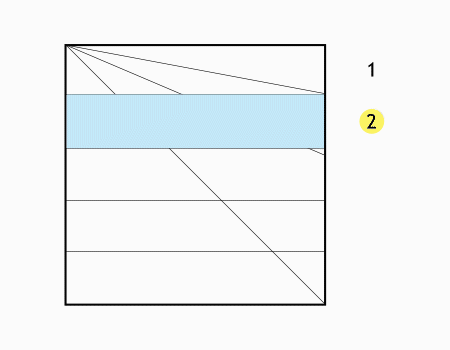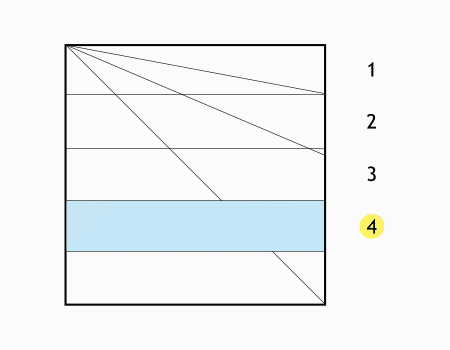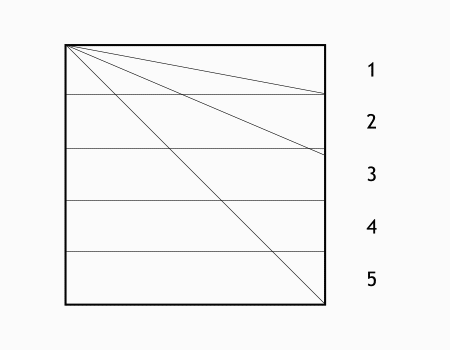
- משימה: בידקו בנייר אחד באיזה אופן אפשר לחלק נייר בצורת ריבוע ל-5 מלבנים השווים בגודלם?
- מומלץ לאפשר לתלמידים לקפל בנייר אחד ולמצוא את 5 המלבנים ורק לאחר מכן ללמד אותם את החלוקה.
- הוראת קיפול: בקיפולים הבאים נלמד לחלק נייר בצורת ריבוע ל- 5 מלבנים השווים בגודלם.
- בהוראות הבאות אנו מבקשים לסמן את הנקודות, סימון זה יסייע לתלמידים בקיפולים לכן חשוב לבקש מהתלמידים לסמן את הנקודות לפני הקיפל.
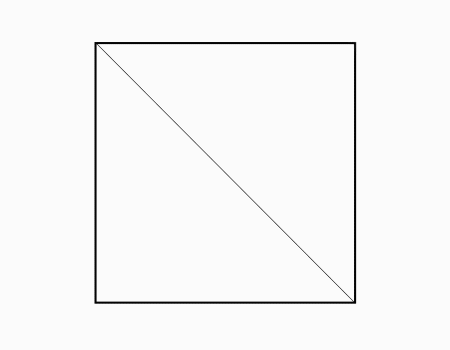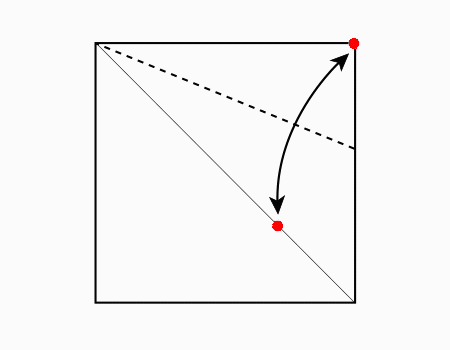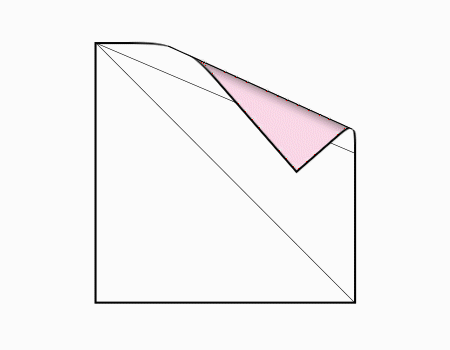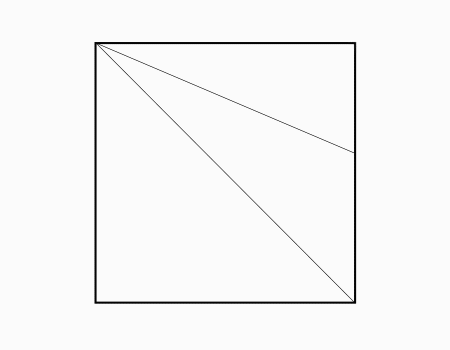
- הוראת קיפול: בנייר שעדיין לא קיפלתם לקפל קדקוד לקדקוד ולפתוח.
- הוראת קיפול: לקפל את הצלע אל קו האלכסון ולפתוח.
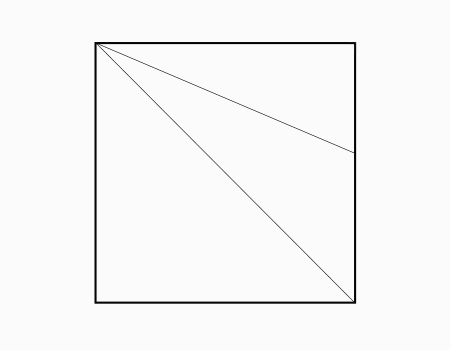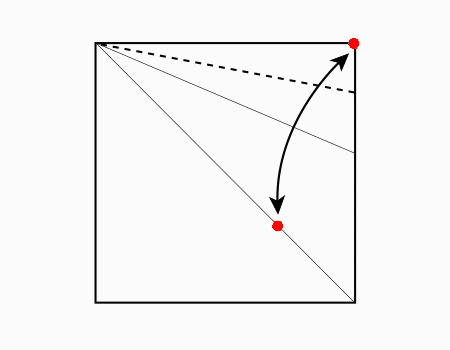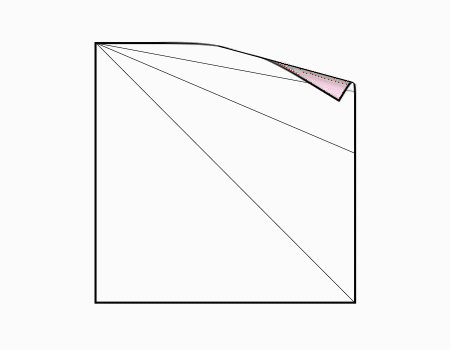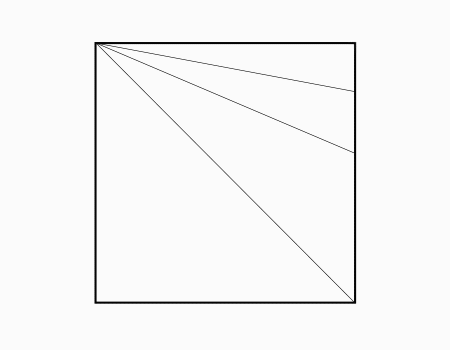
- הוראת קיפול: לקפל את הצלע אל הקו שנוצר מהקיפול הקודם כפי שמודגם באנימציה ולפתוח בחזרה..
- חשוב לא לגעת או לתקן את העבודה של התלמיד ולהדגים עם האנימציה או עם הנייר של המורה בלבד.
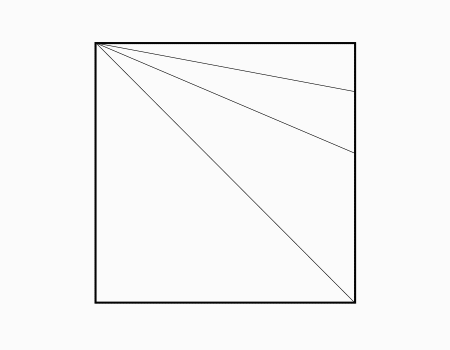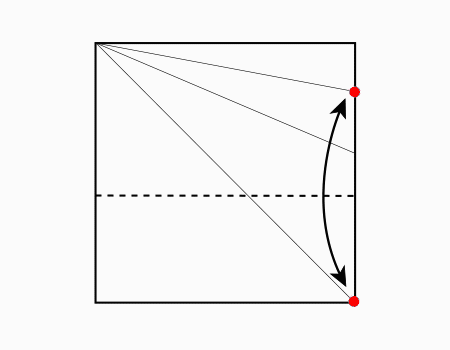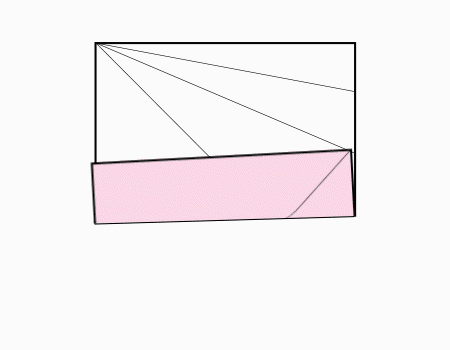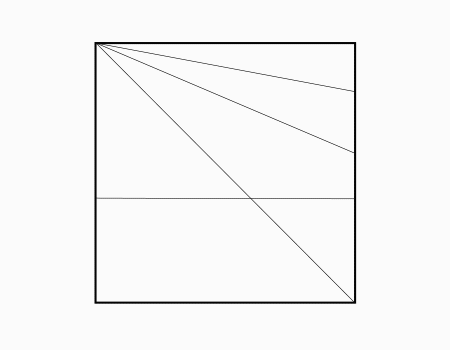
- הוראת קיפול: לסמן בנקודה כפי שמודגם באנימציה ולקפל את הצלע אל הנקודה ולפתוח.
- חשוב לא לגעת או לתקן את העבודה של התלמיד ולהדגים עם האנימציה או עם הנייר של המורה בלבד.
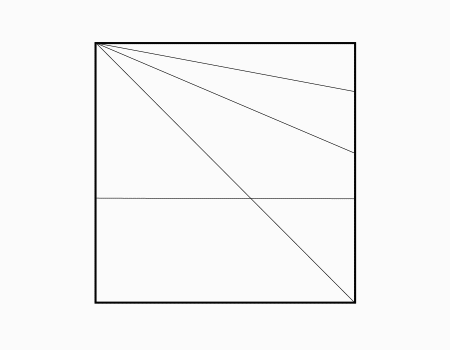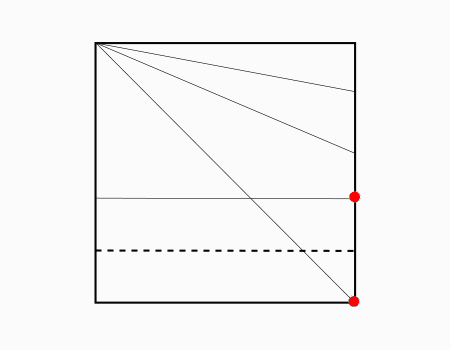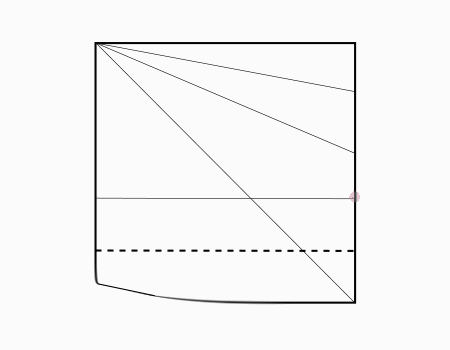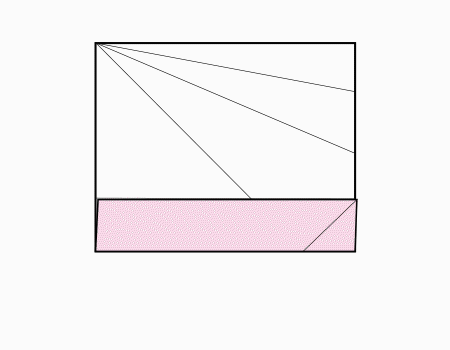
- הוראת קיפול: לסמן בנקודה את הישר שנוצר מהקיפול הקודם ולקפל את הצלע אל הנקודה. כפי שמודגם באנימציה.
- מומלץ לעבור בין התלמידים ולבדוק שקיפלו בהתאם להנחיה במידה ונדרש תיקון חשוב להדגים עם הנייר שלך ולא לגעת או לתקן את הקיפולים של התלמידים.
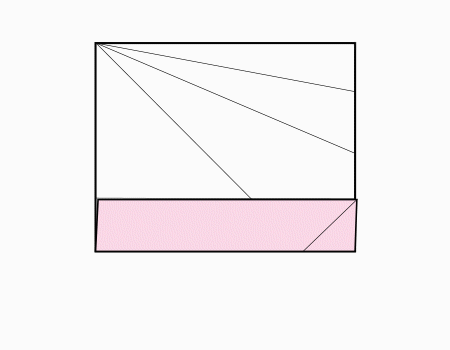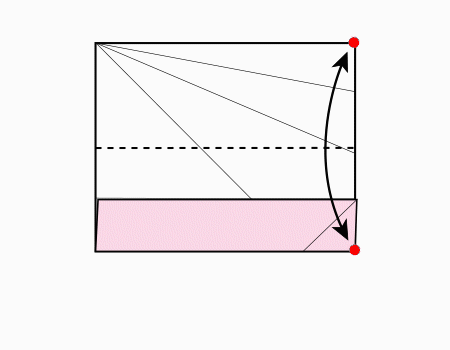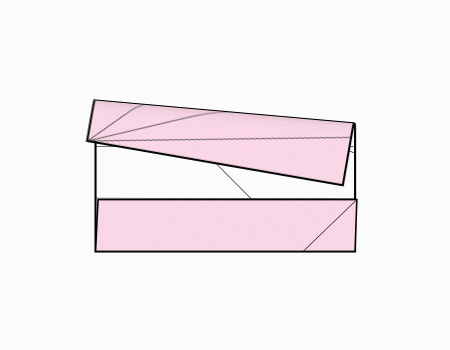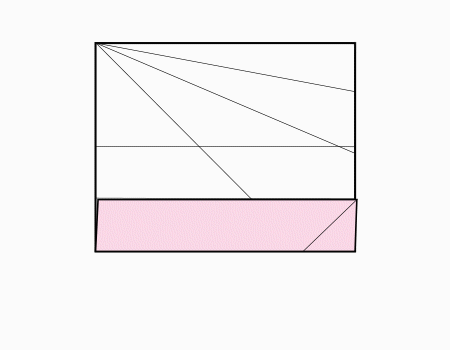
- הוראת קיפול: לקפל צלע לצלע מקבילה ולפתוח בחזרה כפי שמודגם באנימציה.
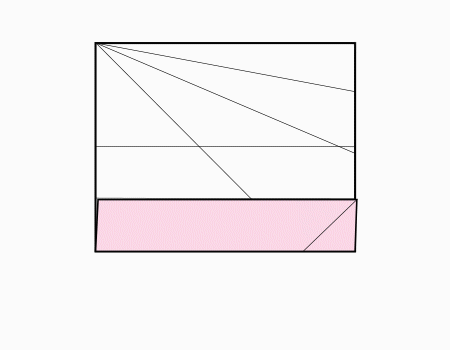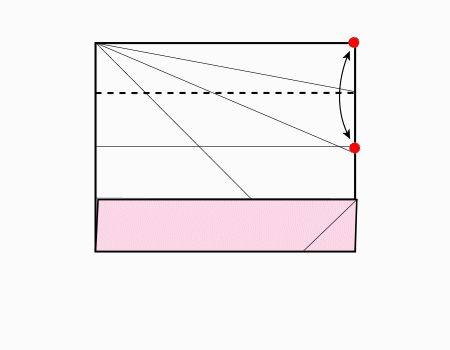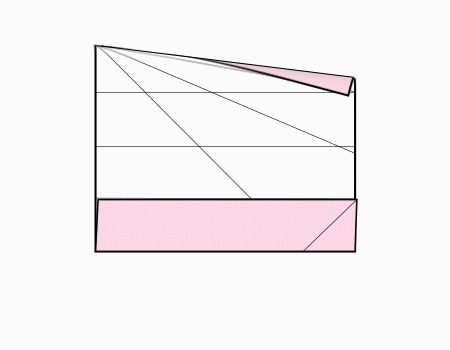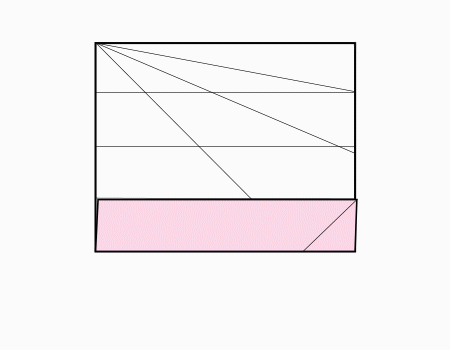
- הוראת קיפול: לקפל את הצלע לקו המסומן ולפתוח כפי שמודגם באנימציה ולפתוח בחזרה.
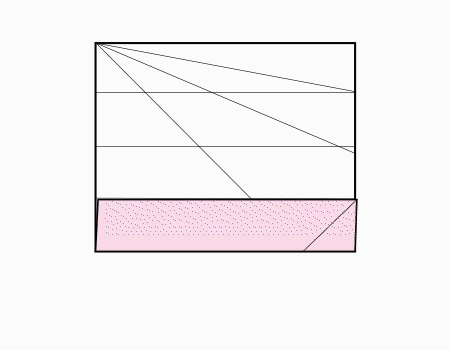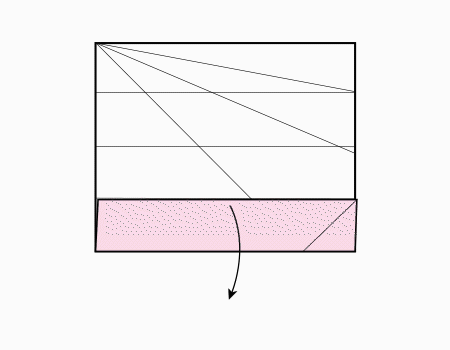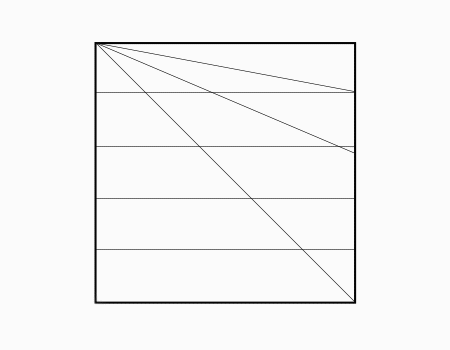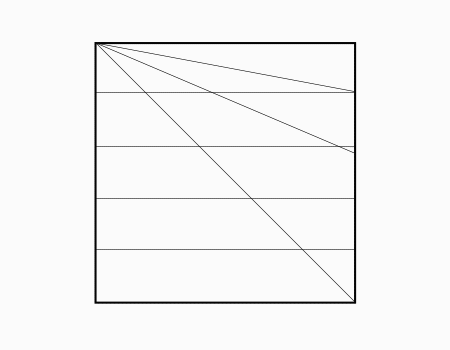
- הוראת קיפול: לפתוח את המלבן המקופל כפי שמודגם באנימציה.
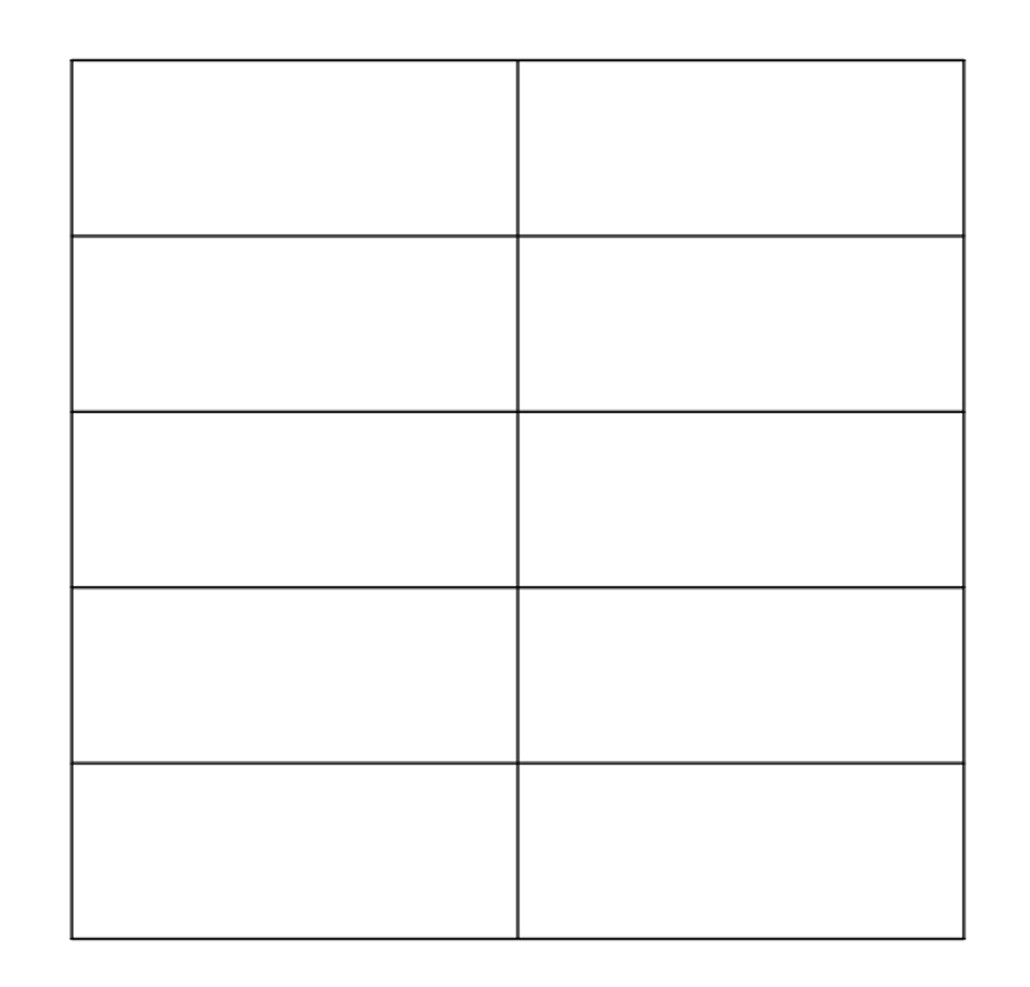
- הנייר מחולק ל- 5 מלבנים שווים.
- יש דרכים שונות לחלק נייר בצורת ריבוע ל 5 חלקים שווי שטח. כאן הדרך מדגישה בצורה ברורה ומובנת למה 5 החלקים שווה שטח מאחר שניתן לקפל את כל 5 החלקים אחד על השני ולהדגיש את שוויון השטח. ממשיכים להדגיש ש 5 במכנה של השבר היסודי 1/5מציין את החלוקה ל 5 חלקים שווי שטח וכל חלק נקרא 1/5-חמישית של השלם.
- שאלה לדיון: איזה שם ניתן לתת לכל אחד מחמשת המלבנים השווים בשטחם.
- תשובה: כל אחד מהמלבנים הוא $\dpi{120} \bg_white \frac{1}{5}$ מהריבוע השלם.
- חשוב לקשר את המכנה למספר החלקים שווי שטח שחולק הנייר השלם.
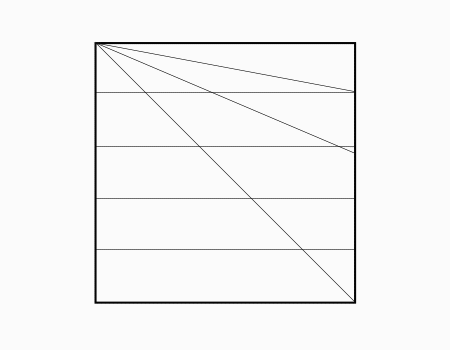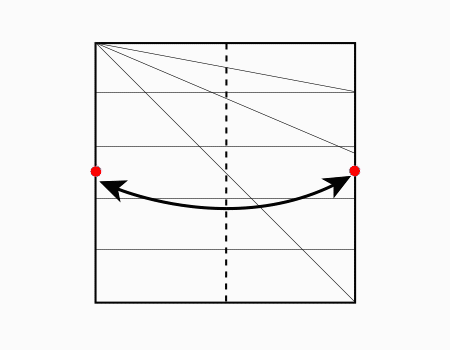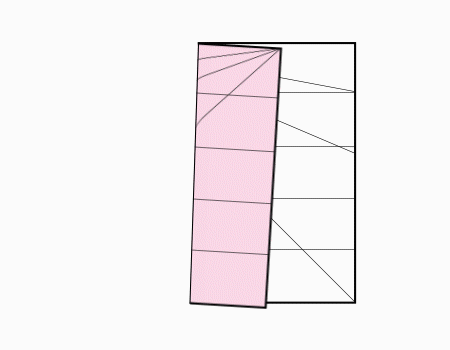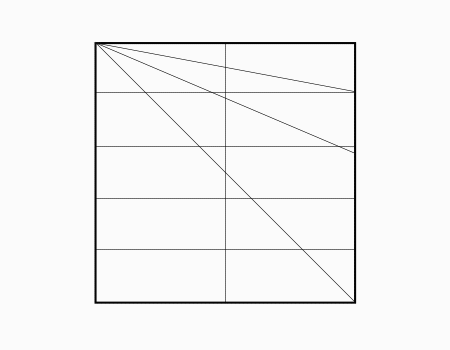
- הוראת קיפול: לקפל צלע לצלע מקבילה ולפתוח.
- שאלה לדיון: איזה שם ניתן לכל האחד מהמלבנים בחלוקת הנייר השלם למלבנים שווה שטח?
- קיפול זה מדגיש שמחלקים את נייר הריבוע לשני חלקים שווי שטח-אבל החלוקה נעשת בקו המקביל לצלע הריבוע. אם מחלקים לפי האלכסון לא חוצים כל 1/5 לשני חלקים שווה שטח. כתוצאה כל 1/5 מחולק לשני חלקים שווי שטח-בלי להשתמש בסמלים אומרים שחצי של חמישית הוא עשירית. רצוי שוב לנצל את הקיפול שניתן לקפל 10 חלקים שווי שטח אחד על השני.
- תשובה: השבר המייצג כל אחד מ עשרה המלבנים הוא $\dpi{120} \bg_white \frac{1}{10}$
- חשוב לקשר את המכנה למספר החלקים שווי שטח שחולק הנייר השלם.
- הוראת קיפול: לסובב את הנייר.
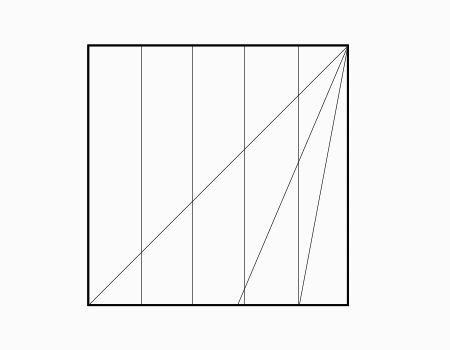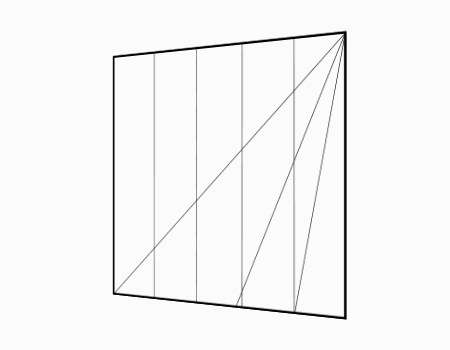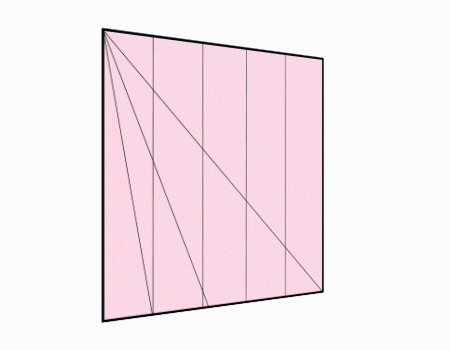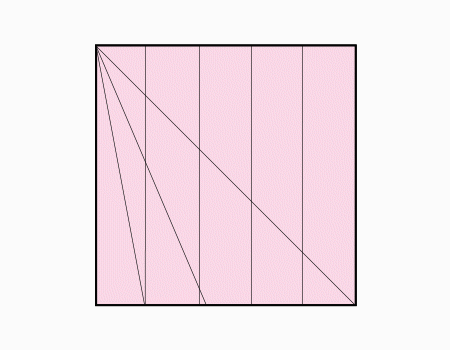
- הוראת קיפול: להפוך את הנייר לצד השני
- חשוב להדגיש שמהרגע שחילקנו את נייר הריבוע ל 5 חלקים שווי שטח לא משנה מכוונות של הנייר.
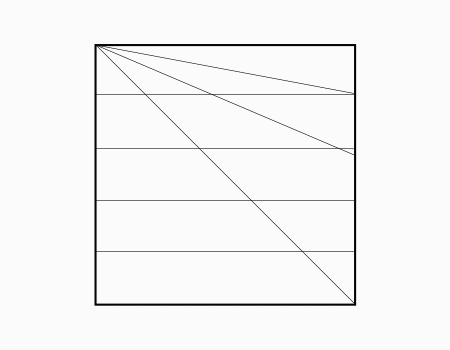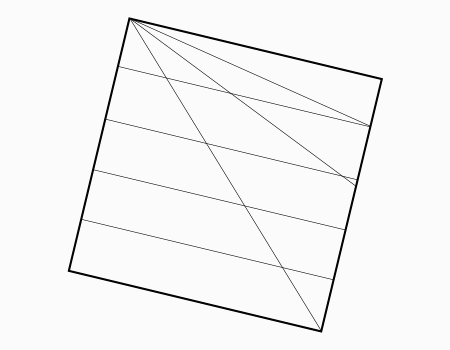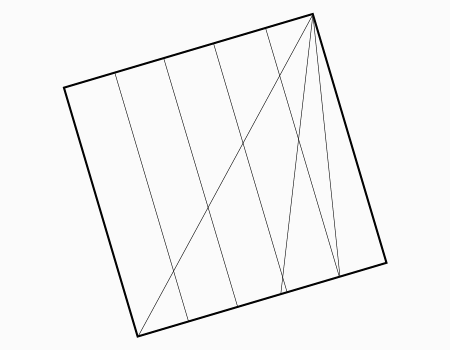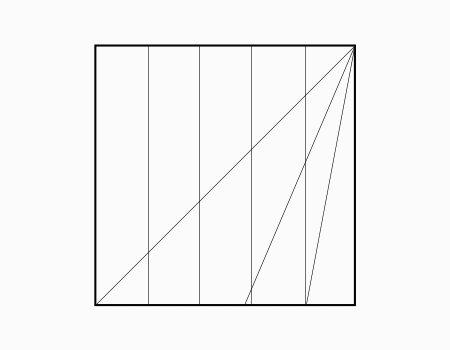
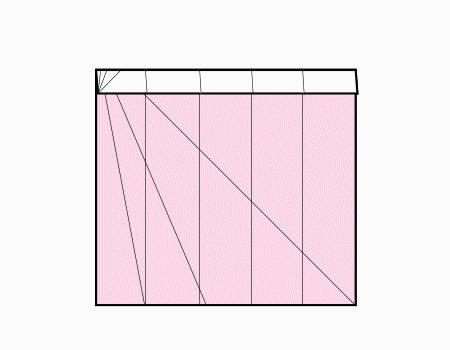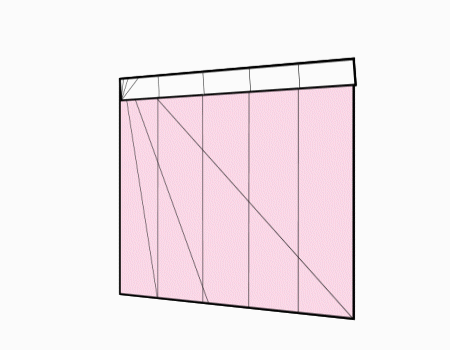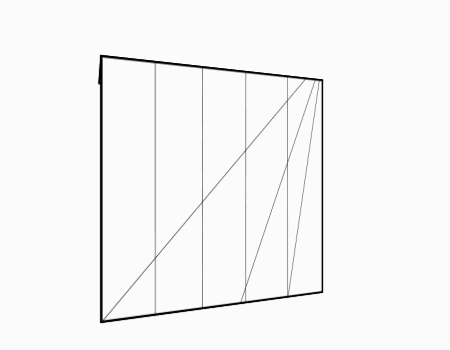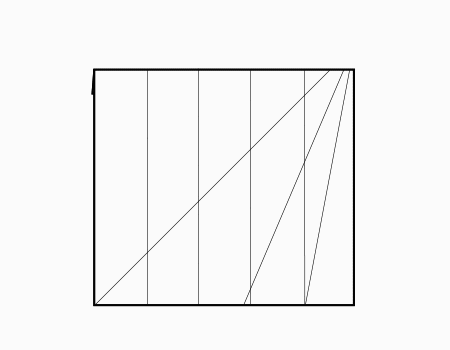
- הוראת קיפול: לשרטט את האלכסון ואת הנקודות האדומות כפי שמודגם באנימציה ולקפל את הצלע אל הנקודה האדומה. שימו לב שקיפול הצלע הוא למפגש האלכסון עם הקטע המסומן.
- מומלץ לבקש מהתלמידים לסמן את האלכסון ולמצוא את נקודת המפגש בין האלכסון לישר ולסמן בנקודות ורק לאחר מכן לקפל.
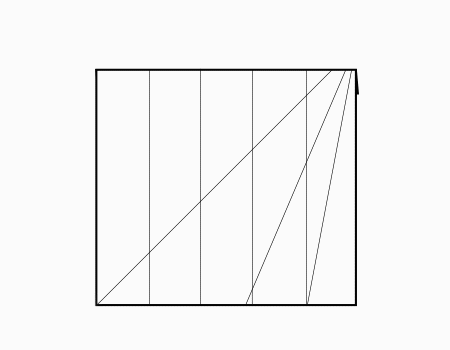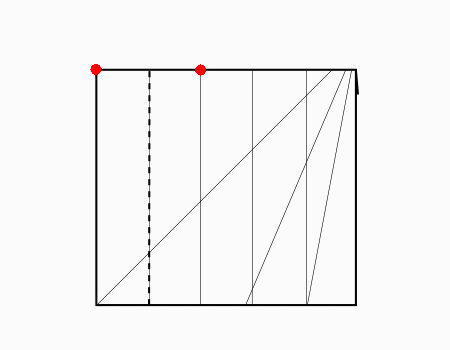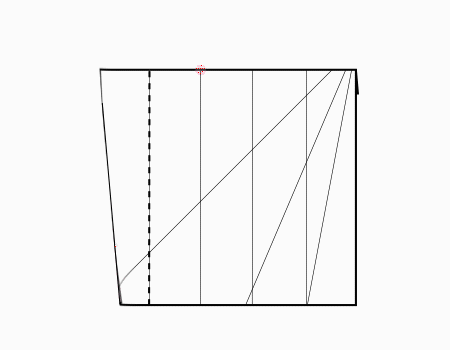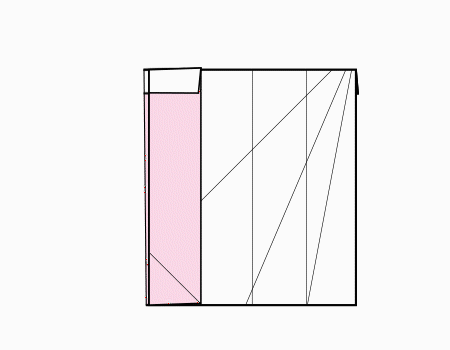
- הוראת קיפול: להפוך לצד השני כפי שמודגם באנימציה.
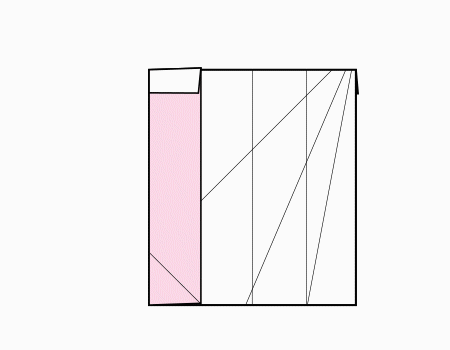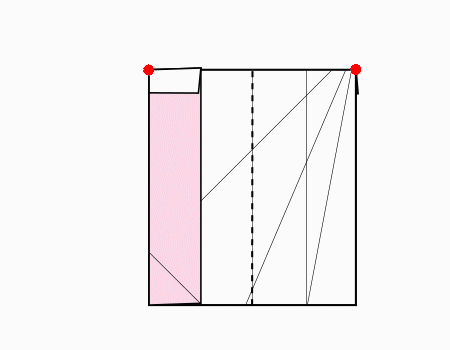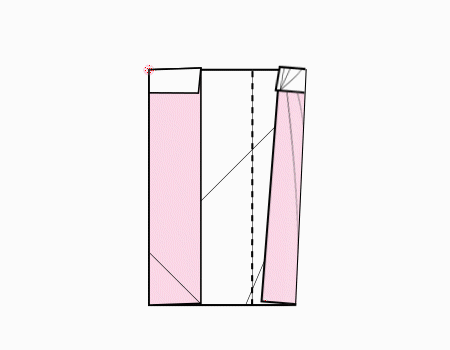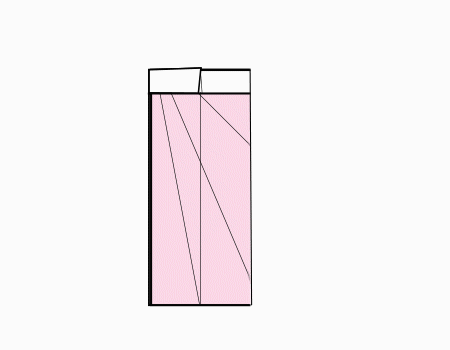
- הוראת קיפול: לקפל את הצלע לנקודה האדומה כפי שמודגם באנימציה.
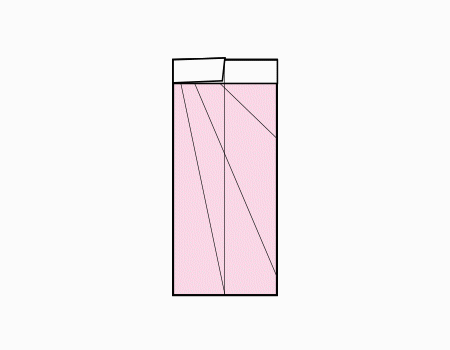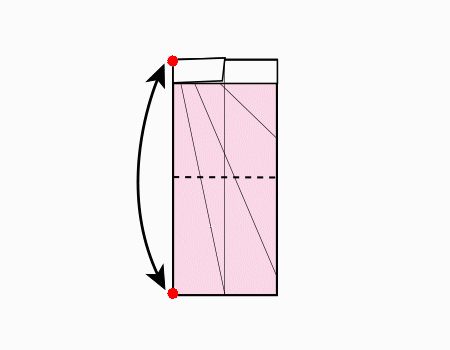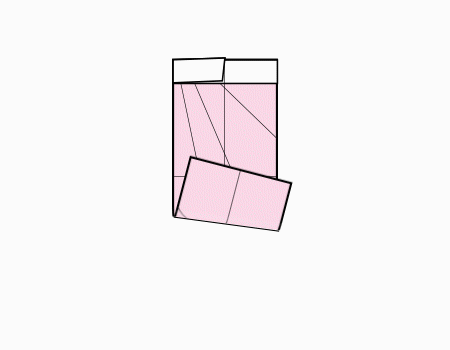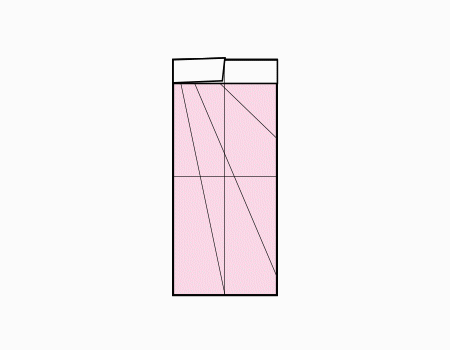
- הוראת קיפול: להכניס את הצלע מתחת למלבן הלבן כפי שמודגם באנימציה.
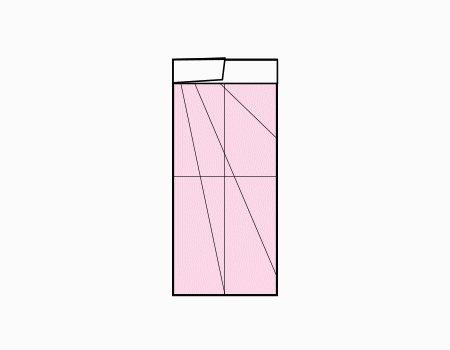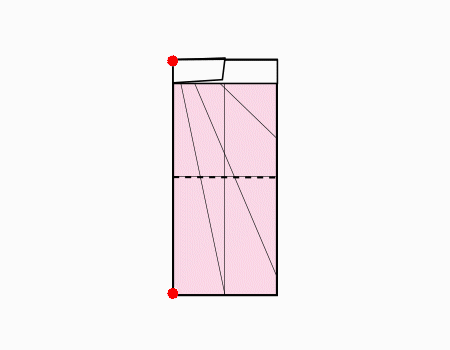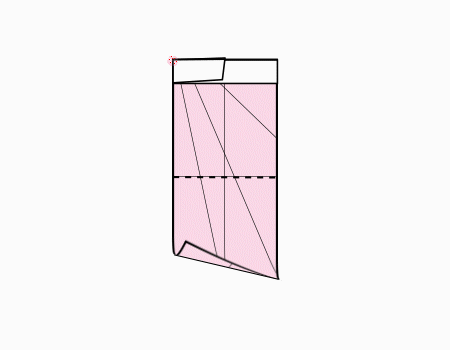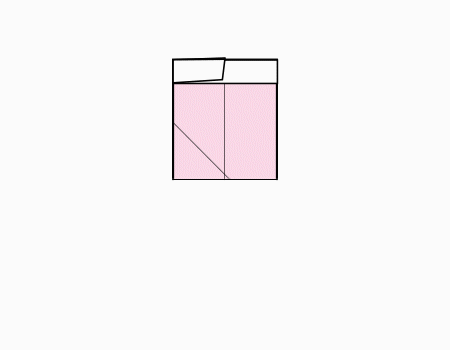
- הוראת קיפול: לקפל את הצלע הקצרה לצלע המקבילה ולפתוח כפי שמודגם באנימציה.
- הוראת קיפול: להכניס את הצלע הקצרה מתחת למלבן הלבן.
- קיפול זה נועל את השקית ולכן חשוב להדגיש לתלמידים שעליהם להכניס את הצלע מתחת למלבן הלבן.
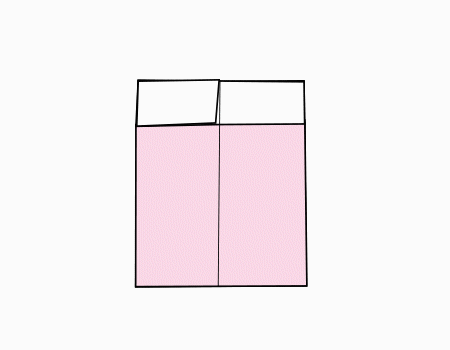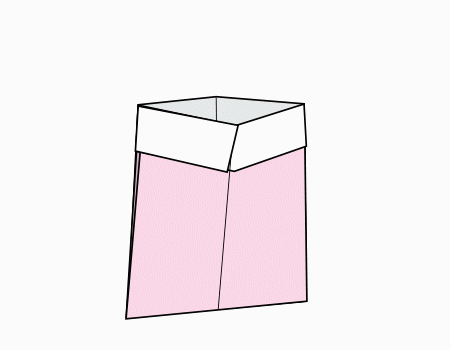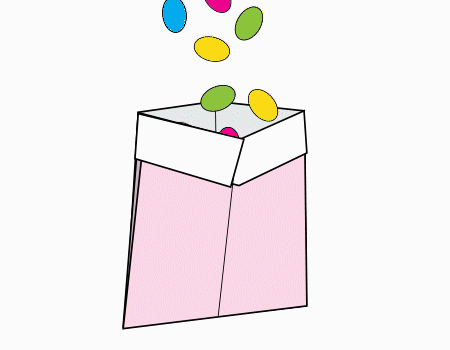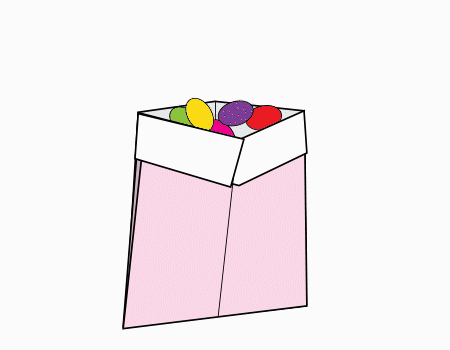
- נפתח את השקית ונוכל להכניס בה כל מה שנחפוץ.

מטרת הפעילות
- הכרת השברים היסודיים 1/5, 1/10
- הכרת השבר כחלק מהשלם.
- פעילויות מוחשיות להכרת חלקי השלם.

שם הדגם
שקית נייר למטבעות או סוכריות

מספר סידורי: 3025

שם היוצר/ת
פול ג’קסון

© כל הזכויות שמורות למרכז הישראלי לאוריגאמי

רצף מומלץ
מומלץ ללמד לפי הרצף המופיע באתר (בהתאם לתכנית הלימודים).

על השיעור
שיעור 3 מתוך 3

בקיפול התלמידים יכירו את השברים היסודיים 1/5, 1/10.

ציוני דרך
כיתה ג – שברים פשוטים עמוד 26

מילון מונחים בגאומטריה

הדגשים בהוראת השבר כחלק משלם:
1. קובעים מהו השלם (במקרה שלנו הנייר בצורת ריבוע )
2. החלקים לא חייבים להיות חופפים.
3. כאשר מונים את מספר החלקים השווים בשטחם הם לא חייבים להיות רציפים.
4. חלוקה למספר חלקים שווים בשטחם, בצורות שונות באותו שלם.
5. כאשר מציינים גודל של חלק מהשלם תמיד כדאי לכתוב ליד זה מספר החלקים שמשלימים את השלם.
6. השוואת גודלי שברים הוא תמיד ביחס לאותו שלם. – כלומר יתכן חצי של ריבוע גדול הוא גדול יותר משטחו של שלושה רבעים של ריבוע קטן.

חומרים
כל תלמיד יקבל שני ניירות בגודל 15 ס”מ/ 15 ס”מ

משוב מעמיתים

שדה חובה*

You must be logged in to post a comment.

שברים יסודיים 3/3

משוב מעמיתים

שיעורים

אודות

צור קשר