ריצוף בריבועים ובמשושים 6/6
-


-

כל תלמיד מקבל ארבעה ניירות אוריגאמי בצבעים שונים ממניפת הצבעים.
-


-

הוראת קיפול: לקפל קדקוד לקדקוד סמוך, להדק במעט את הנייר בשני הדפים ולפתוח, כפי שמודגם באנימציה.
-

-

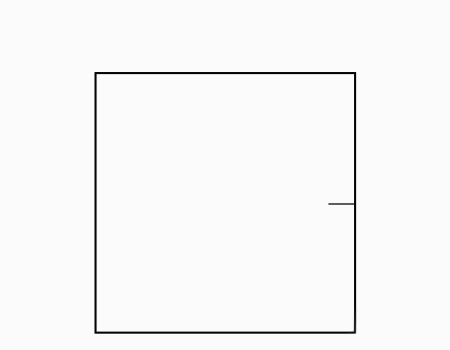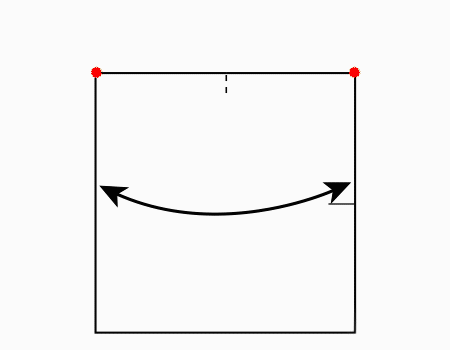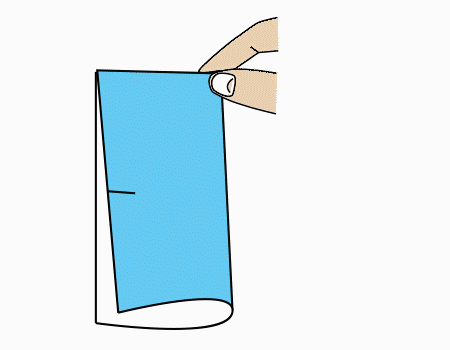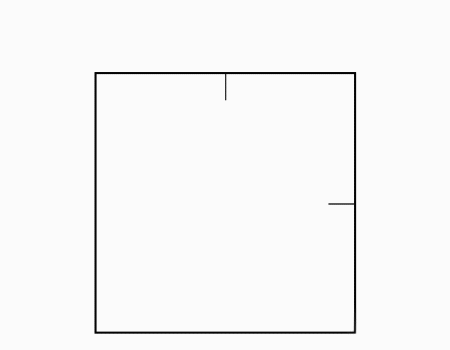
הוראת קיפול: לסובב את הנייר כפי שמודגם באנימציה.
-

-

הוראת קיפול: לקפל בשני הדפים קדקוד לקדקוד סמוך, להדק במעט את הנייר ולפתוח, כפי שמודגם באנימציה.
-


-

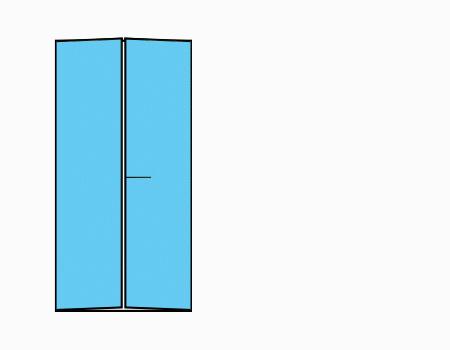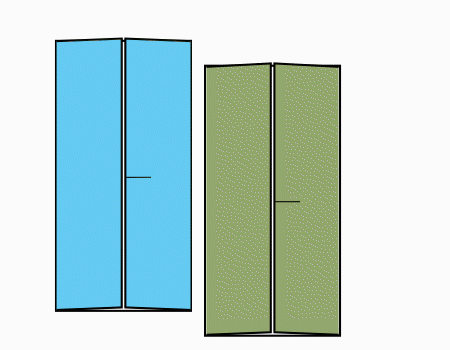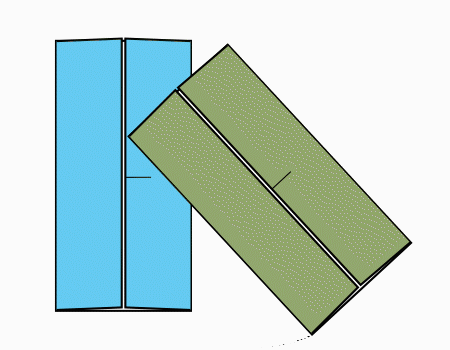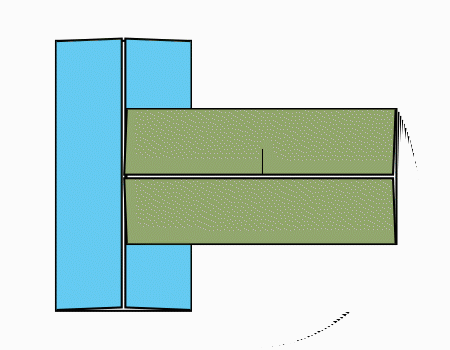
הוראת קיפול: לקפל בשני דפים כל צלע לקו שסימנו, כפי שמודגם באנימציה.
-

-

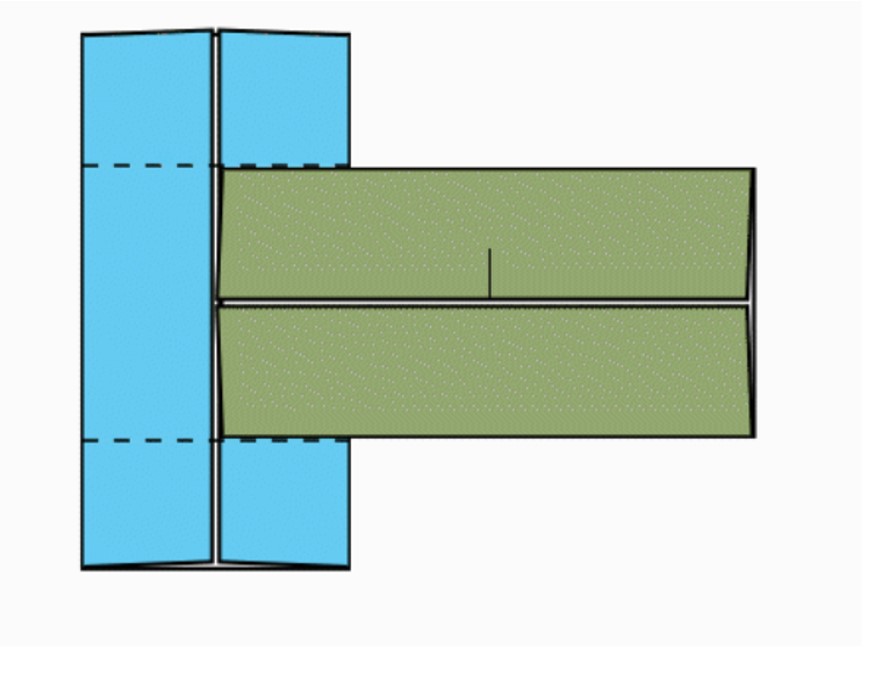
שאלה לדיון: להניח את שני הניירות שקיפלנו כפי שמודגם באנימציה.
-

-

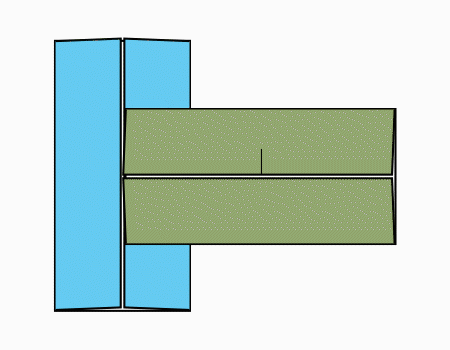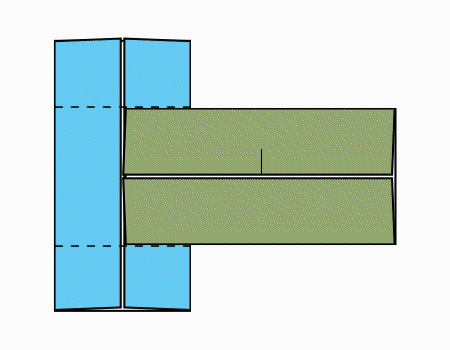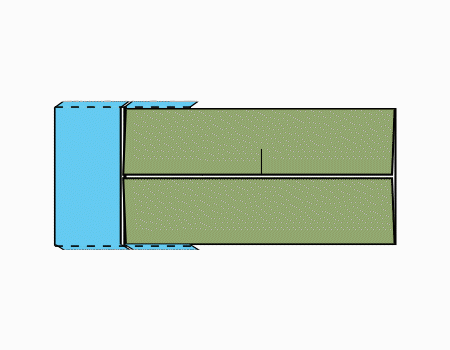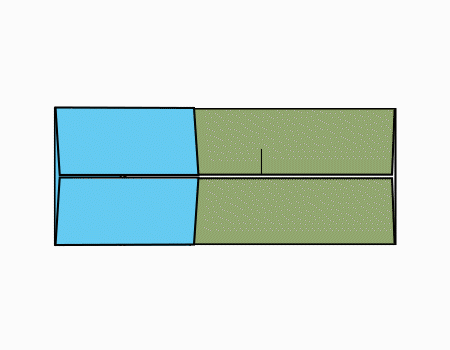
הוראת קיפול: להניח את שני המלבנים כפי שמודגם באנימציה.
-

-

הוראת קיפול: ללקפל כפי שמודגם באנימציה.קפל כפי שמודגם באנימציה.
-

-

הוראת קיפול: לקפל כפי שמודגם באנימציה.
-


-

הוראת קיפול: להפוך לצד השני
-

-

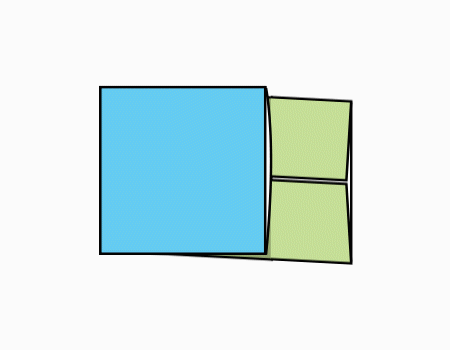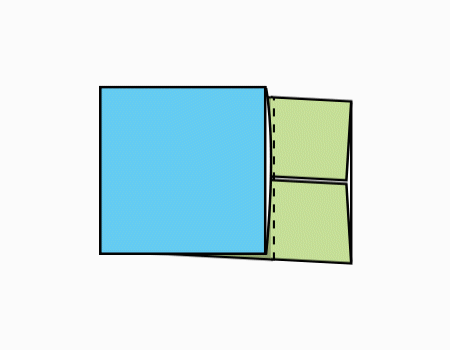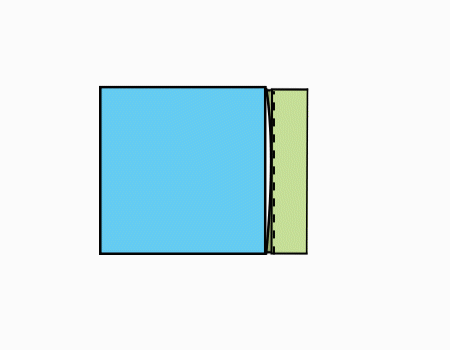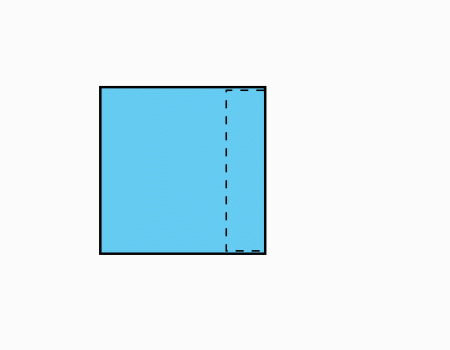
הוראת קיפול: להכניס את המלבן הירוק אל הכיס שבריבוע הכחול.
-


-

הוראת קיפול: להפוך לצד השני
-


-

הוראת קיפול: בשני ניירות נוספים, לקפל צלע לצלע מקבילה ולפתוח.
-


-

הוראת קיפול: לקפל כל צלע לקו הסימטריה ולפתוח. (בשני הדפים).
-

-

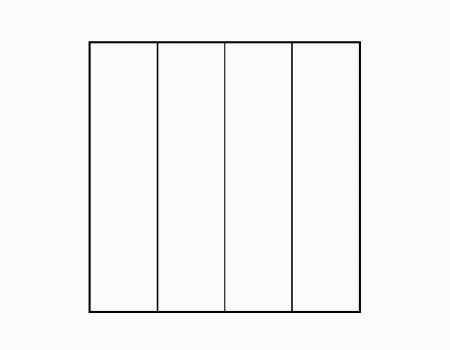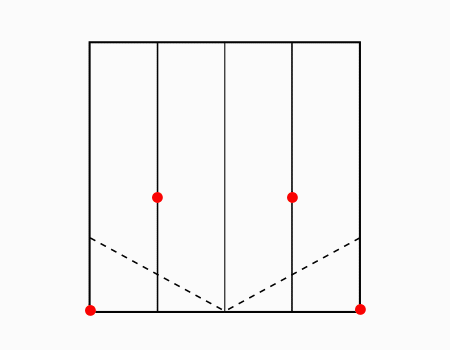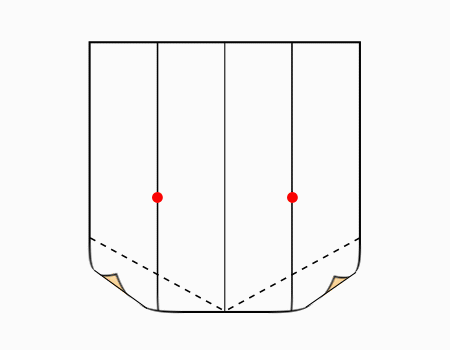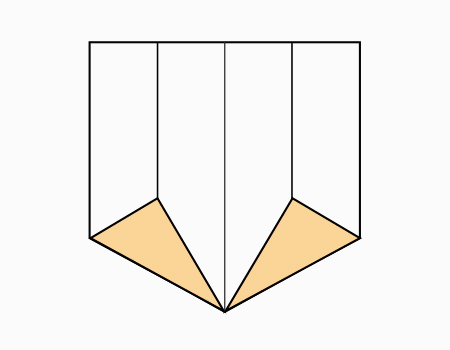
הוראת קיפול: לקפל כל קדקוד מסומן אל הנקודה המסומנת. (בשני הדפים).
-

-

-

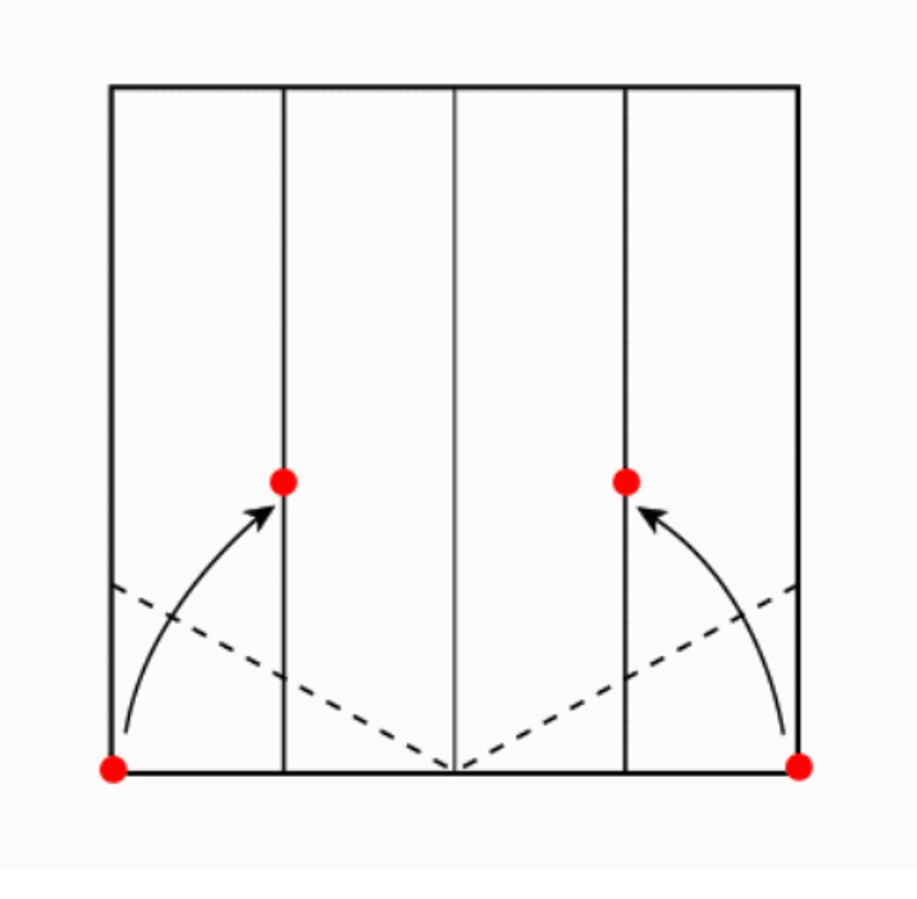
הוראת קיפול: לקפל כל קדקוד מסומן אל הנקודה המסומנת. (בשני הדפים).
-

-

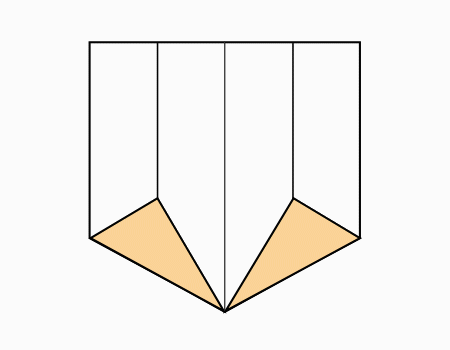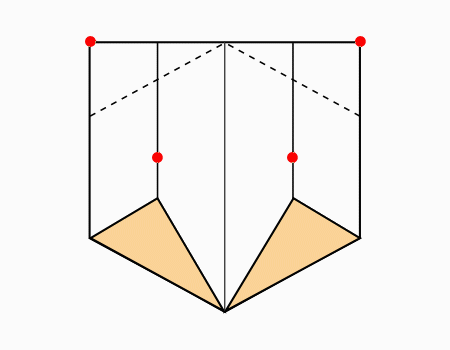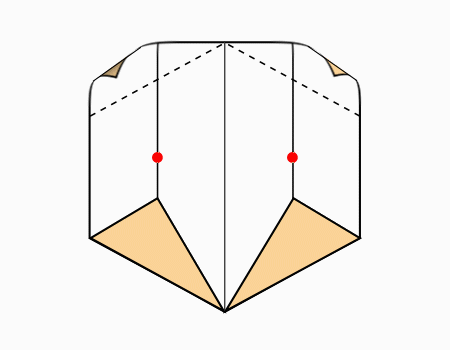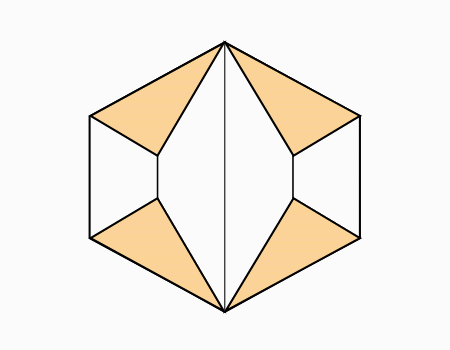
הוראת קיפול: לקפל כל קדקוד מסומן אל הנקודה המסומנת. (בשני הדפים).
-

-

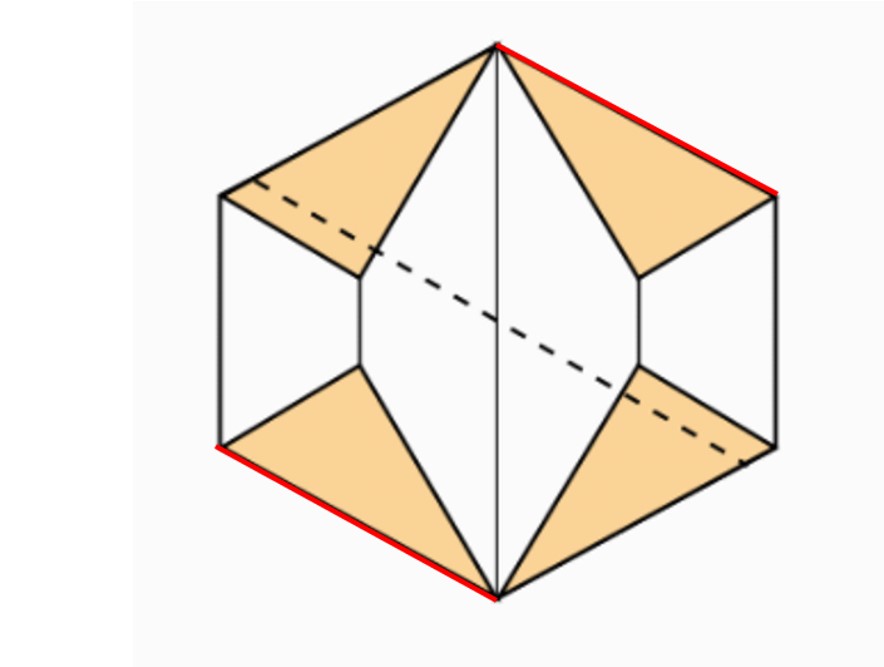
הוראת קיפול: לקפל צלע המסומנת באדום אל הצלע המקבילה המסומנת באדום. (בשני הדפים).
-

-

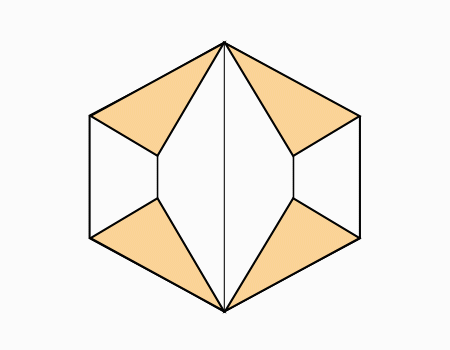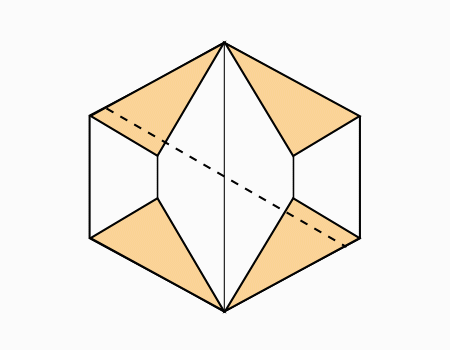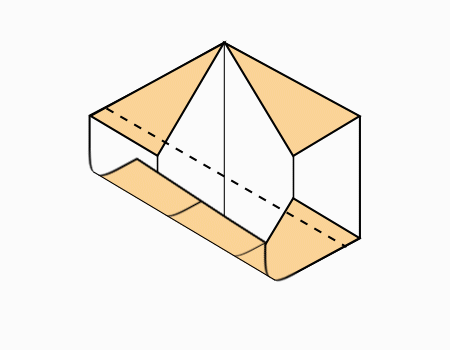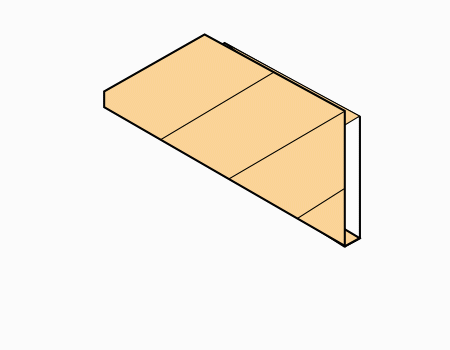
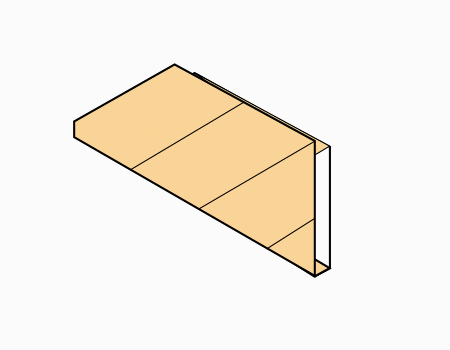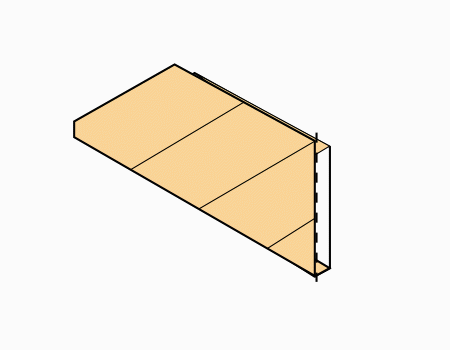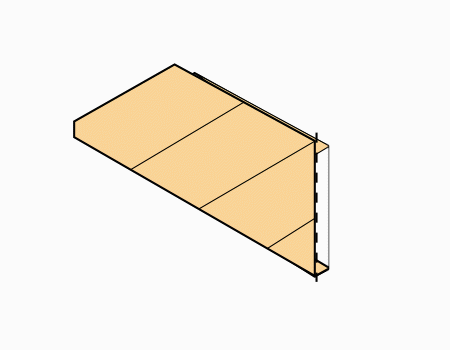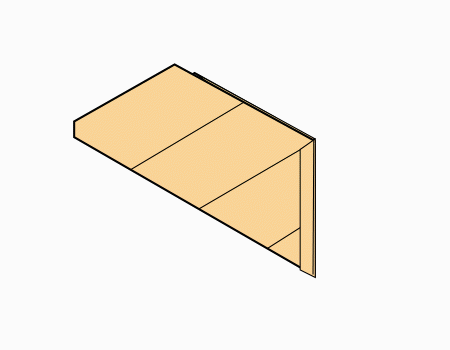
הוראת קיפול: לקפל צלע אל הצלע המקבילה כפי שהודגם בשלב הקודם (בשני הדפים).
-

-

הוראת קיפול: לקפל כפי שמודגם באנימציה (בשני הדפים).
-

-

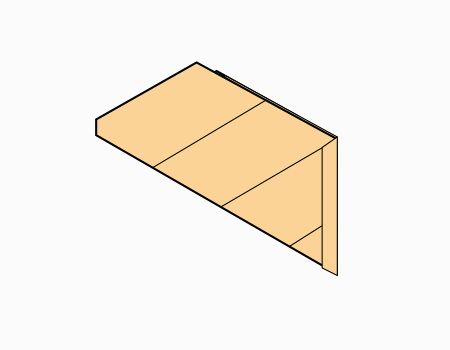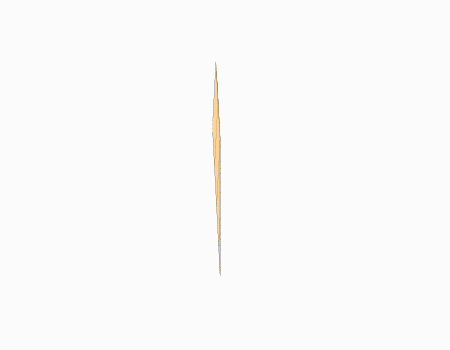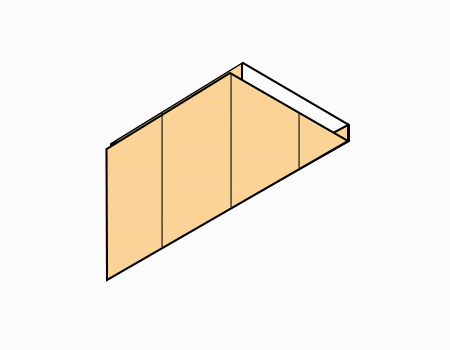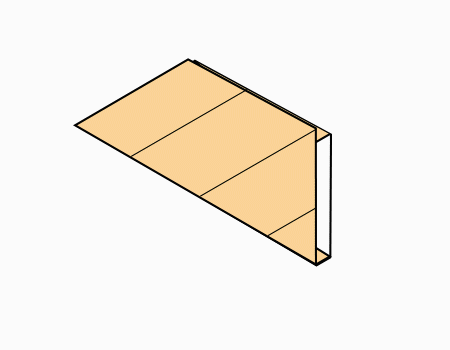
הוראת קיפול: להפוך לצד השני (בשני הדפים).
-
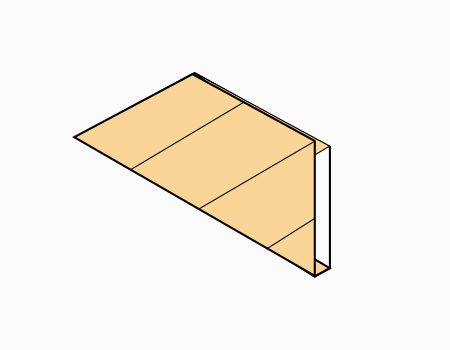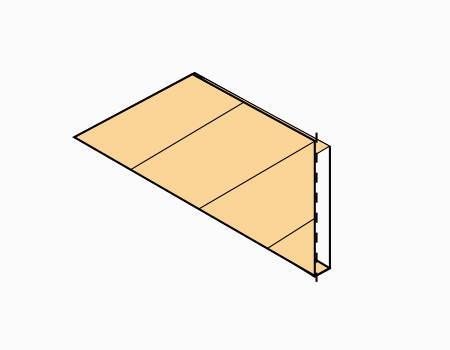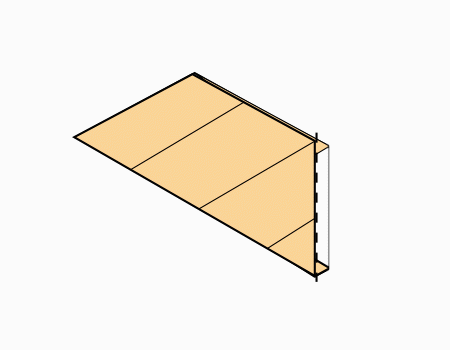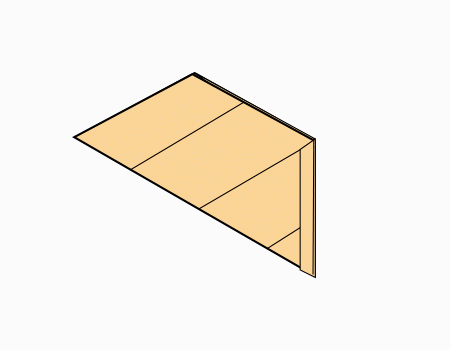

-

הוראת קיפול: לקפל כפי שמודגם באנימציה (בשני הדפים).
-
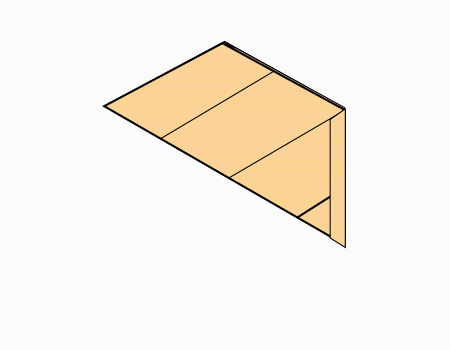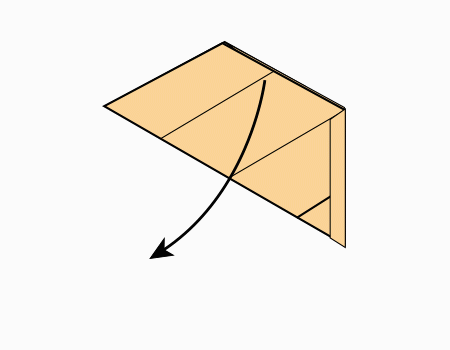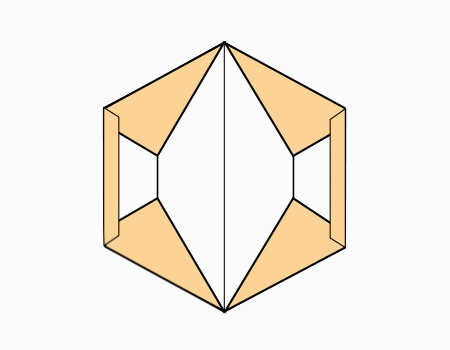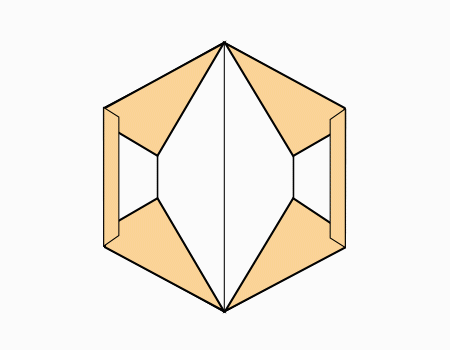

-

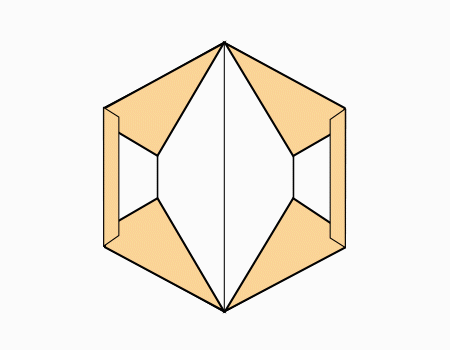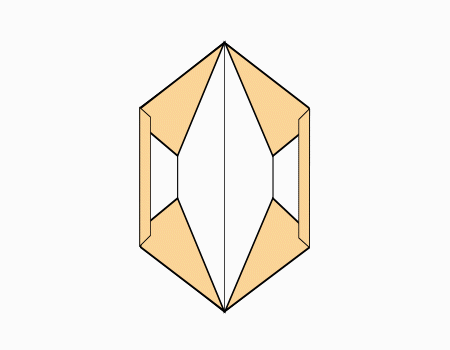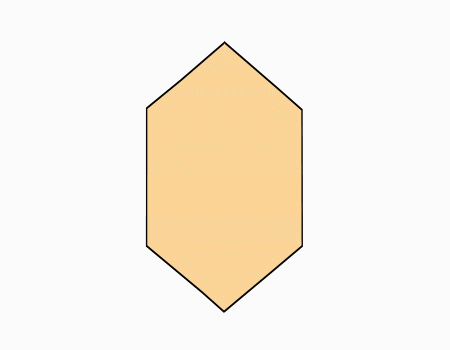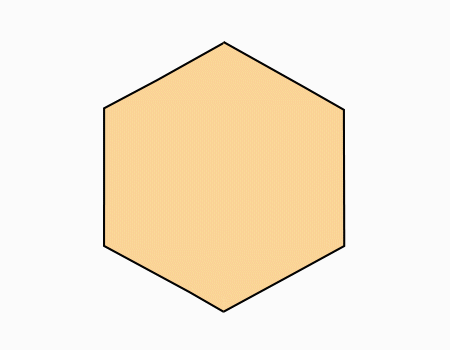
הוראת קיפול: לפתוח את הקיפול כך שיתקבל משושה (בשני הדפים).
-

-

הוראת קיפול: להפוך לצד השני (בשני הדפים).
-


-

שאלה לדיון: בידקו את מידות אורכי הצלעות במשושה, העזרו במודד. מה גיליתם לגבי המידות של אורכי הצלעות? הסבירו
-


-

תשובה: כל צלע במשושה מידת האורך שלה המידה שווה. לכן המשושה הוא משושה משוכלל.
-
במצולע משוכלל אורכי הצלעות שוות באורכן ומידת גודל הזווית שווה.

-


-

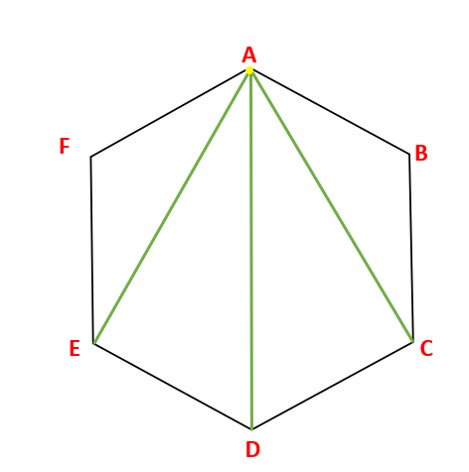
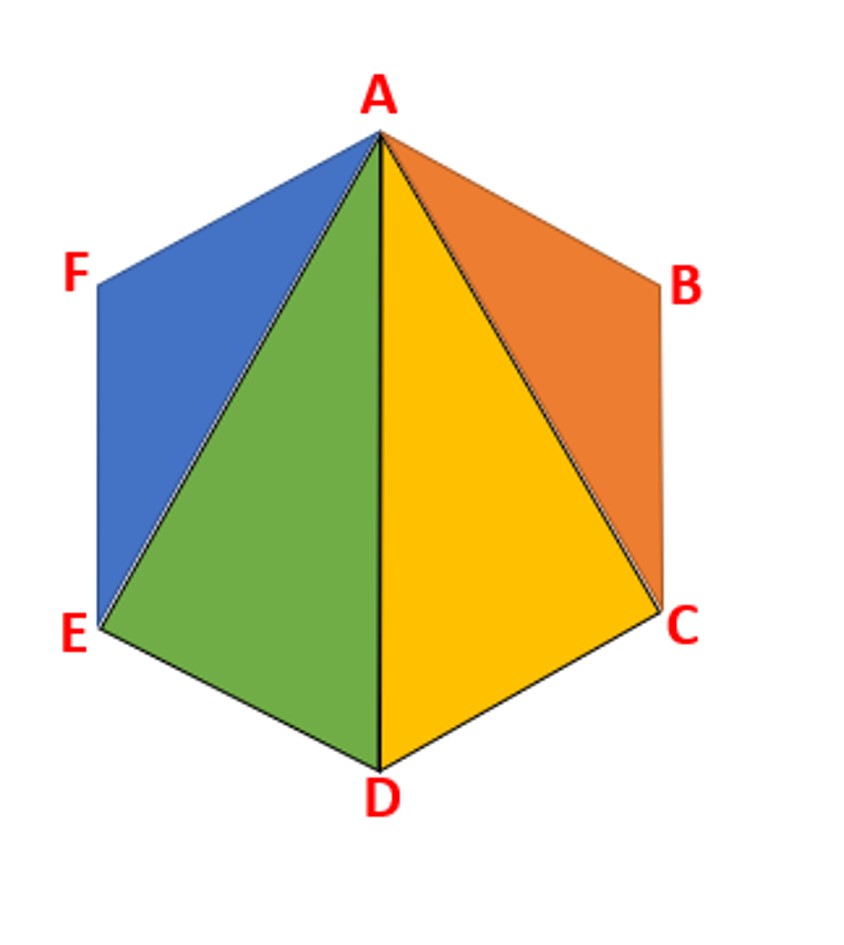
משימה: שרטטו קו (עם המודד) מהקדקוד המסומן ב- A אל כל אחד מהקדקודים שאינם סמוכים לקדקוד המסומן ב- A.
-
לבדוק על ידי שאלה האם הקדקודים שאינם סמוכים ברורים לתלמיד. (C,D,E)

-

-

שאלה 1: מנו את המשולשים המרכיבים את המשושה המשוכלל. כמה משולשים מצאתם? הסבירו שאלה 2: מהו סכום הזוויות הפנימיות של כל משולש? הסבירו שאלה 3: מהו סכום הזוויות הפנימיות במשושה ?הסבירו
-

-

תשובה 1: מצאנו 4 משולשים בתוך המשושה.
תשובה 2:סכום הזוויות הפנימיות במשולש 180°.
תשובה 3: סכום הזוויות הפנימיות במשושה הם 720°. – 4 פעמים 180° .
-
הנוסחה במציאת מספר המשולשים במצולע עם קדקוד משותף הוא n-2 כאשר n מסמנת את מספר הצלעות במצולע.

-

-

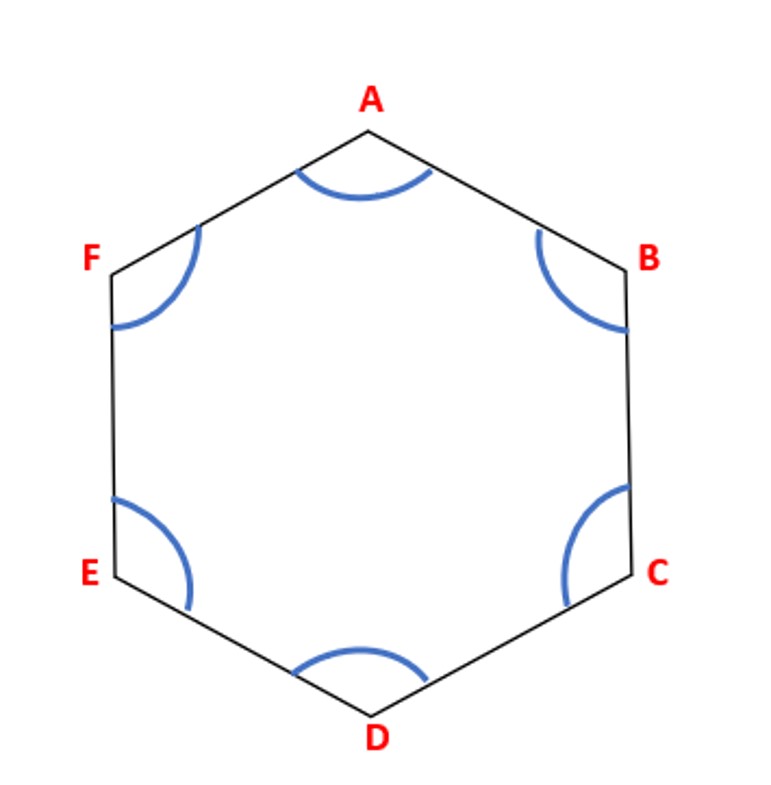
שאלה לדיון: מהו גודל כל זווית פנימית במשושה משוכלל? הסבירו איך מצאתם?
-


-

תשובה: מידת הגודל של כל זווית במשושה משוכלל היא 120°. מאחר ו- 720 לחלק ל- 6 = 120.
-
בכל מצולע משוכלל מידת הגודל של כל זווית פנימית מחשבים לפי הנוסחה

-

-

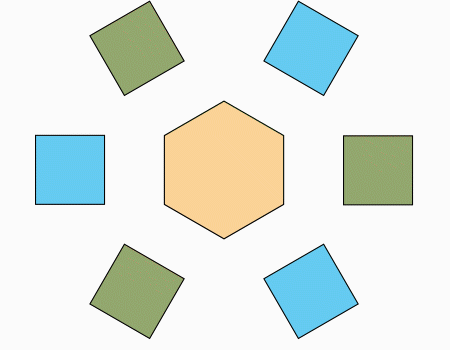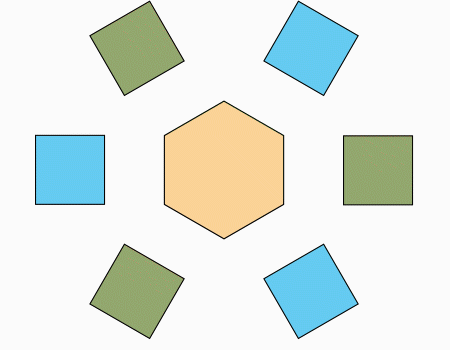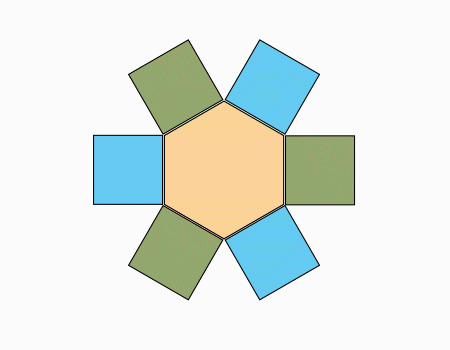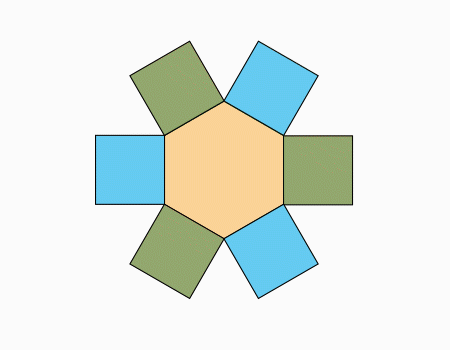
ריצוף: הניחו את המשושה ליד הריבועים כפי שמודגם באנימציה.
-


-

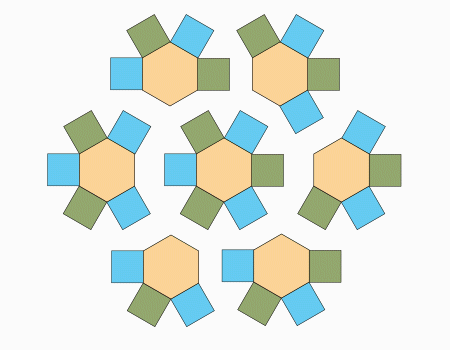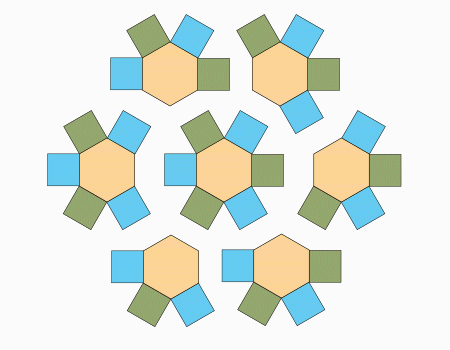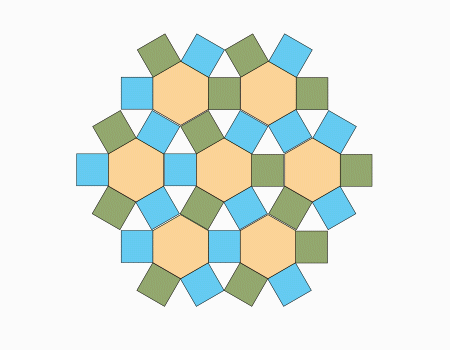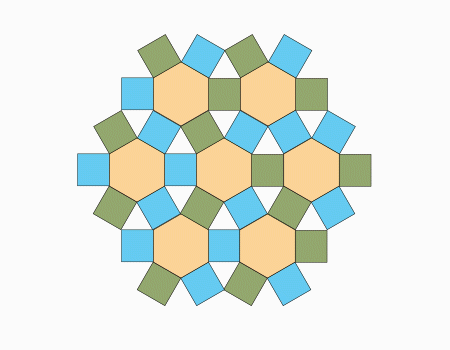
המשך ריצוף: המשיכו לרצף, כפי שמודגם באנמציה.
-

-

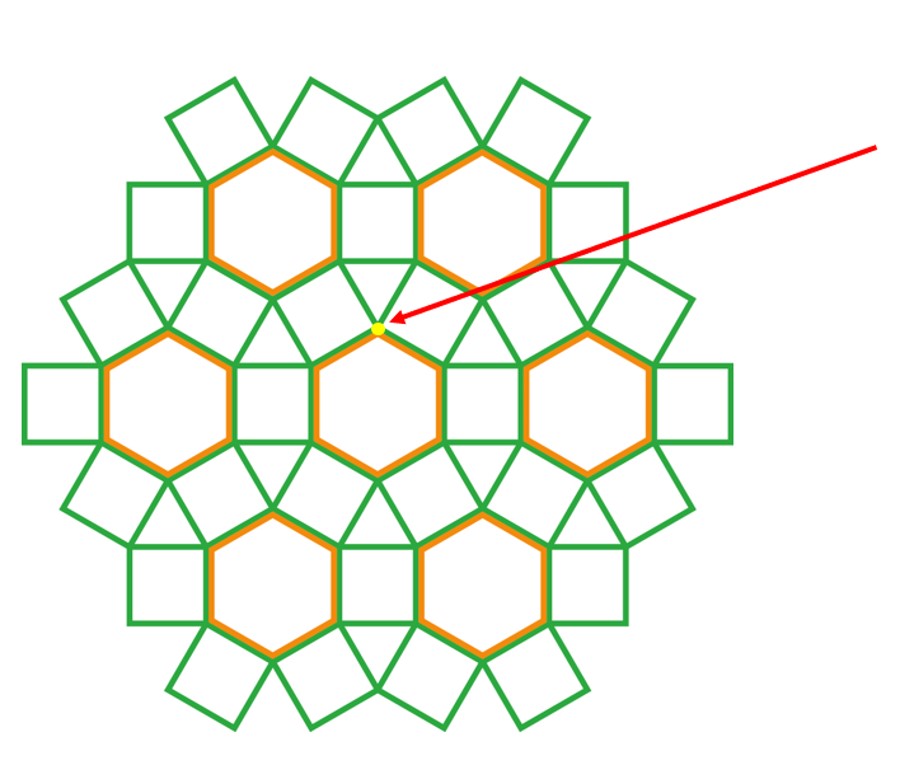
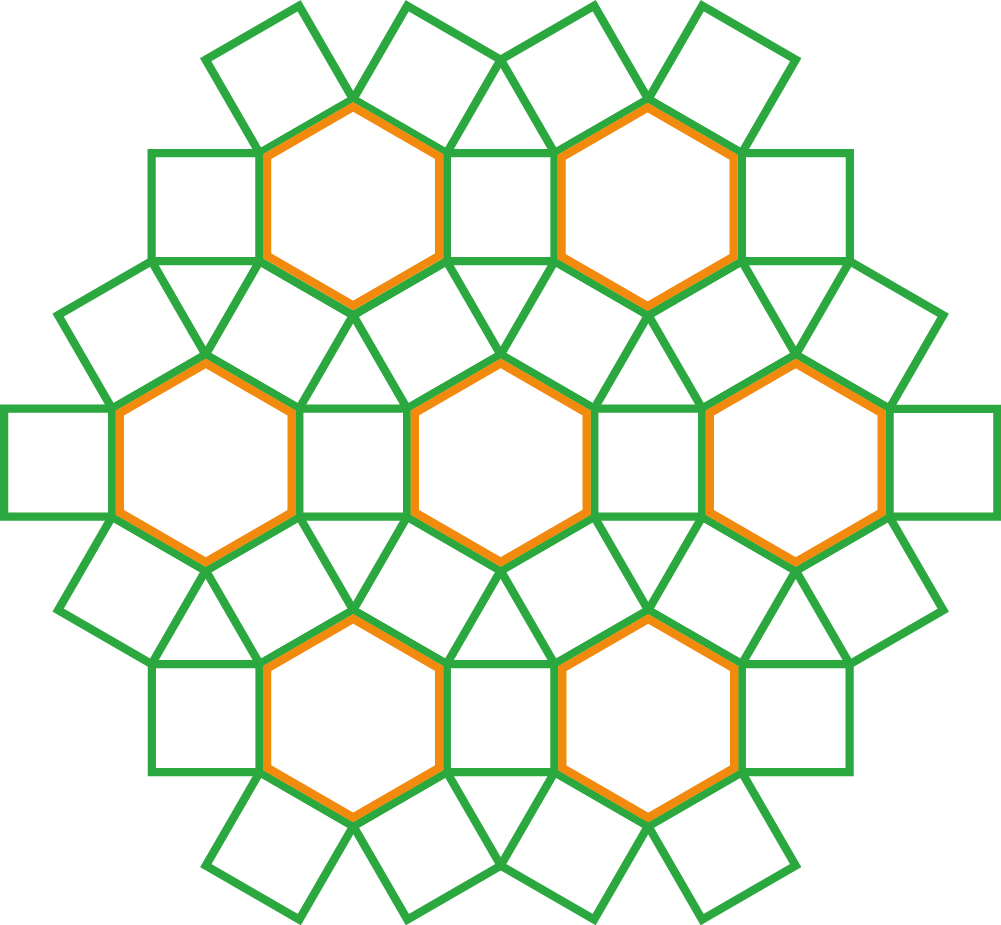
שאלה לדיון: סביב לקדקוד המשותף המסומן בצהוב יש 4 מצולעים, שני ריבועים, משולש שווה צלעות ומשושה משוכלל. מהו סכום הזוויות הפנימיות של המצולעים עם הקדקוד המשותף. (מסומן בצהוב)?
-

-

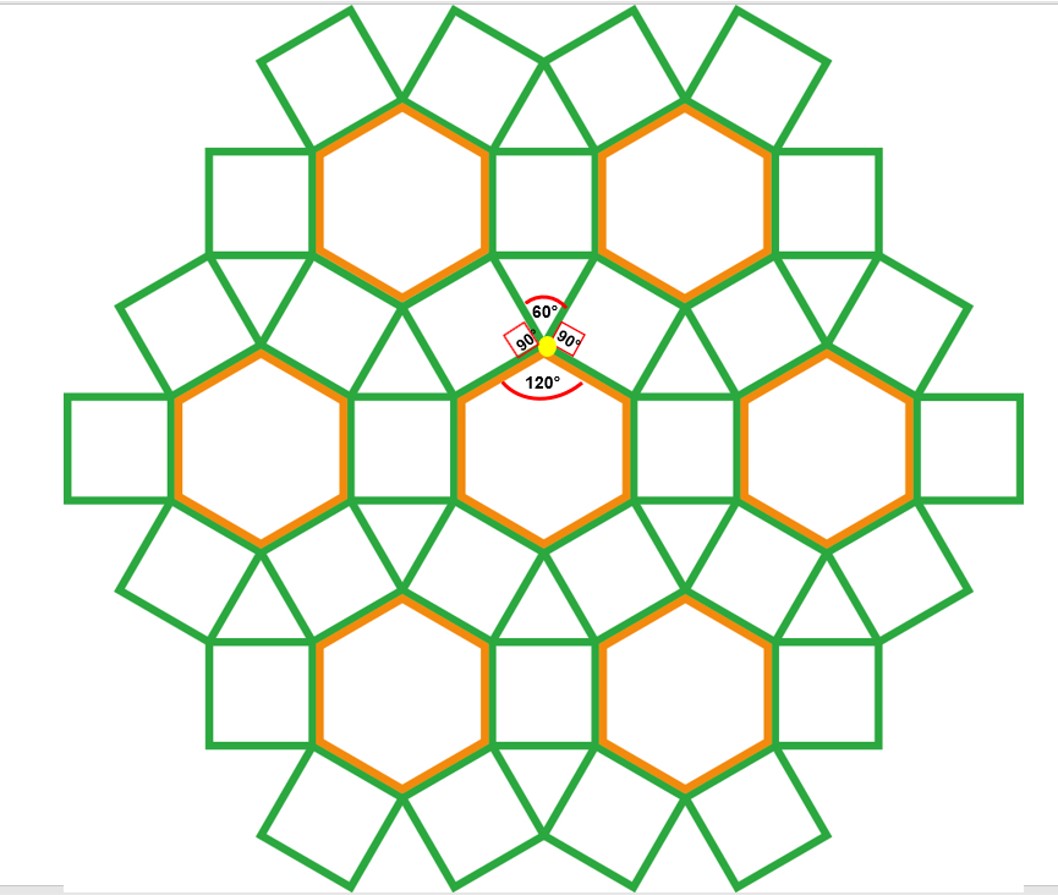
תשובה: מידת גודל הזוויות הפנימיות סביב הקדקוד המשותף המסומן בצהוב היא 360°. חישבנו באופן הבא: זווית אחת של המשולש שווה צלעות היא 60°. שתי פעמים 90° של שני הריבועים, וזווית בגודל 120° של המשושה המשוכלל.
-
360=2X90+60 +120

-

-

משימת סיכום: מיצאו קדקוד משותף ובידקו מהו סכום הזוויות הפנימיות של המצולעים עם הקדקוד משותף?
- מטרות הפעילות
מצולעים חופפים משוכללים – מצולעים מסוגים שונים.
- התלמידים יקפלו ריבוע ומשושה משוכלל וירצפו עם צורות אלו.
- הריצוף המוצג מקיים את הכלל של ריצוף בלי רווחים המכסים זה את זה.
- בריצוף מסוג זה סכום הזוויות של המצולעים הנפגשים בקדקוד משותף הוא תמיד 360°.
- שם הדגם
ריצוף בריבועים ומשושים
מספר סידורי: 5035
- רצף מומלץ
הרצף המומלץ ללימוד ריצוף הוא:
- ריצוף במצולעים חופפים משכוללים – מצולע מסוג אחד. (משולש שווה צלעות, ריבוע, משושה משוכלל).
- ריצוף במצולעים חופפים מסוגים שונים.
- על השיעור
התלמידים יקפלו ריבוע ומשושה יחקרו את הצורות וירצפו איתם תוך כדי העמקה בתכונות של משושה משוכלל.
בריצוף שני מצולעים משוכללים יגלו לתלמידים שסכום הזוויות הפנימיות של כל הצורות סביב הקדקוד המשותף הם 360°.
משך זמן פעילות מומלץ: 45 דקות
* משך זמן הפעילות נתון לשיקול המורה, ויכול להשתנות בהתאם לגודל ואופי הכיתה.
- ידע נדרש
- קדקודים סמוכים ושאינם סמוכים.
- הכרה וחקר מצולע משוכלל שכל צלעותיו שוות זו לזו וכל זוויותיו שוות זו לזו.
- הכרת הזוויות של הריבוע – גודל כל זווית 90°.
- הכרת משולש שווה צלעות גודל כל זווית הוא 60°.
- ציוני דרך
כיתה ה – עמוד 35

