כל תלמיד יבחר שני ניירות ממניפת הדפים. (נקפל בשני הריבועים במקביל.)

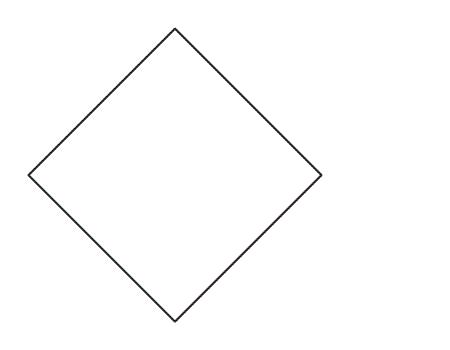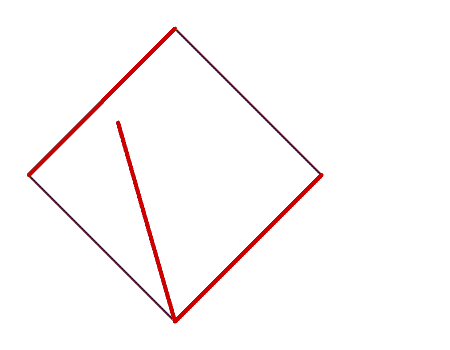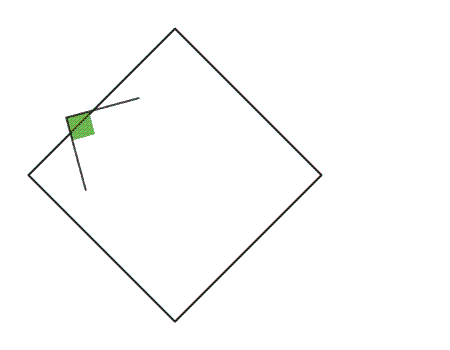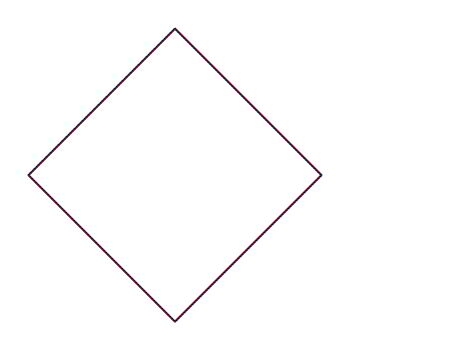
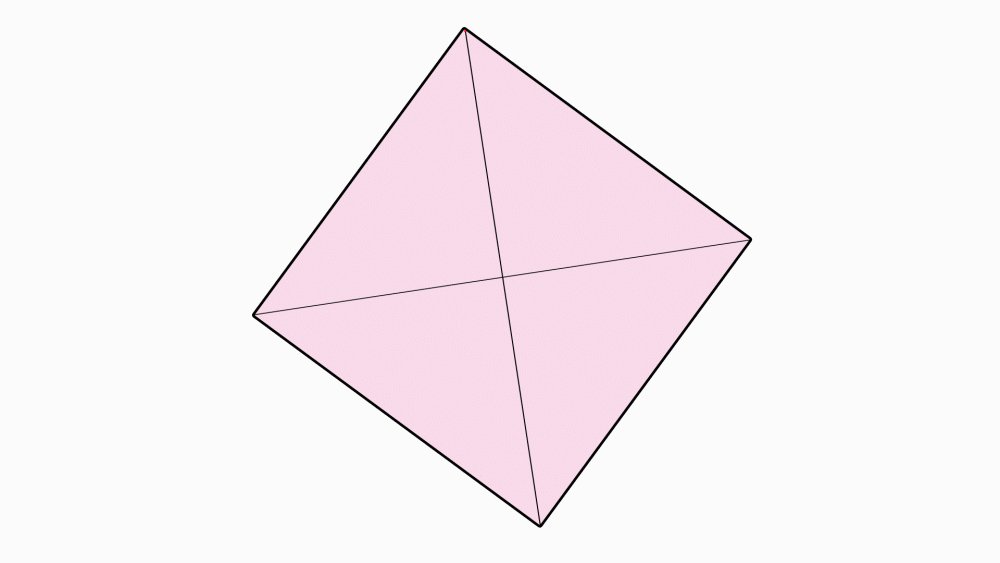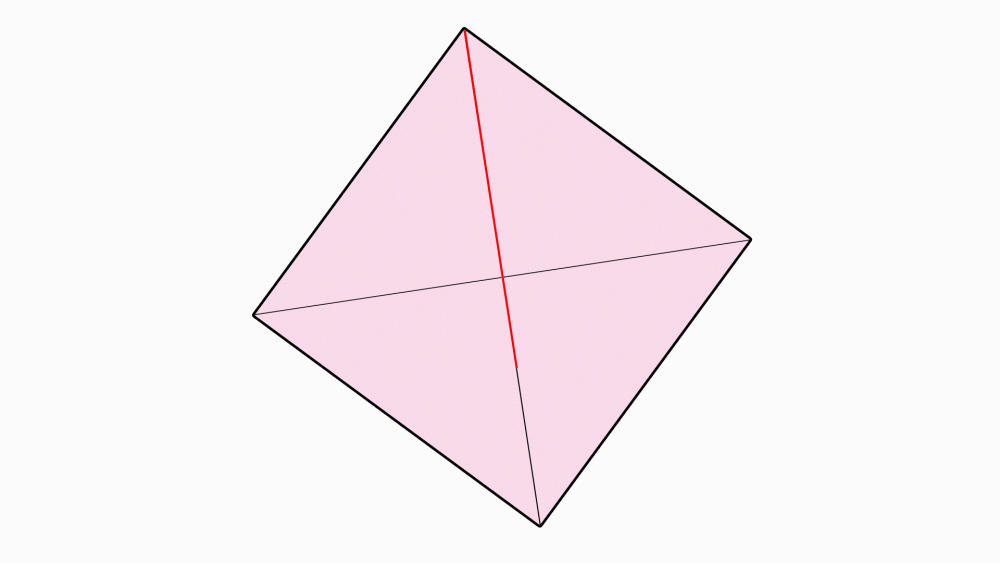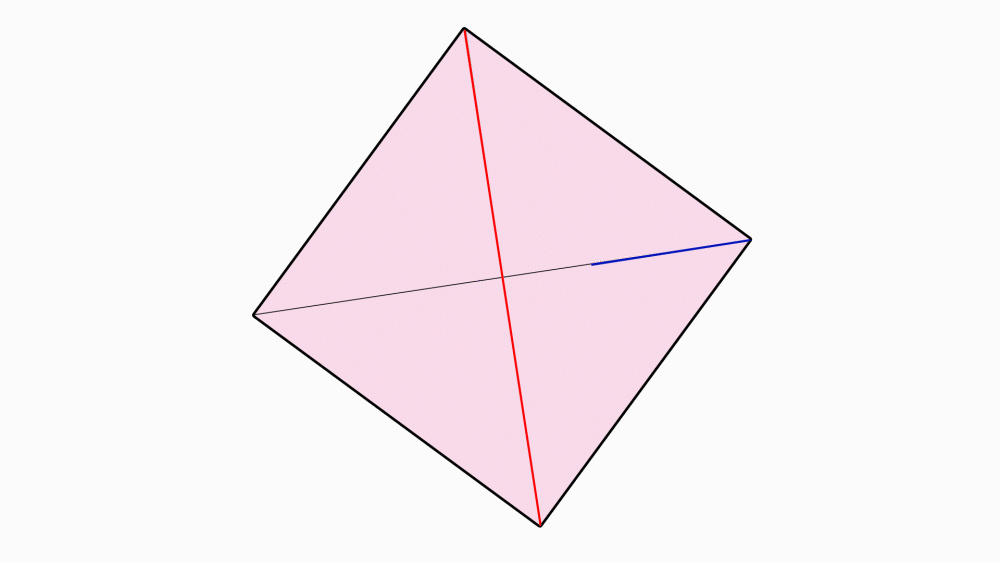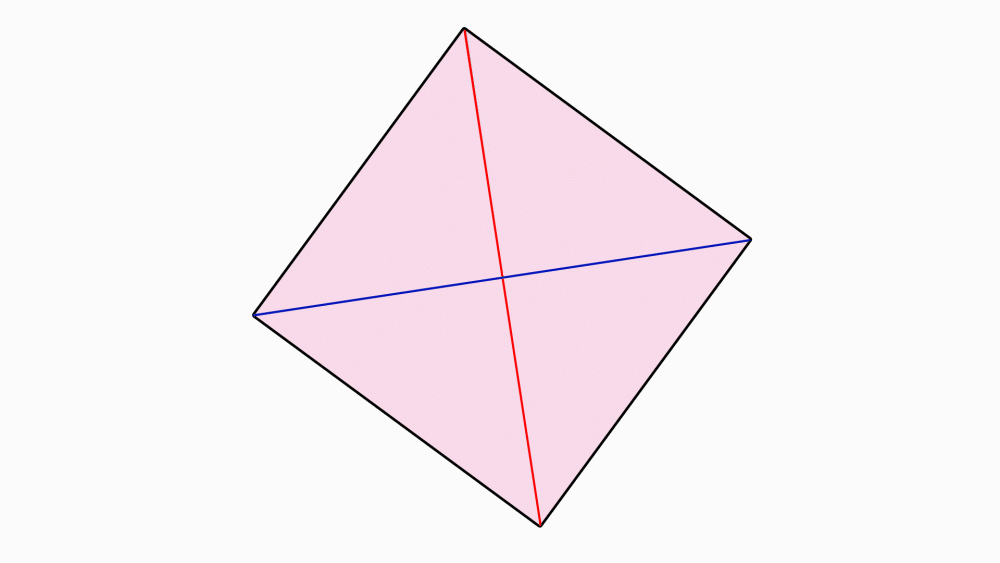
שאלה לדיון: איזה מצולע הוא הנייר שלפניכם?

תשובה: המצולע הוא בצורת ריבוע – כל צלעותיו שוות באורכן וזוויותיו ישרות.

שאלה לדיון: האם ניתן לקפל את הריבוע שקיבלתם ל- 4 משולשים חופפים ב- 2 קיפולים בלבד? נמקו.

(לקפל בשני הריבועים במקביל.)

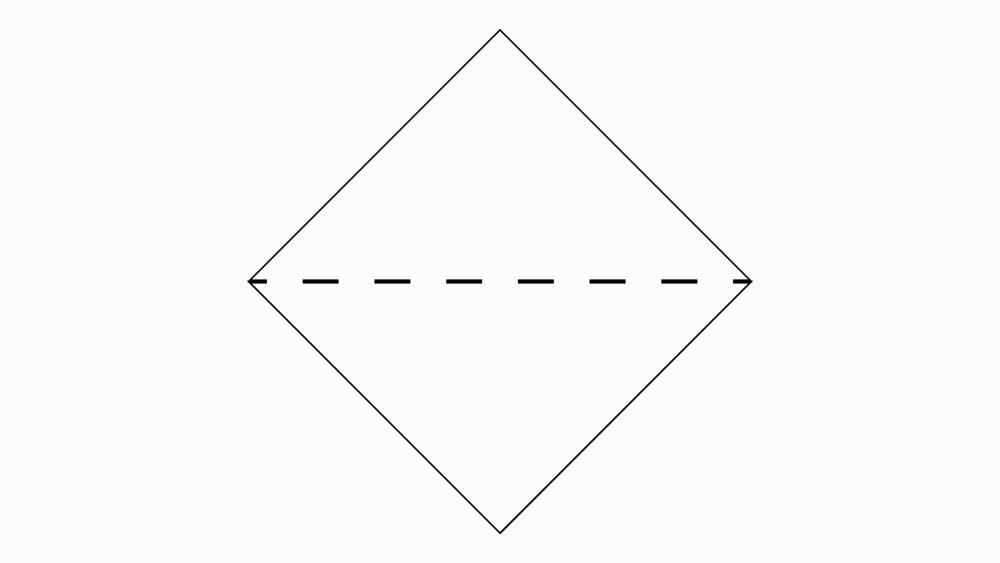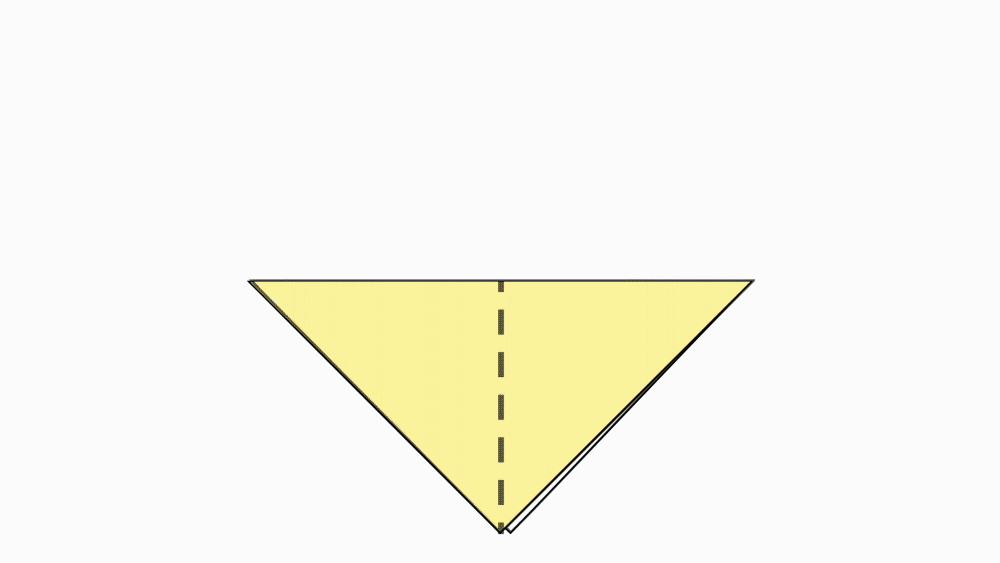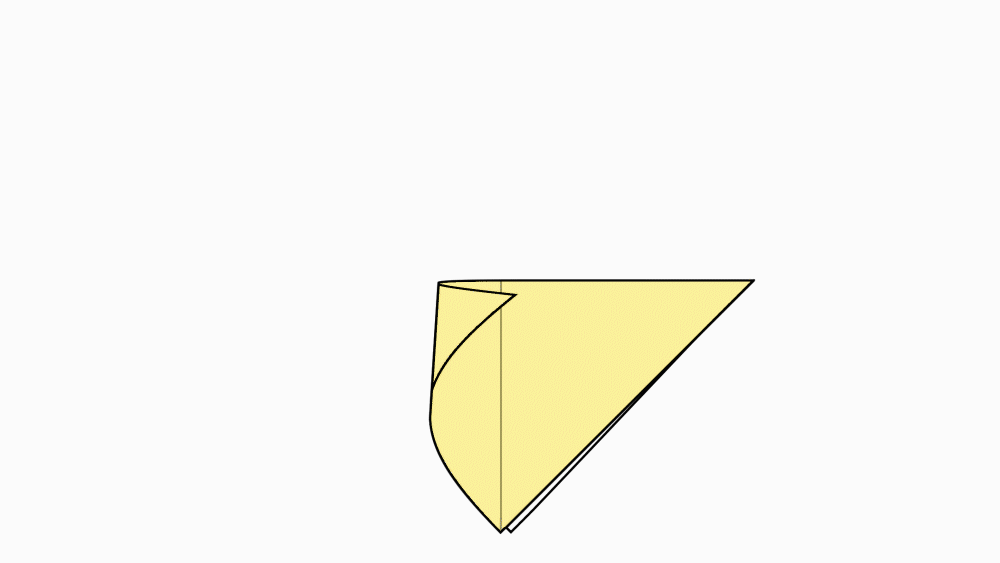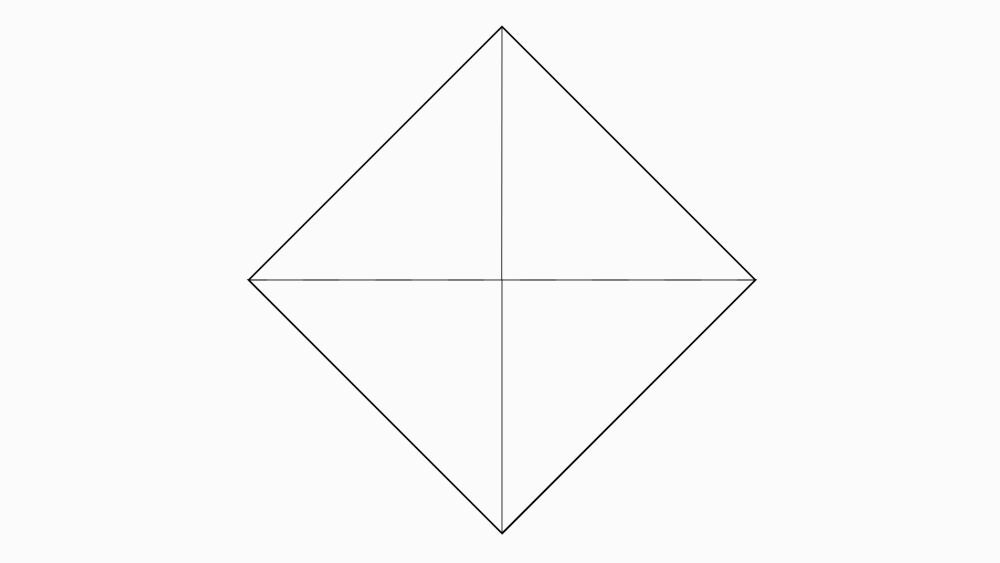
תשובה: כדי לקבל 4 משולשים חופפים, הצמדנו קדקוד אל הקדקוד הנגדי. בקיפול הנוסף הצמדנו שוב קדקוד לקדקוד ופתחנו בחזרה לריבוע.

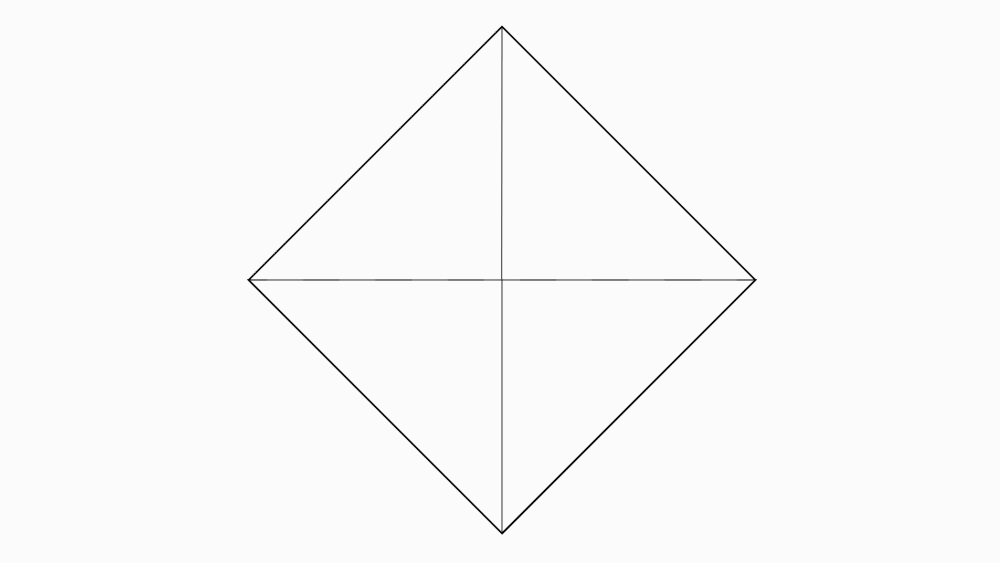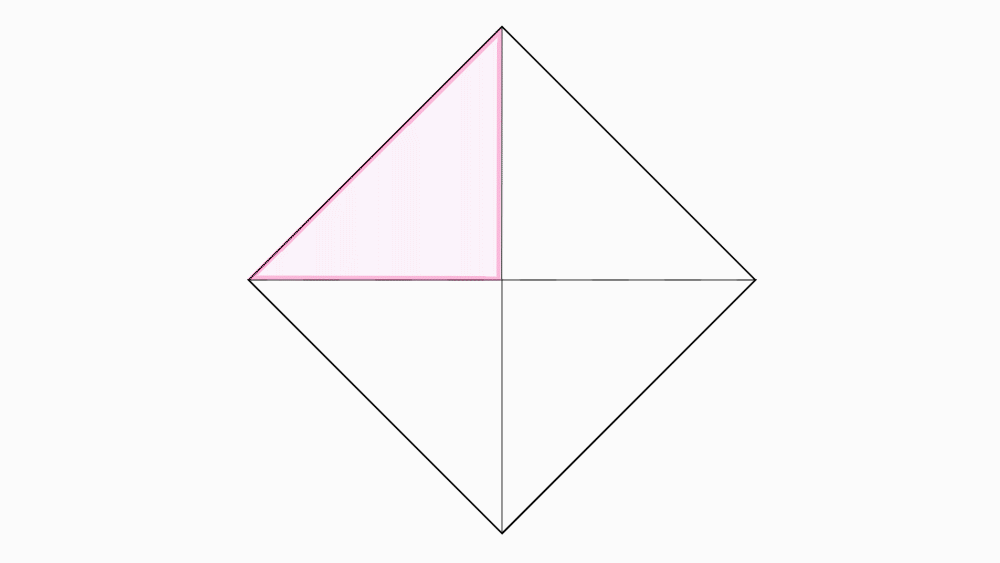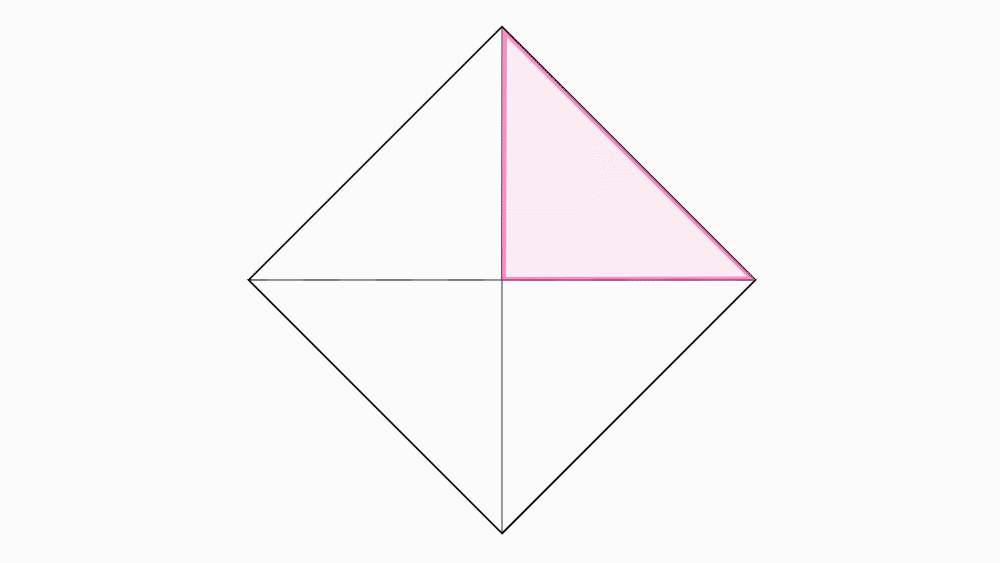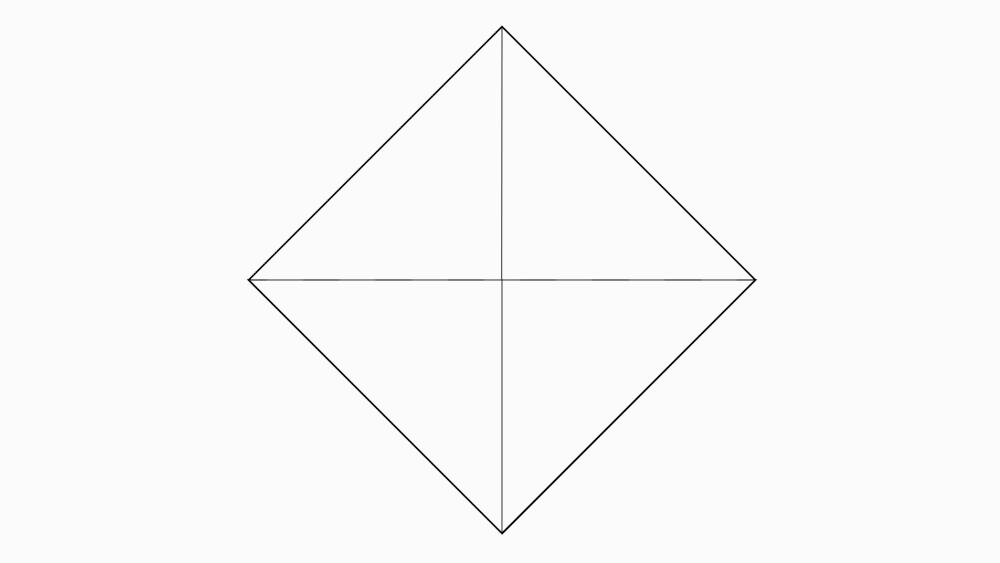
תשובה: שתי צורות הן חופפות כאשר אפשר לשים צורה אחת על האחרת, באופן שתכסה אותה בדיוק.

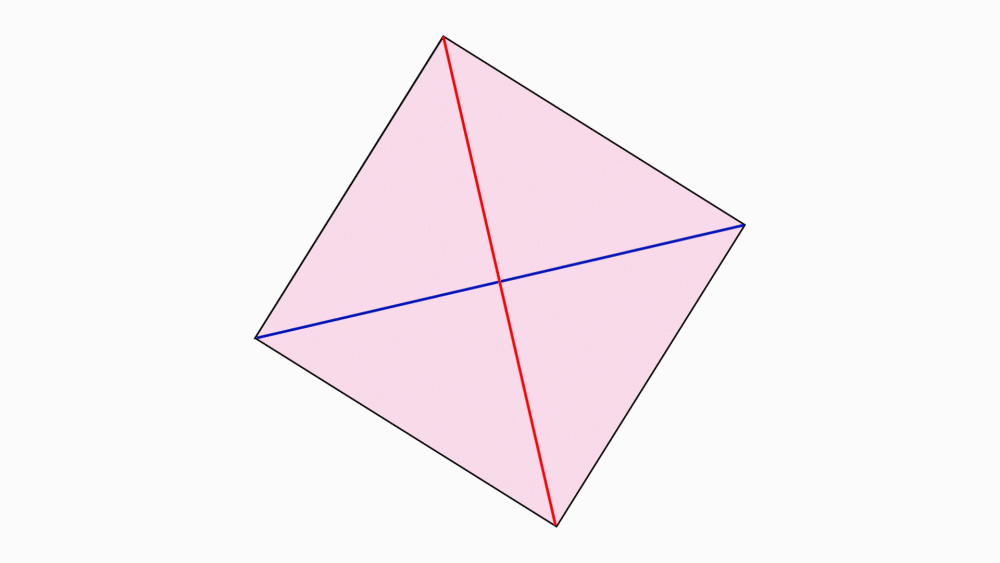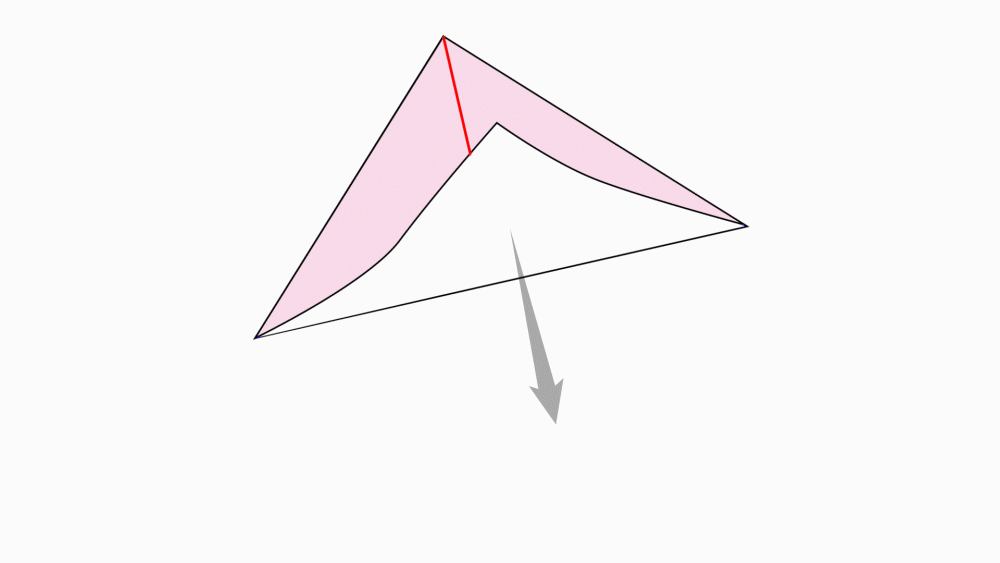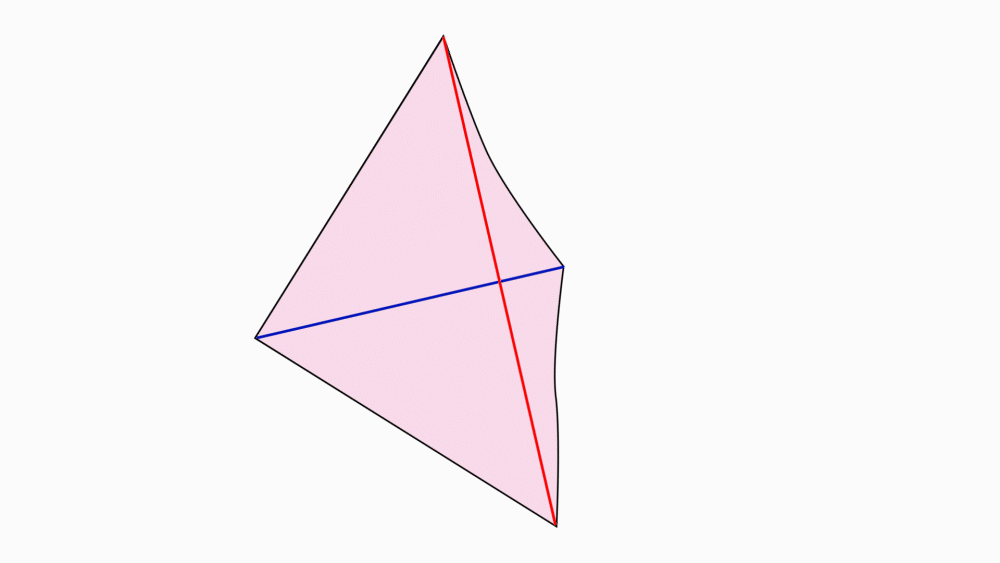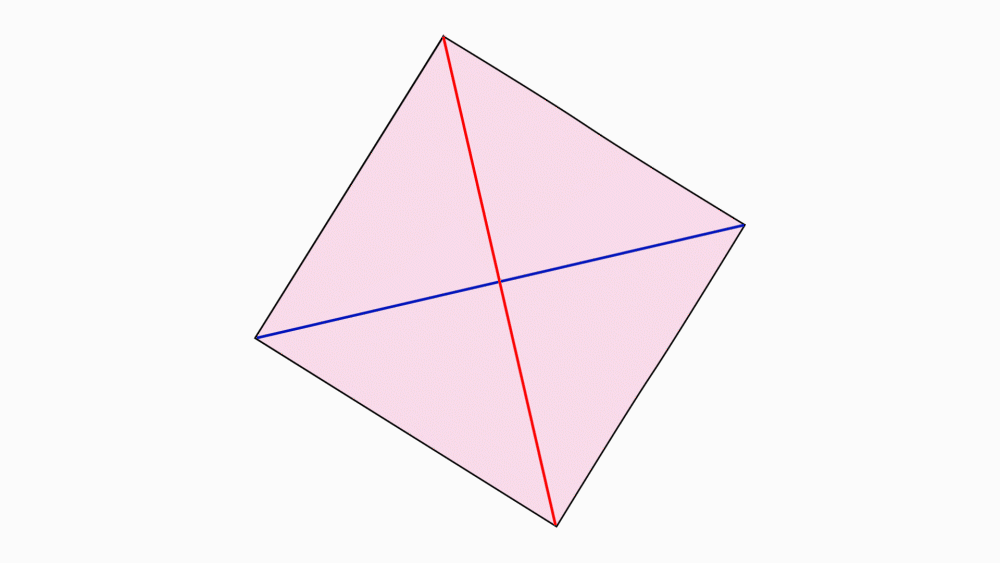
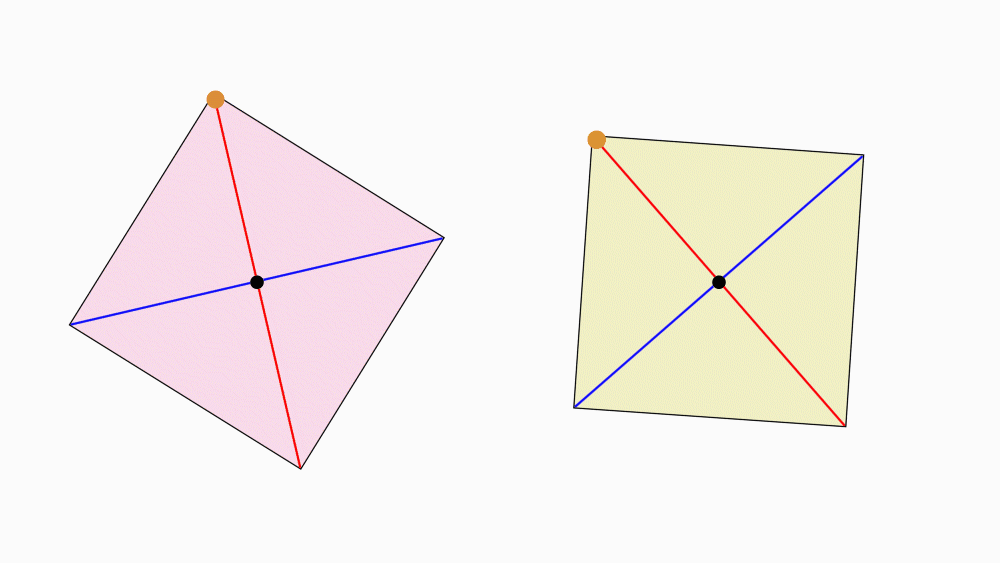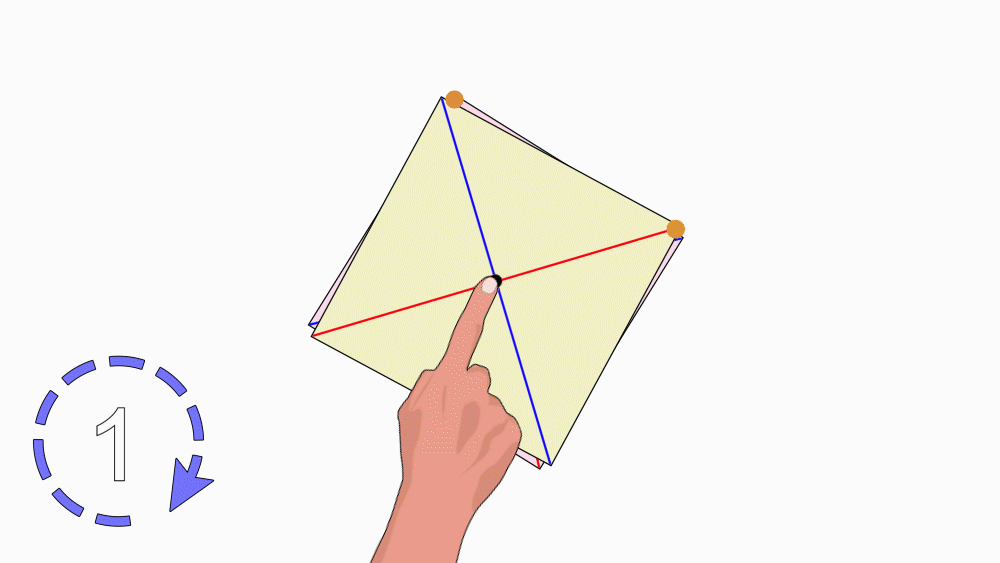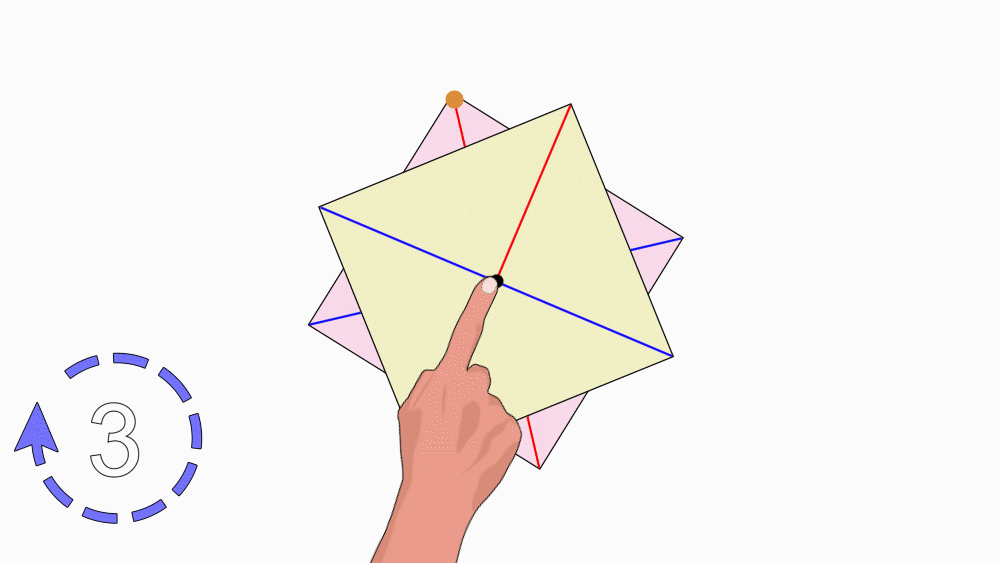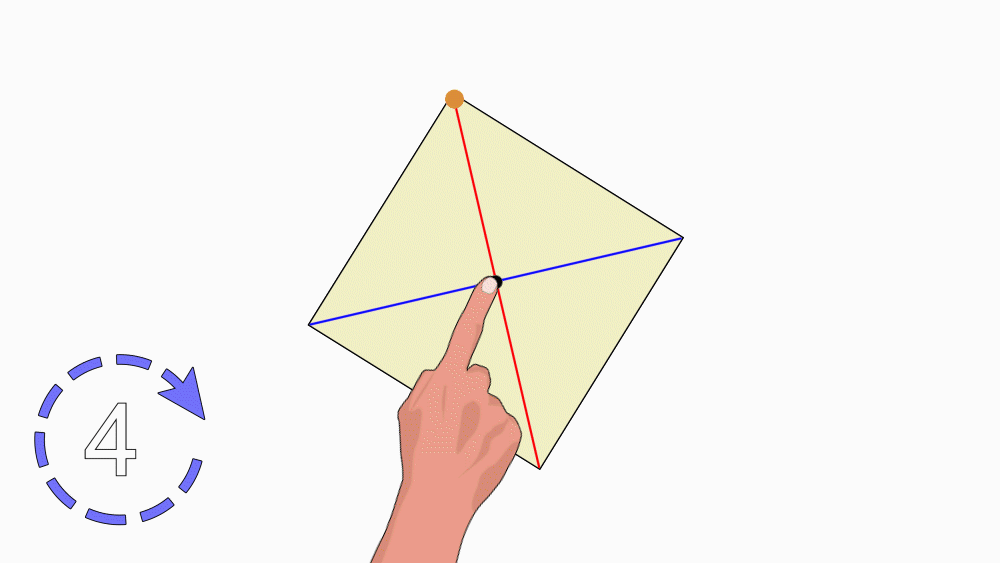
שאלה לדיון: מה ניתן לומר על שני הקטעים המחברים קדקודים נגדיים?

תשובה: שני הקטעים הם קווי הסימטריה של הריבוע וגם האלכסונים של הריבוע. בקיפול, צד אחד מכסה את הצד השני בדיוק.

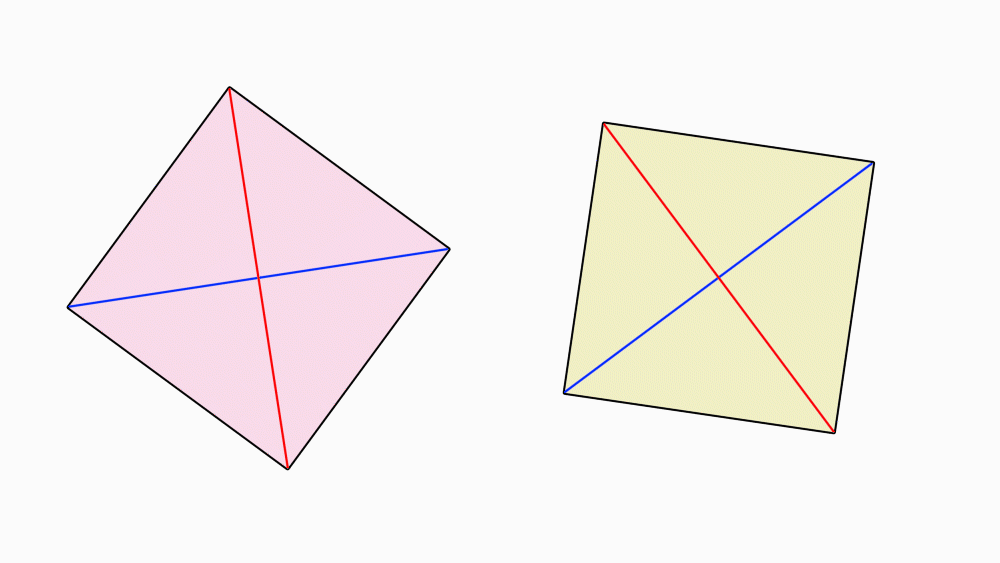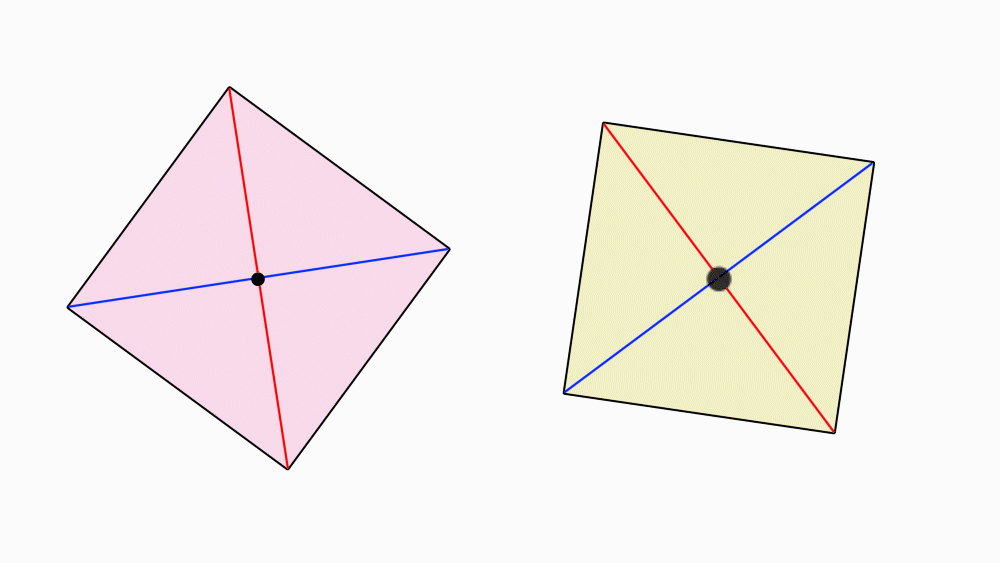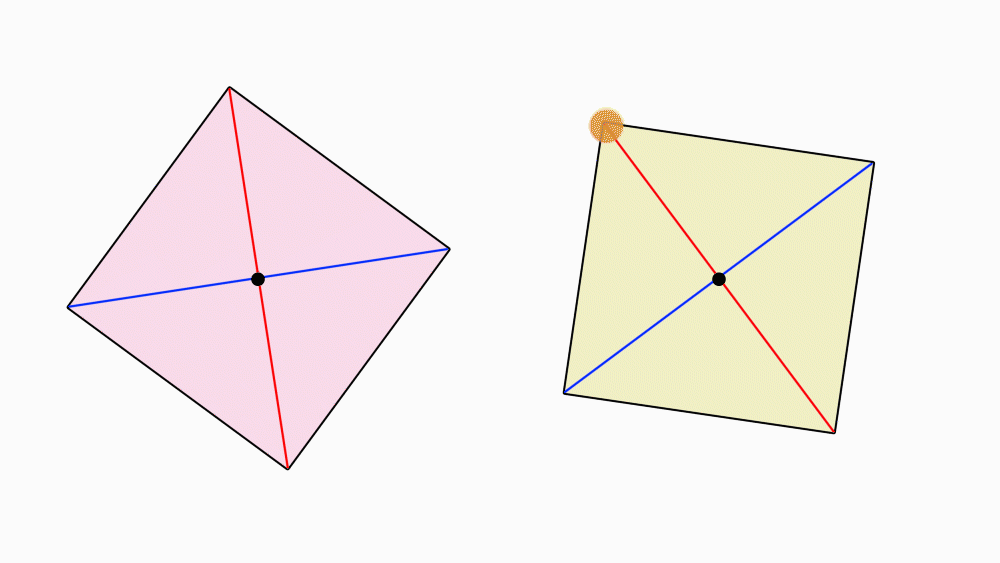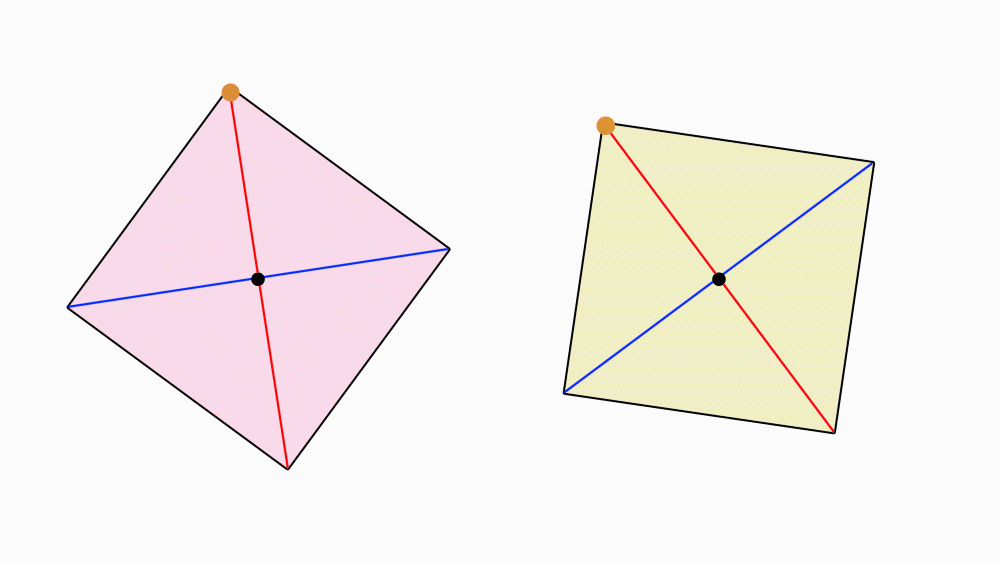
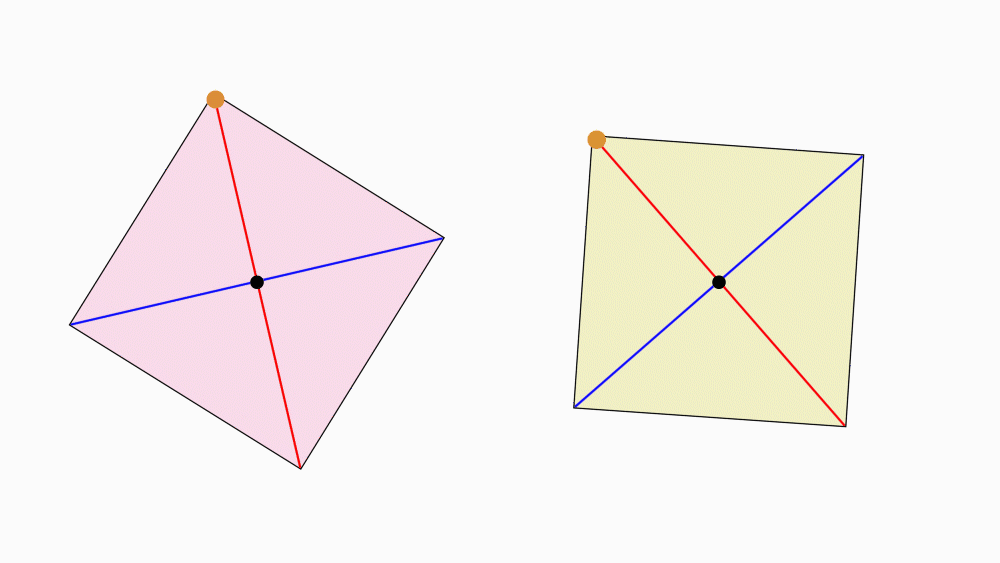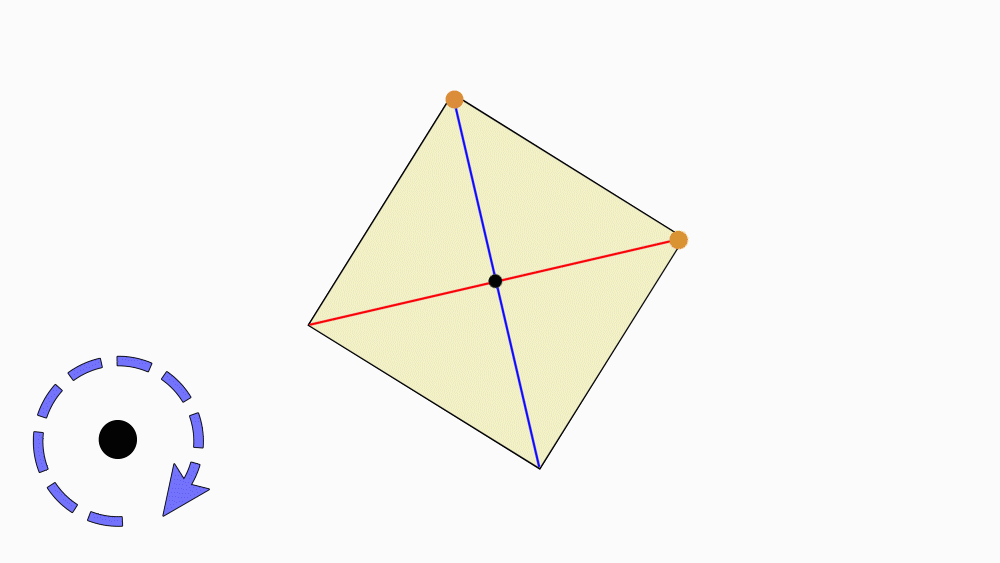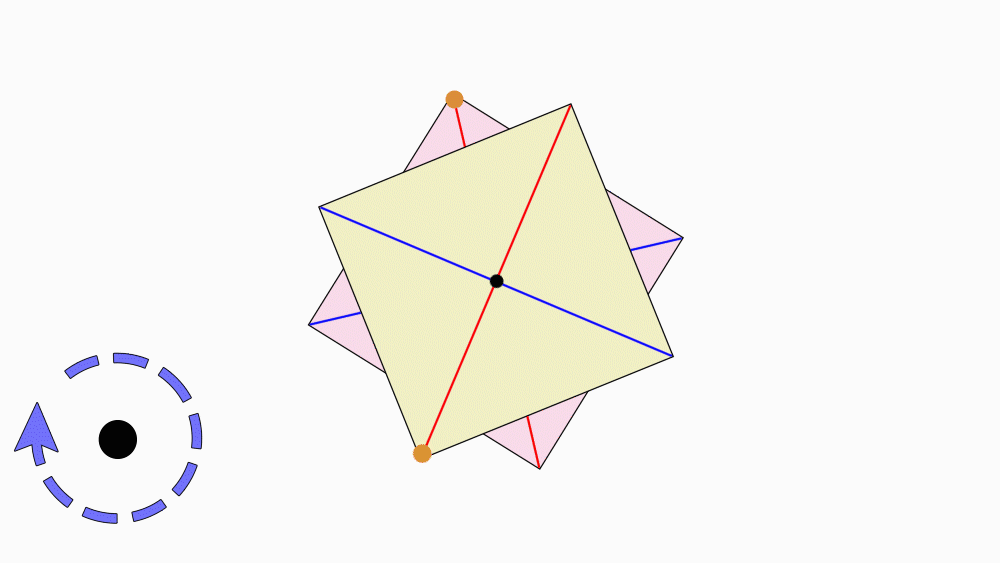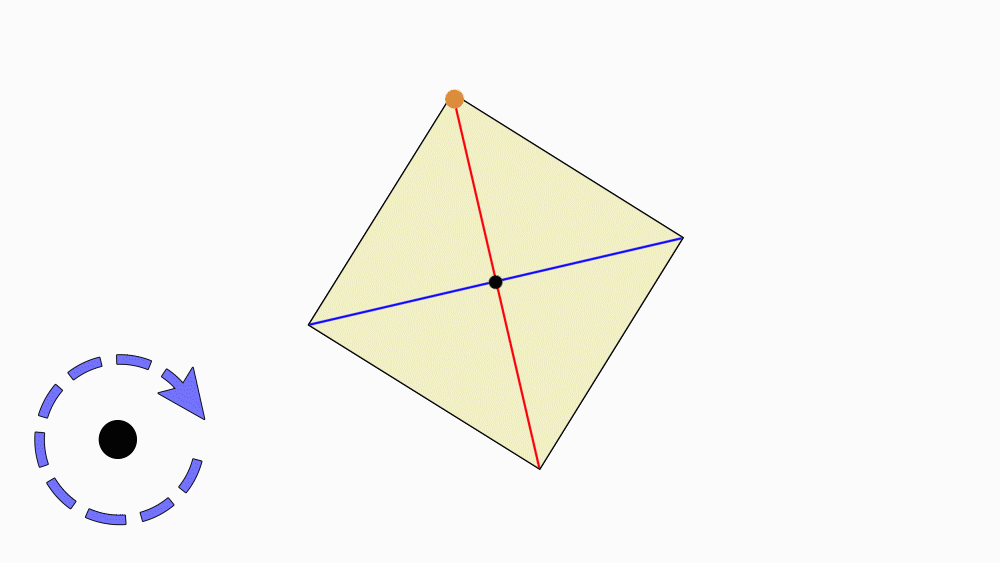
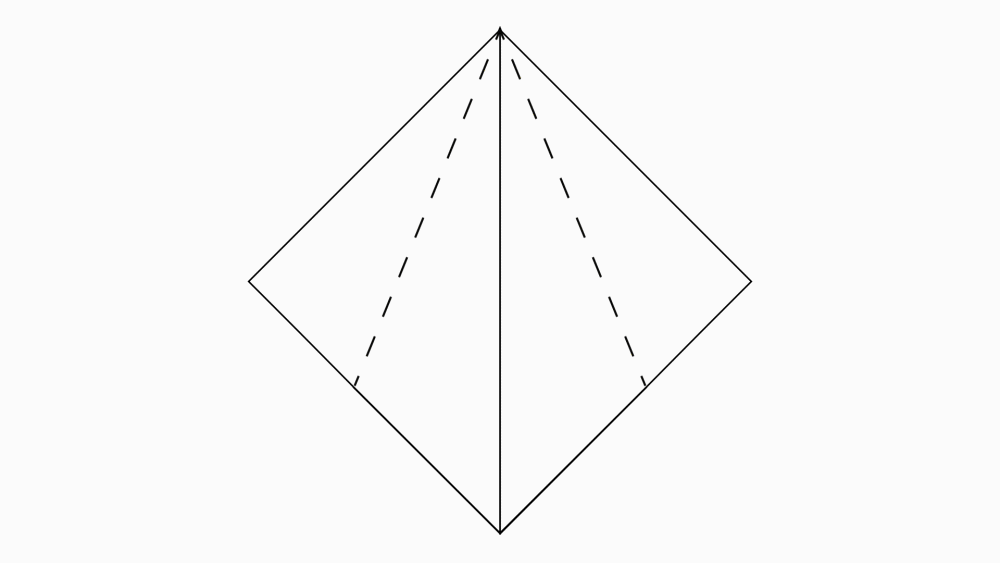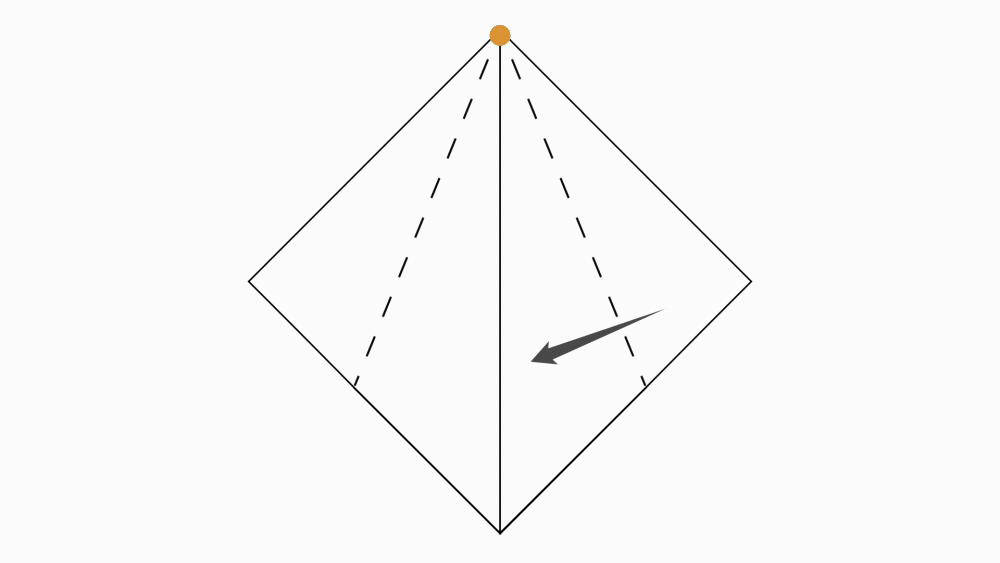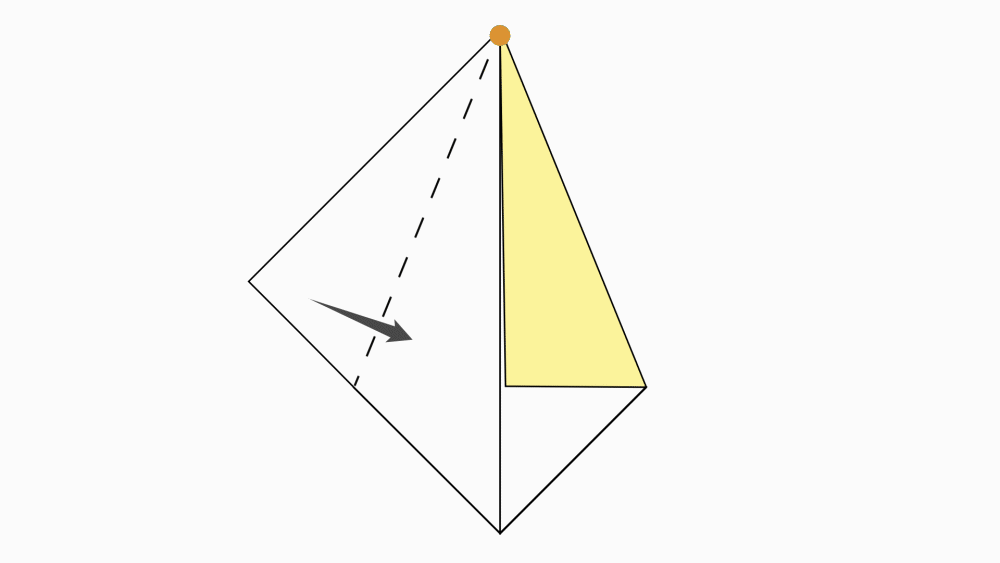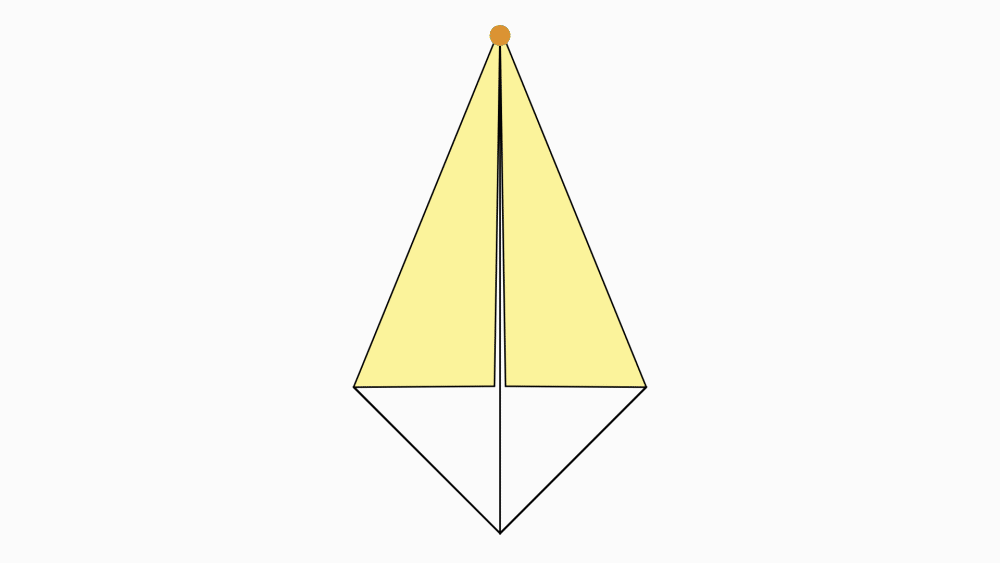
הנחיה: בכל אחד מהריבועים, סמנו את נקודת החיתוך של קווי הסימטריה השיקופית.

הניחו ריבוע על ריבוע ובחרו קדקוד משותף. סמנו את שני הקדקודים המשותפים.

יש לסמן את הנקודות בצד הצבעוני וגם בצד הלבן של הנייר.

הנחיה: הניחו את שני הריבועים האחד מעל השני, כך שהנקודות שסימנתם יהיו האחת על גבי השנייה. הציבו כלי כתיבה או אצבע בנקודת מפגש קווי הסימטריה וסובבו את הנייר העליון.

שאלה לדיון: בחנו כמה פעמים ריבוע אחד כיסה את הריבוע השני במהלך סיבוב שלם, נמקו.

תשובה: לריבוע יש דרגת סיבוב 4. במהלך סיבוב שלם, ריבוע אחד כיסה את הריבוע השני ארבע פעמים. ולכן, לריבוע יש סימטריה סיבובית.

הוראת קיפול: לקפל כל צלע הסמוכה לקדקוד המסומן אל קו הסימטריה. יש לקפל בשני הריבועים.

(שימו לב: לקפל מהקדקוד המסומן בנקודה.)

הוראת קיפול: לקפל את המשולש הלבן ולפתוח.

הוראת קיפול: להפוך את הנייר לצד השני.

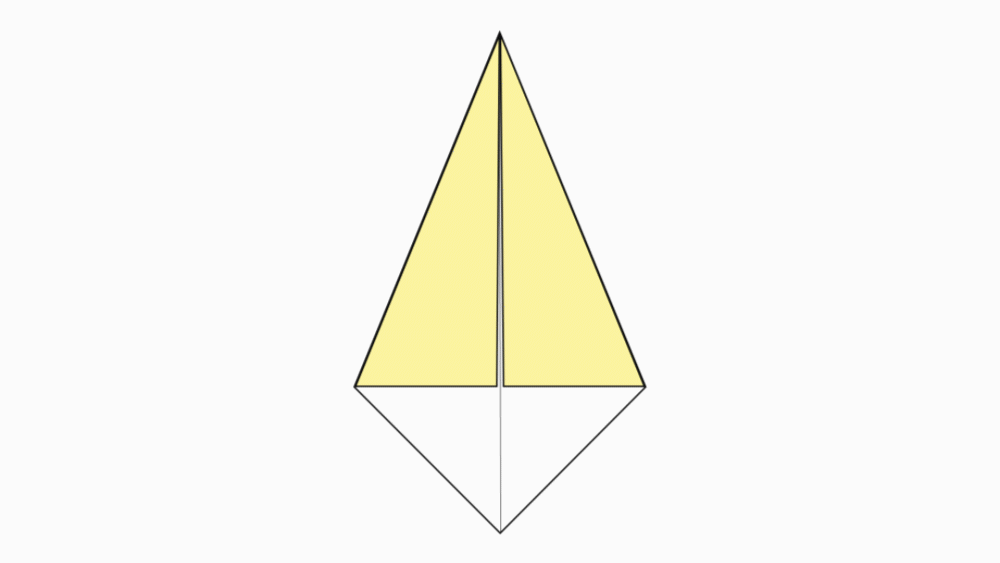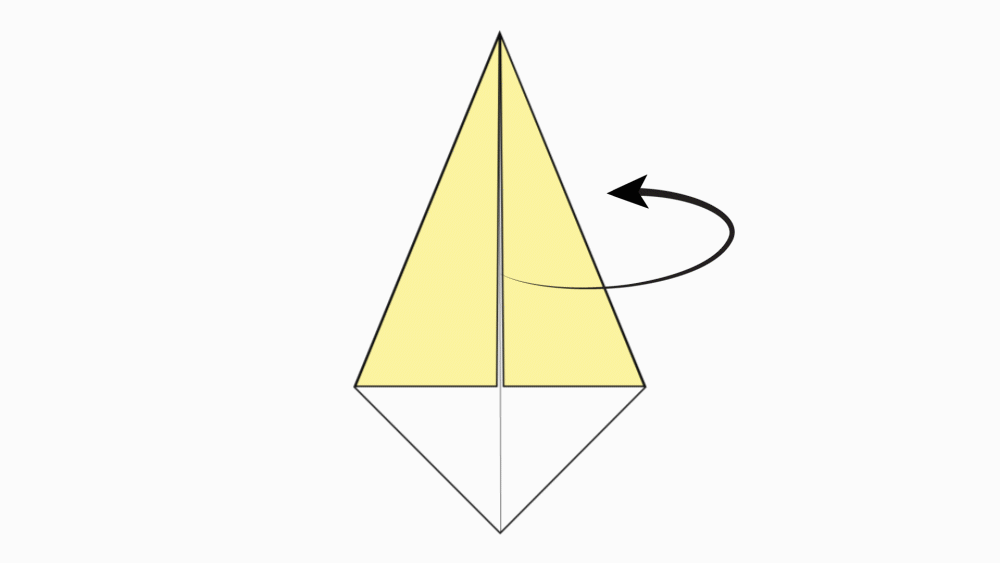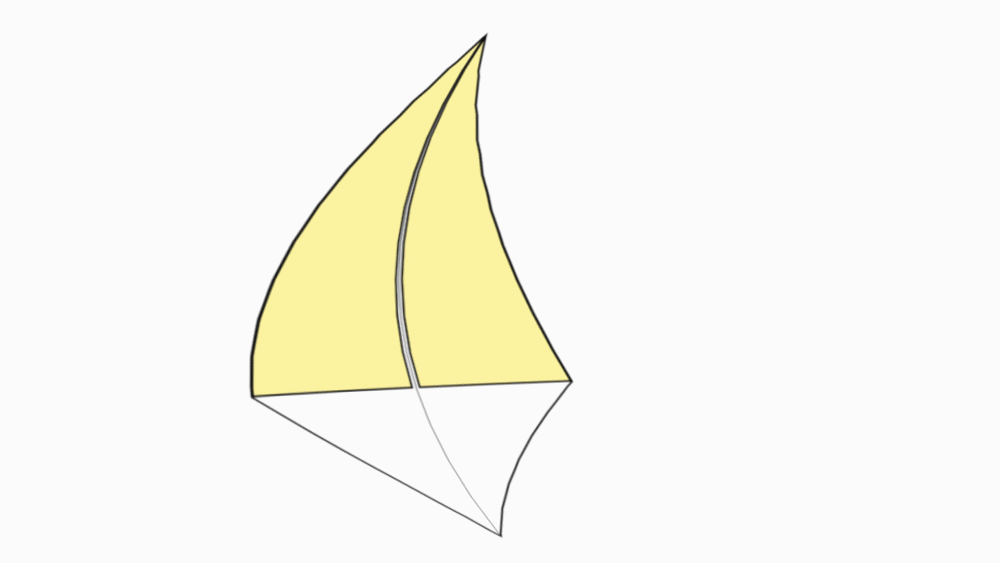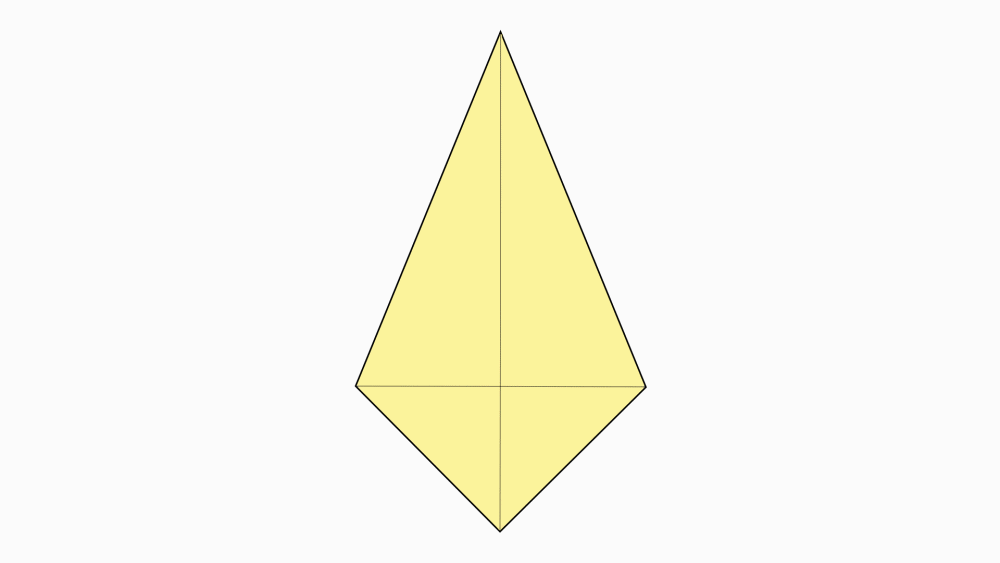
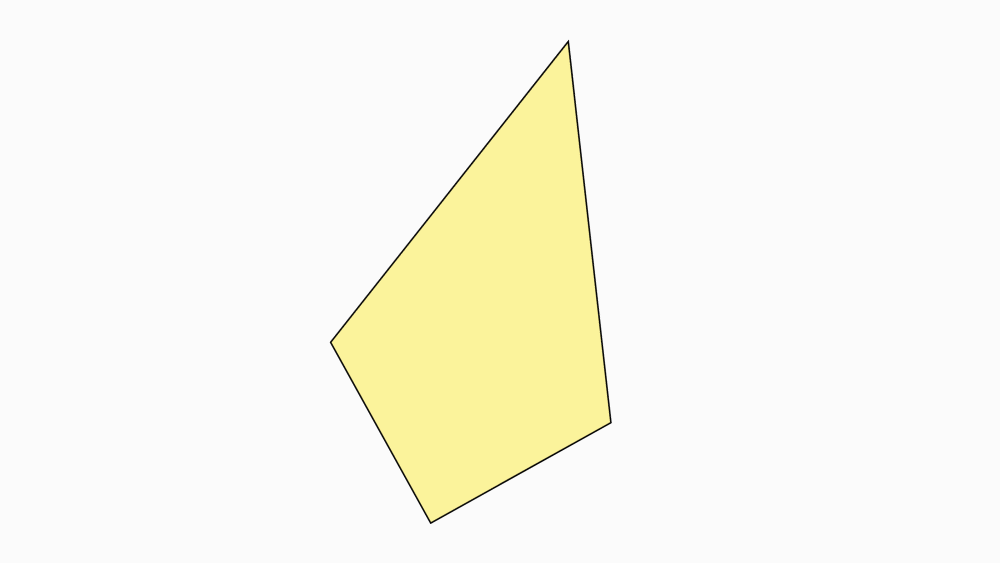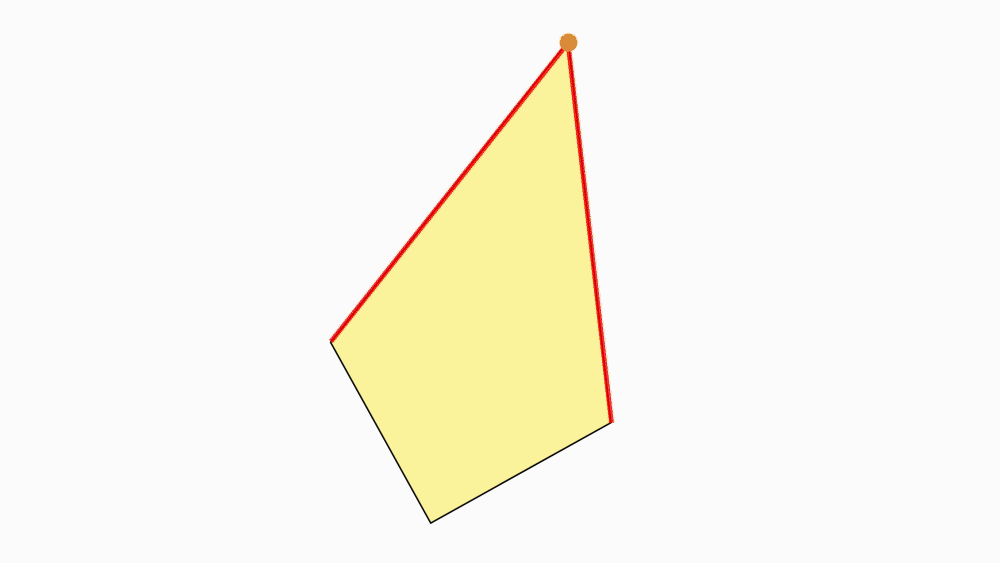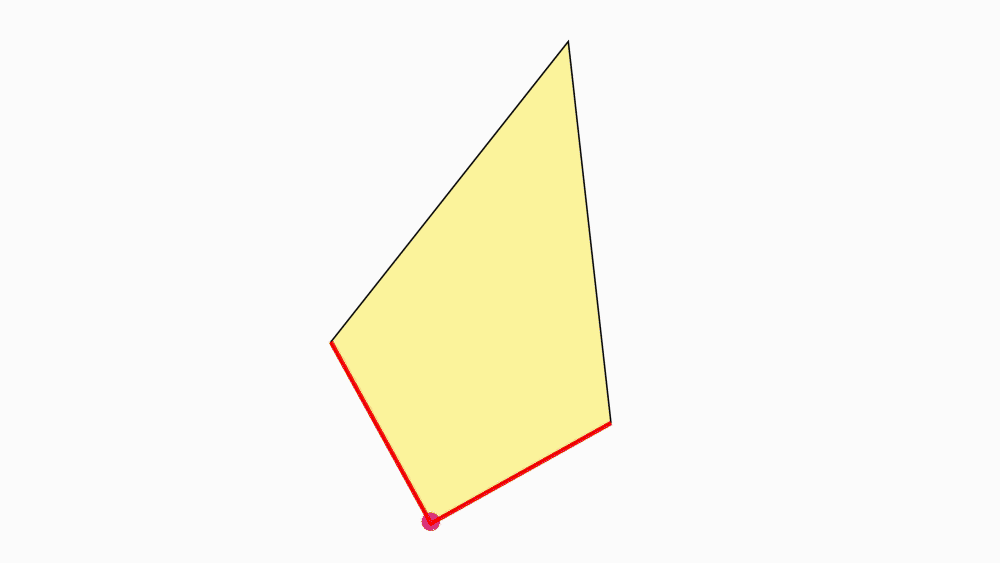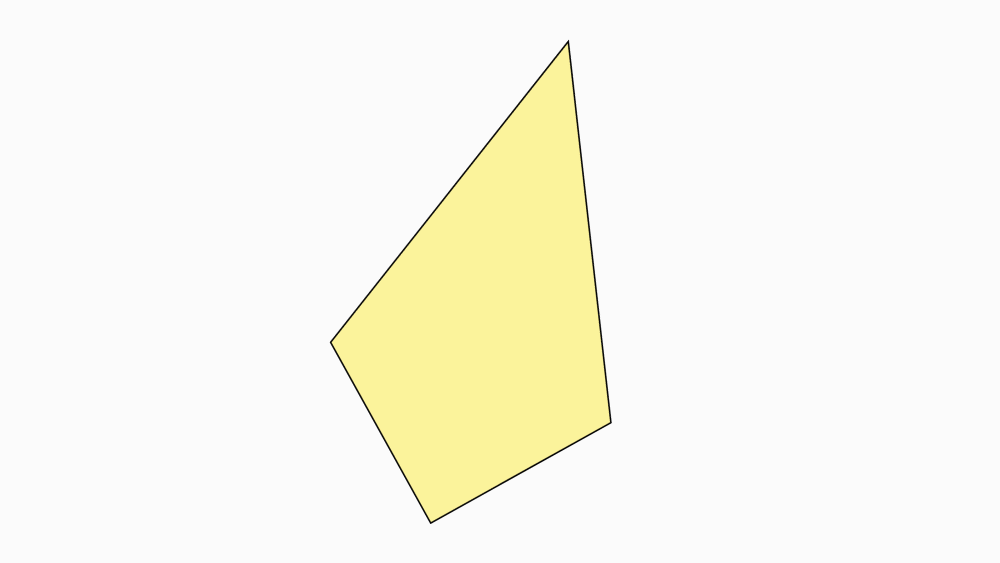
שאלה לדיון: האם נוכל לתת שם מיוחד (או נוסף) למרובע זה?

תשובה: המרובע הוא דלתון, לדלתון שני זוגות נפרדים של צלעות סמוכות שוות באורכן.

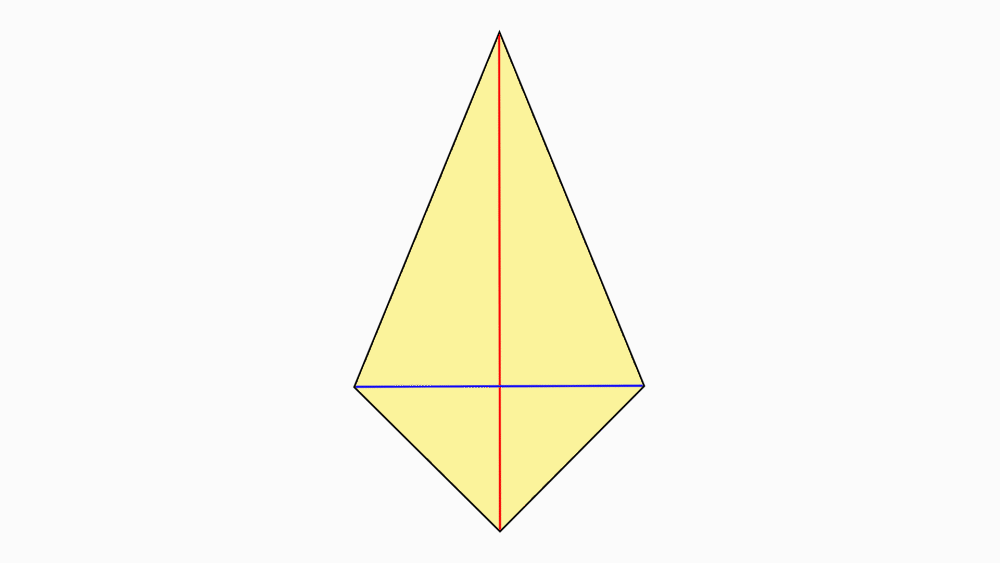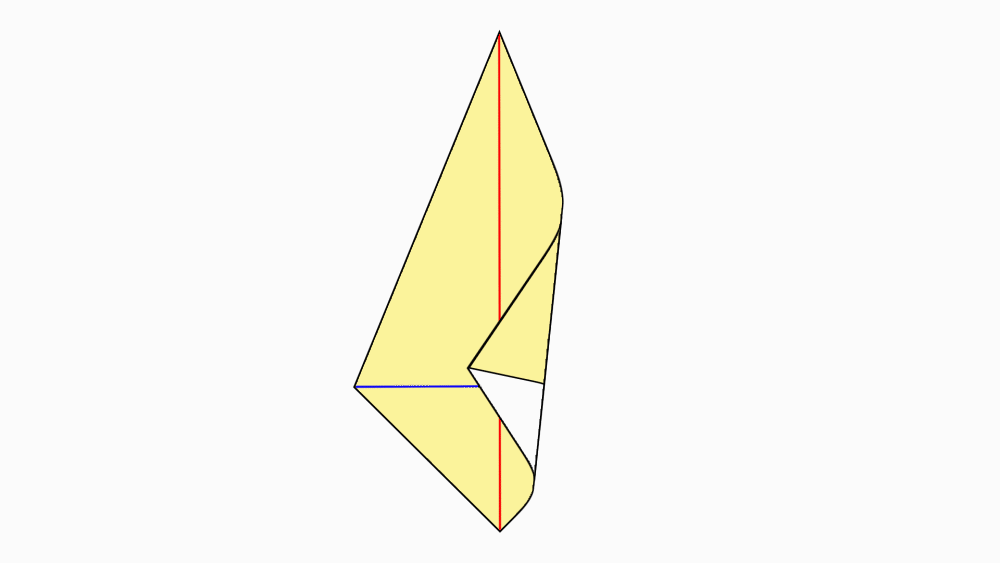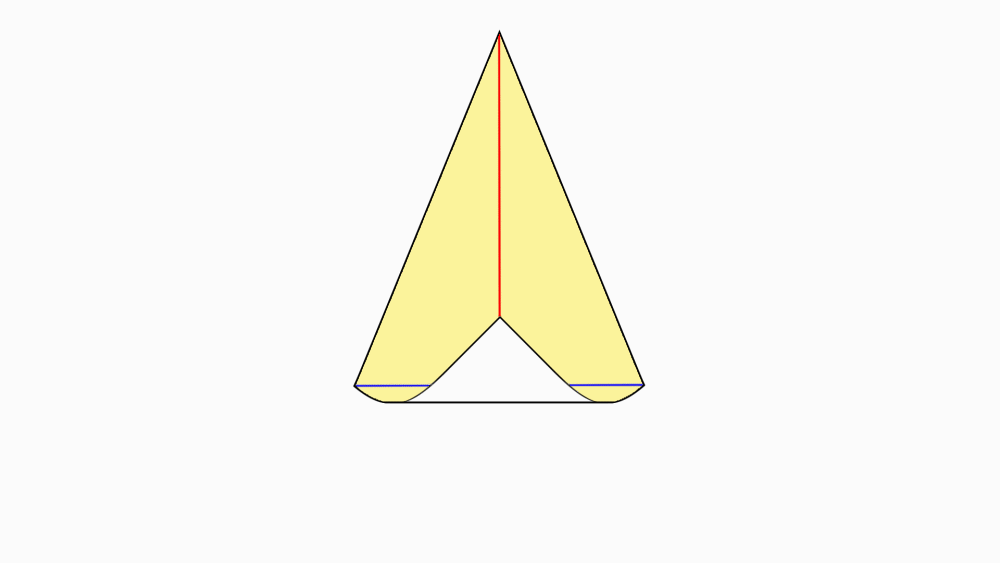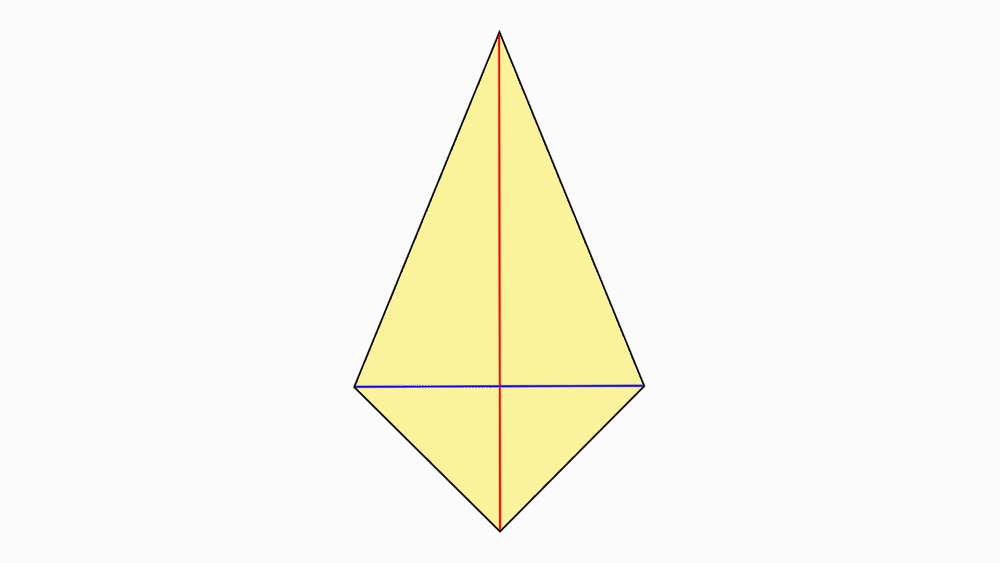
שאלה לדיון: האם האלכסונים של הדלתון הם קווי הסימטריה של הדלתון? נמקו.

תשובה: אחד האלכסונים הוא קו הסימטריה של הדלתון, מכיוון שבקיפול משולש אחד מכסה את המשולש השני בדיוק.

הישר השני אינו קו הסימטריה מכיוון שבקיפול משולש אחד אינו מכסה בדיוק את המשולש השני.

הוראת קיפול: לסמן את נקודת החיתוך של האלכסונים בשני הדלתונים.

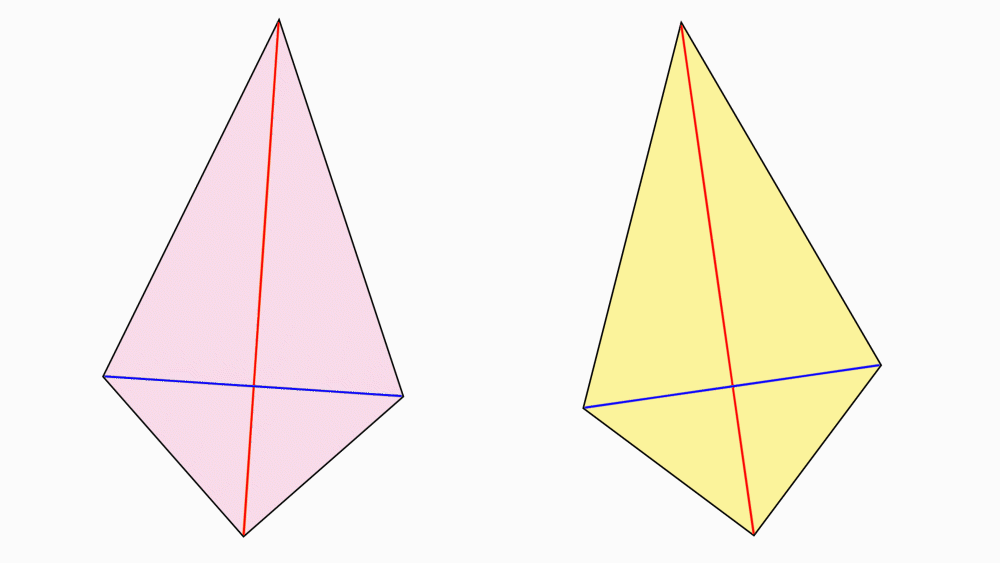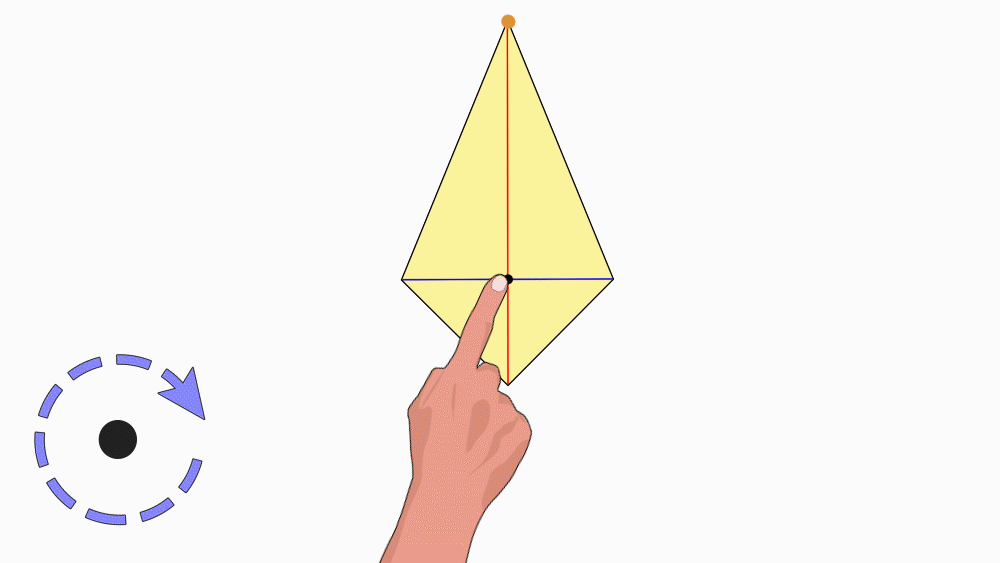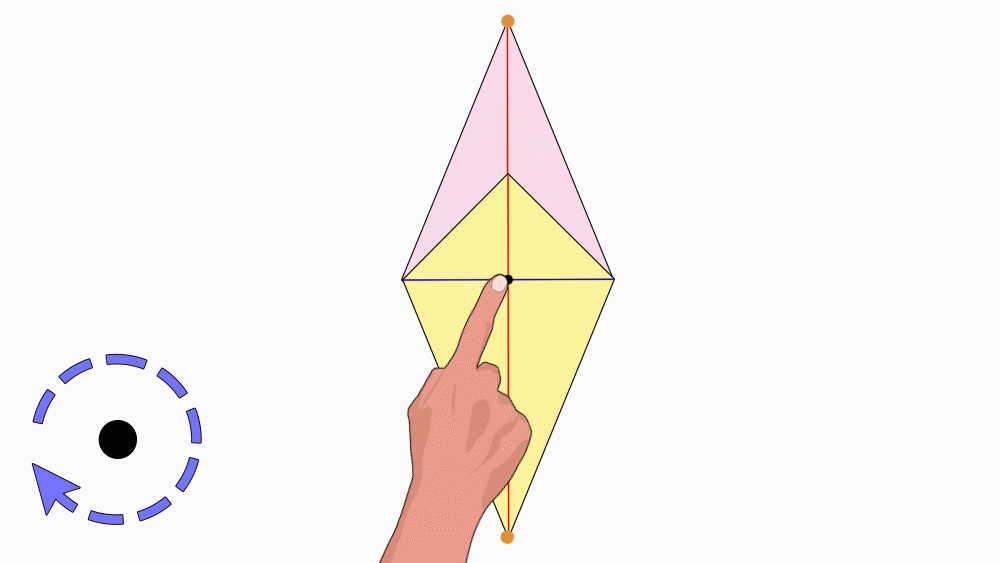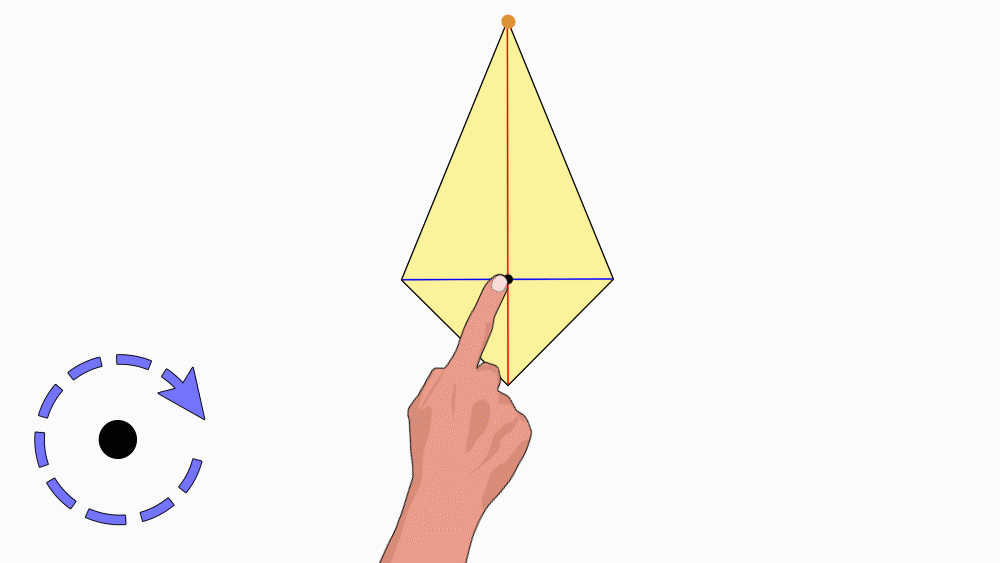
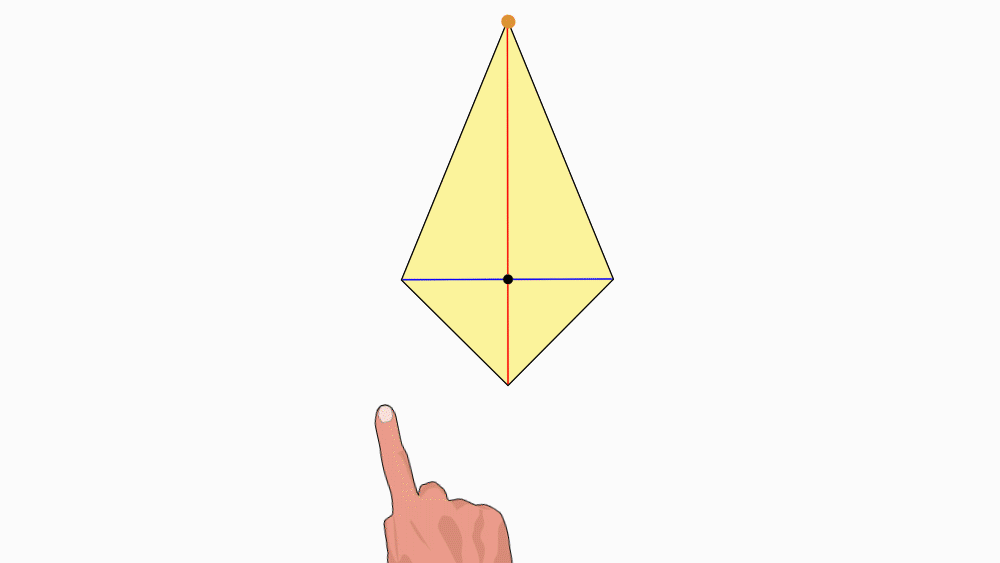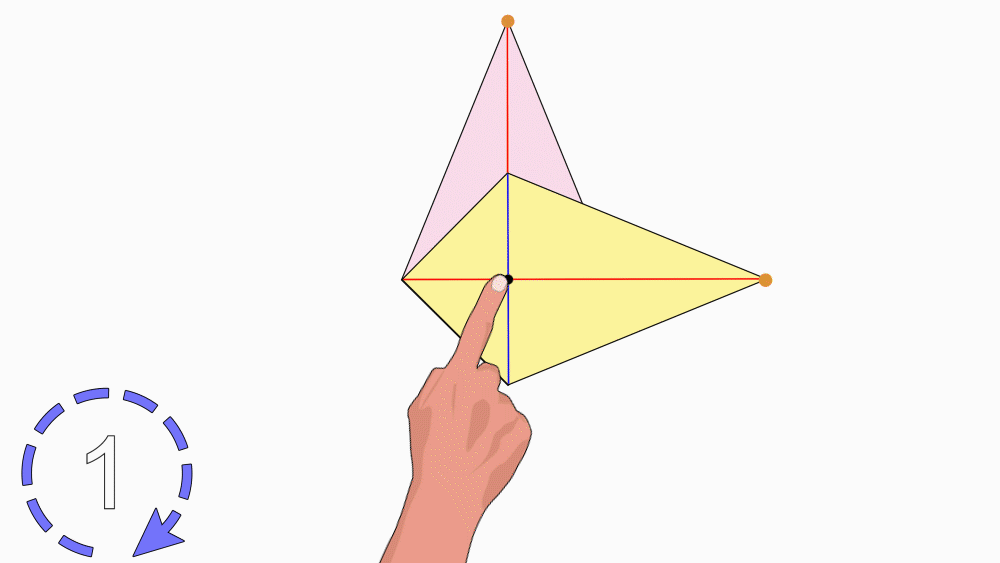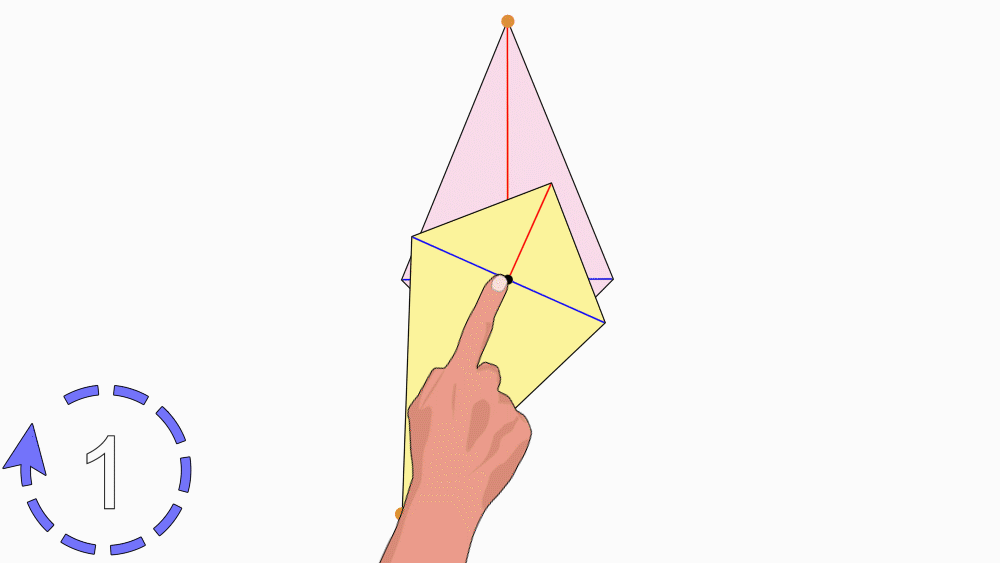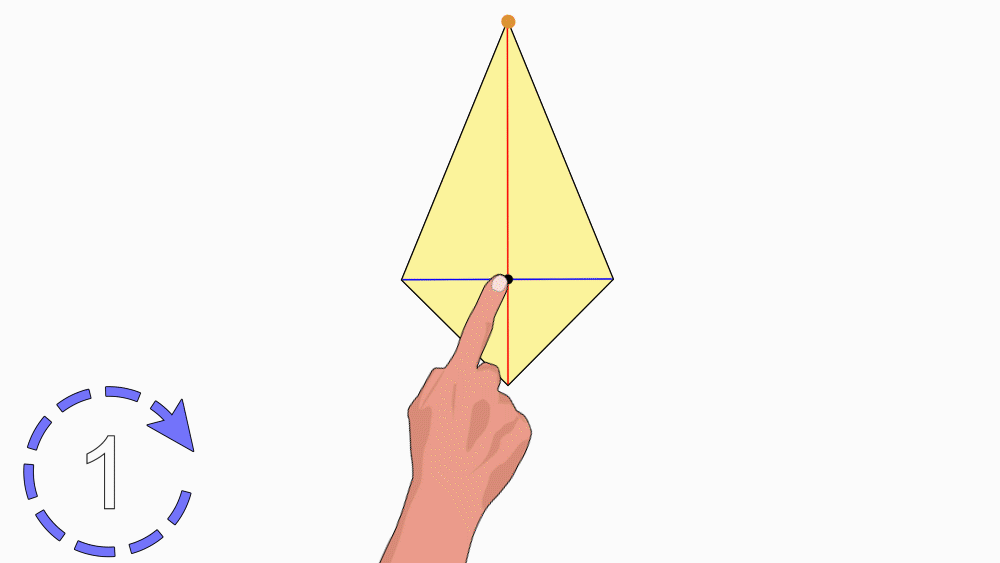
הנחיה: הניחו את שני הדלתונים האחד מעל השני כך שהנקודות יהיו האחת על גבי השנייה. הציבו כלי כתיבה או אצבע בנקודת החיתוך של קווי הסימטריה וסובבו את הנייר העליון.

שאלה לדיון: בחנו כמה פעמים דלתון אחד כיסה את הדלתון השני במהלך סיבוב שלם? נמקו.

תשובה: לדלתון יש דרגת סיבוב 1. במהלך סיבוב שלם, דלתון אחד כיסה את הדלתון השני פעם אחת בלבד.

כאשר צורה אחת מכסה צורה שנייה פעם אחת, לצורה אין סימטריה סיבובית.

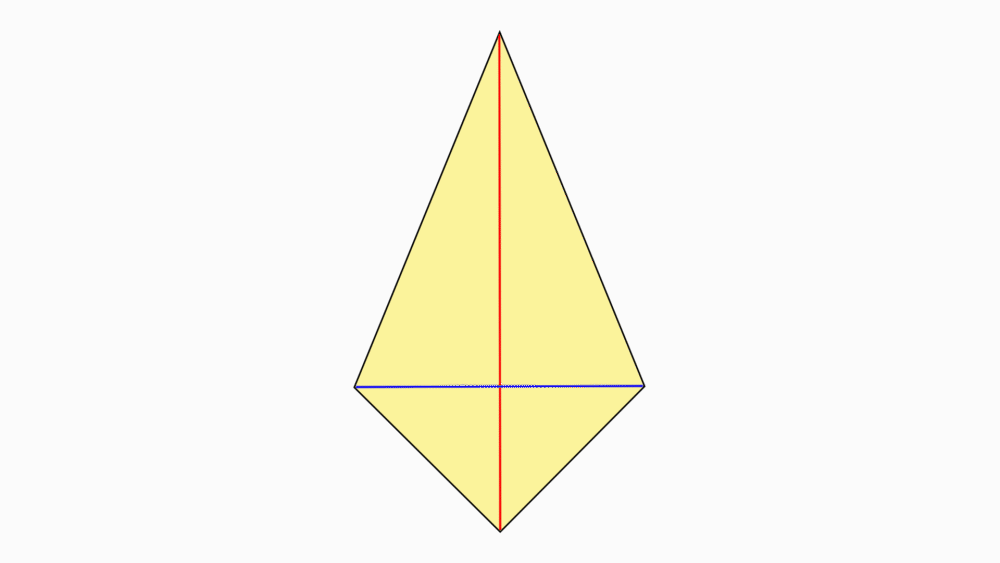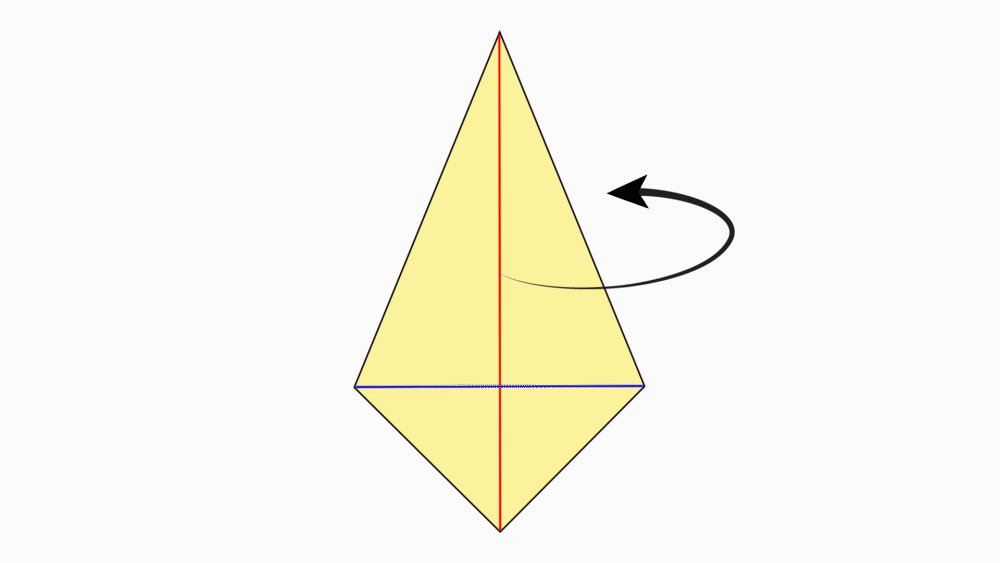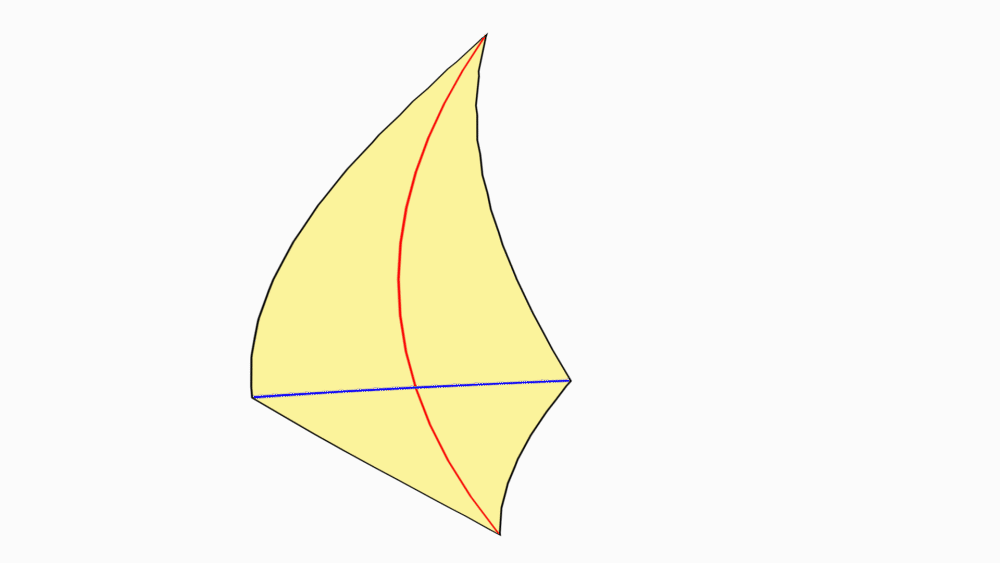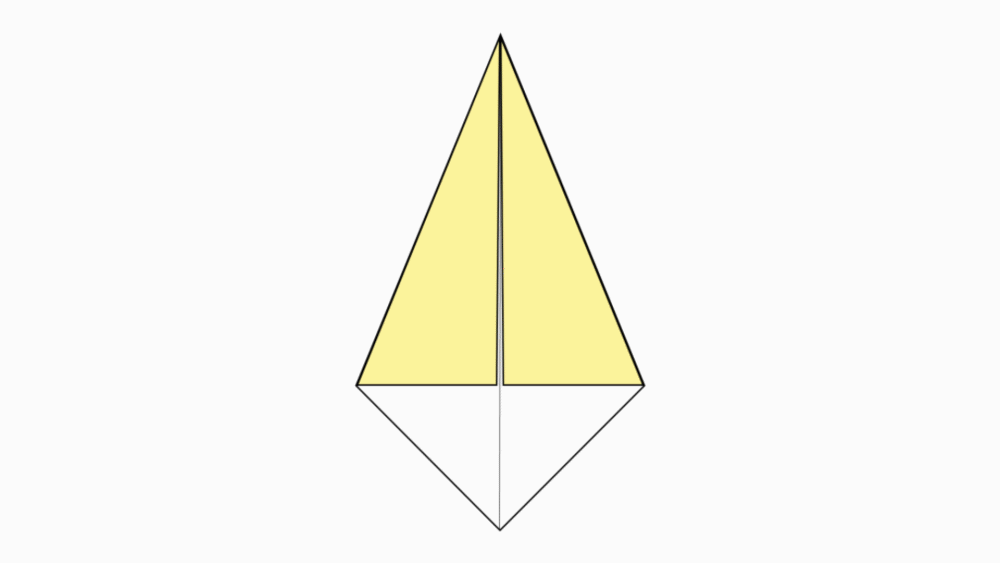
הוראת קיפול: להפוך את שני הניירות לצד השני.

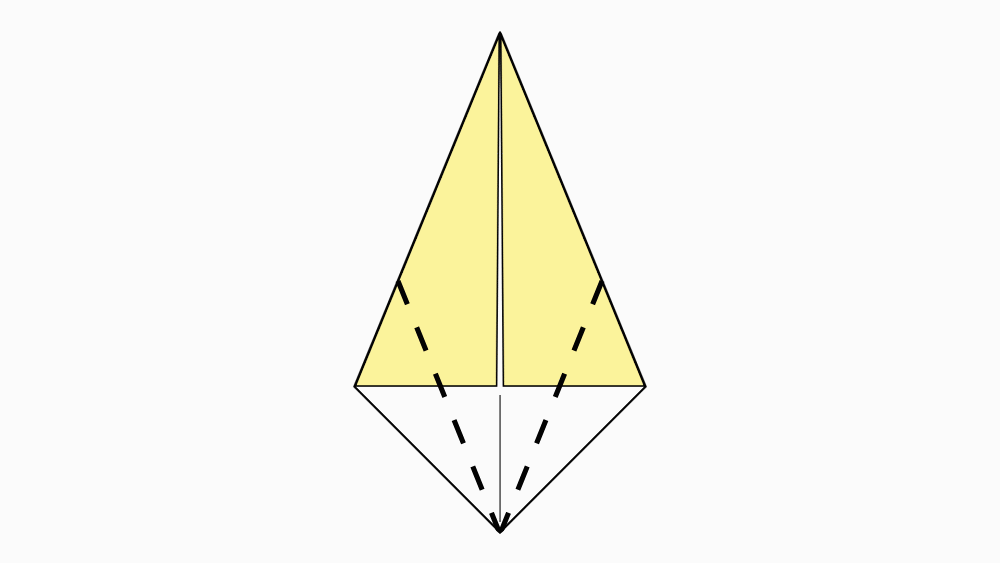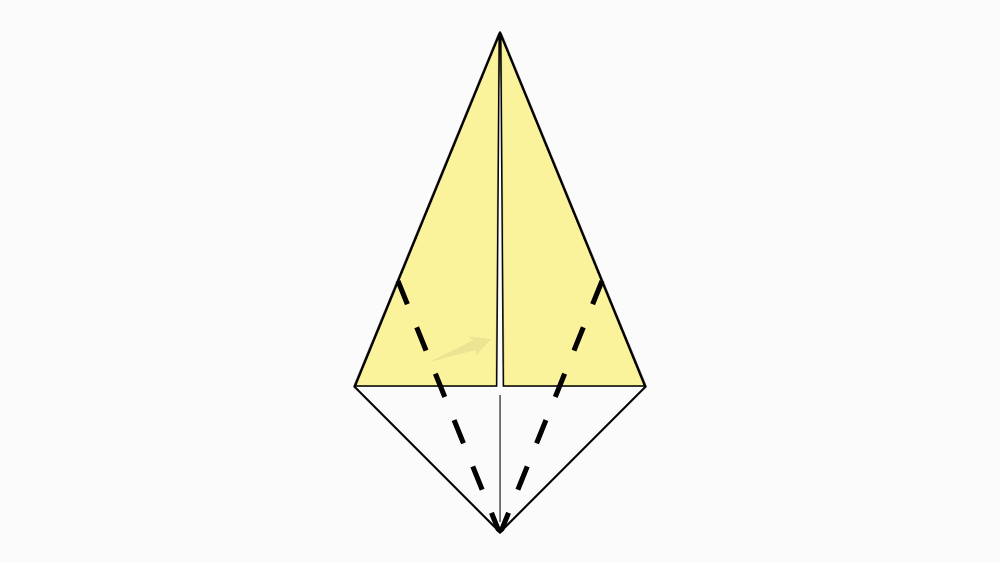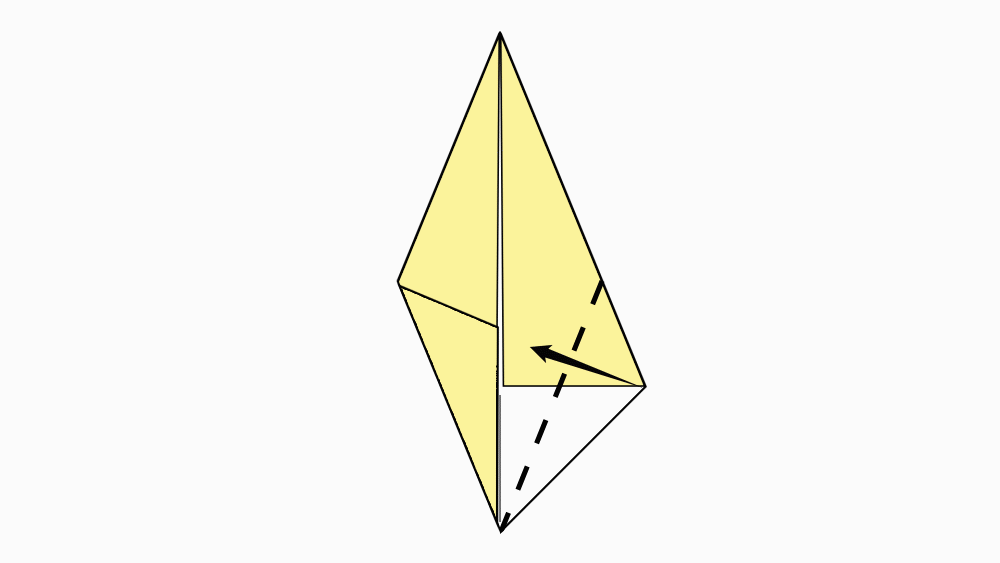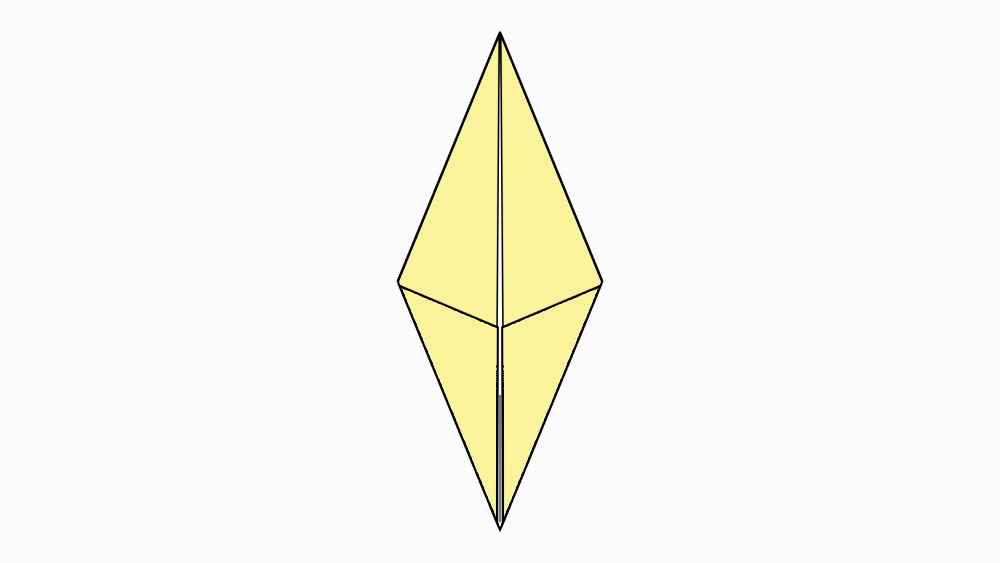
הוראת קיפול: לקפל כל צלע קצרה של הדלתון אל קו הסימטריה, לפי הסימון.

הוראת קיפול: להפוך את הניירות לצד השני.

שאלה לדיון: מה ניתן לומר על הצורה שהתקבלה? נמקו.

תשובה: קיבלנו מעוין. מרובע שכל צלעותיו שוות זו לזו הוא מעוין.

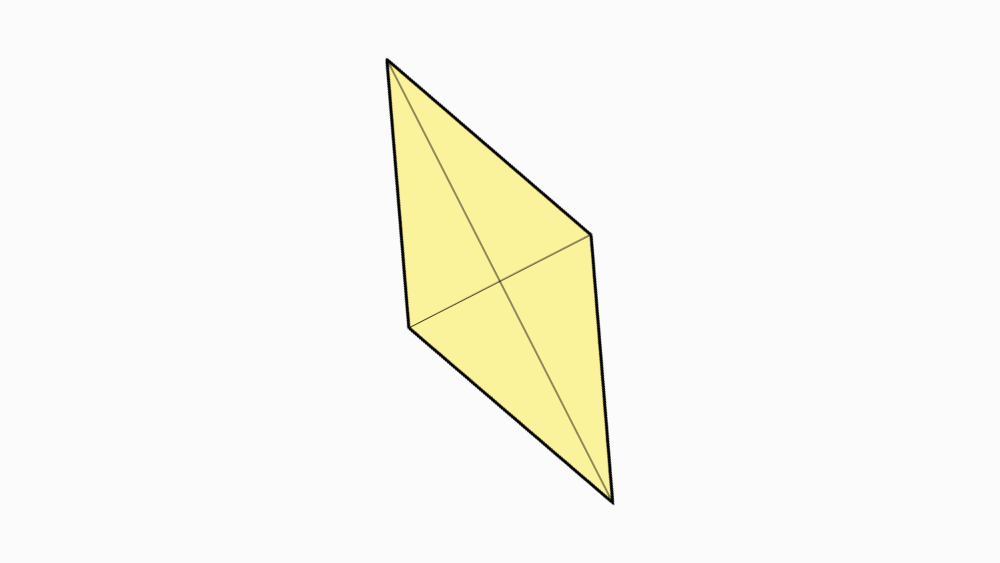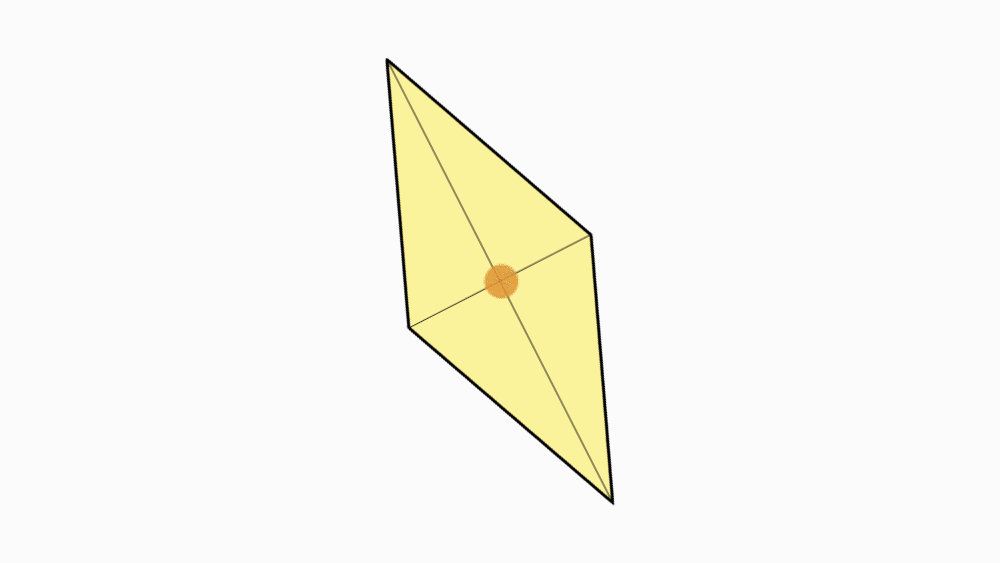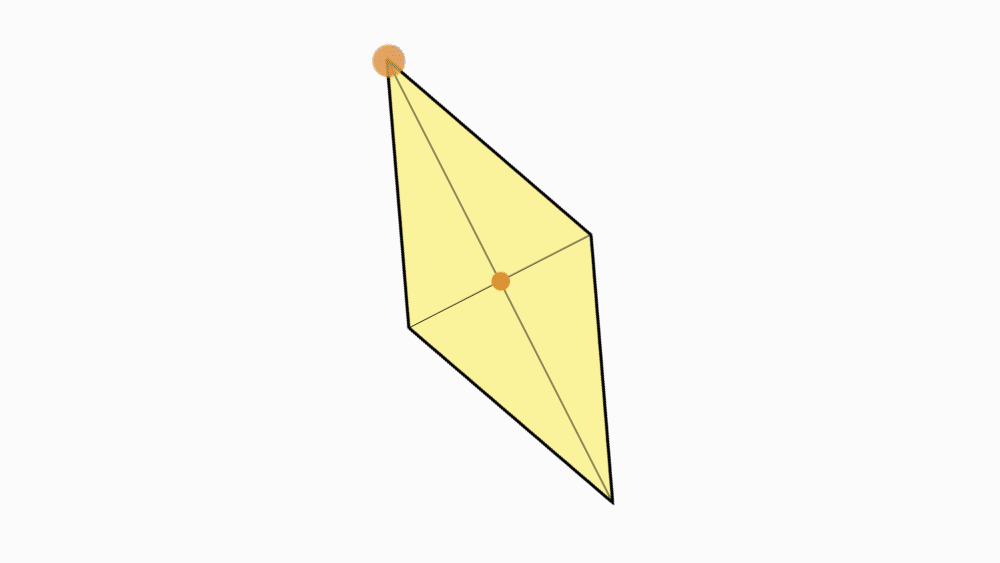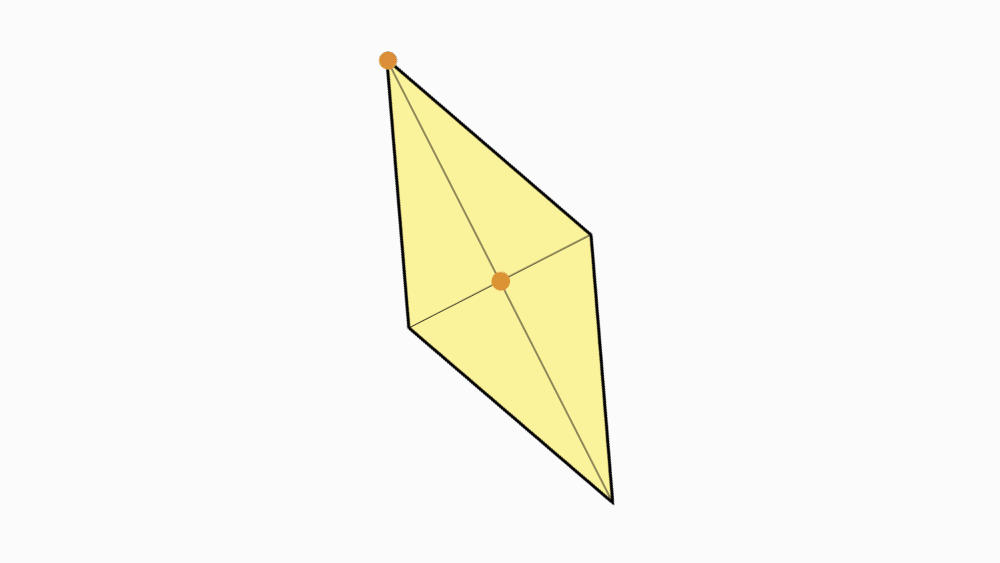
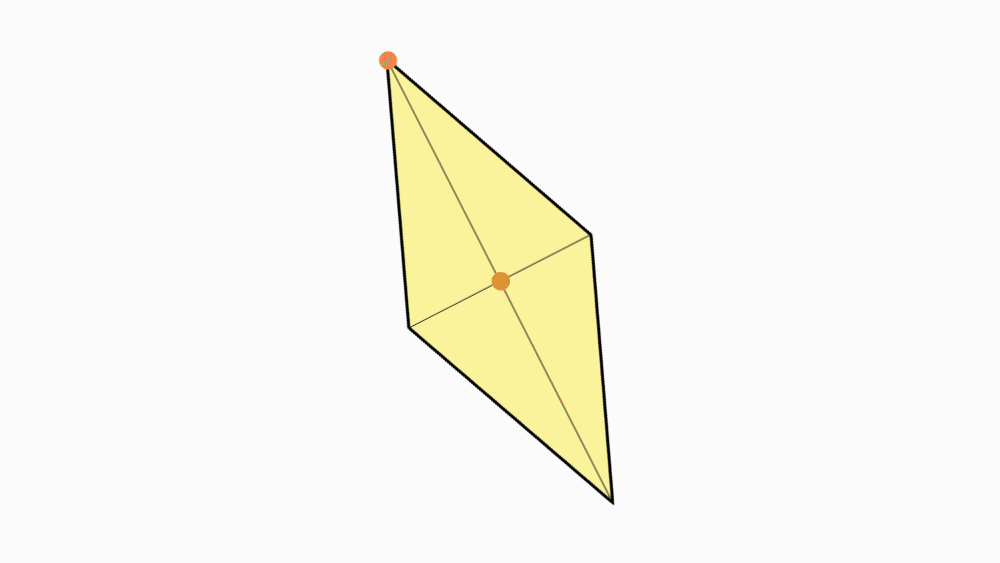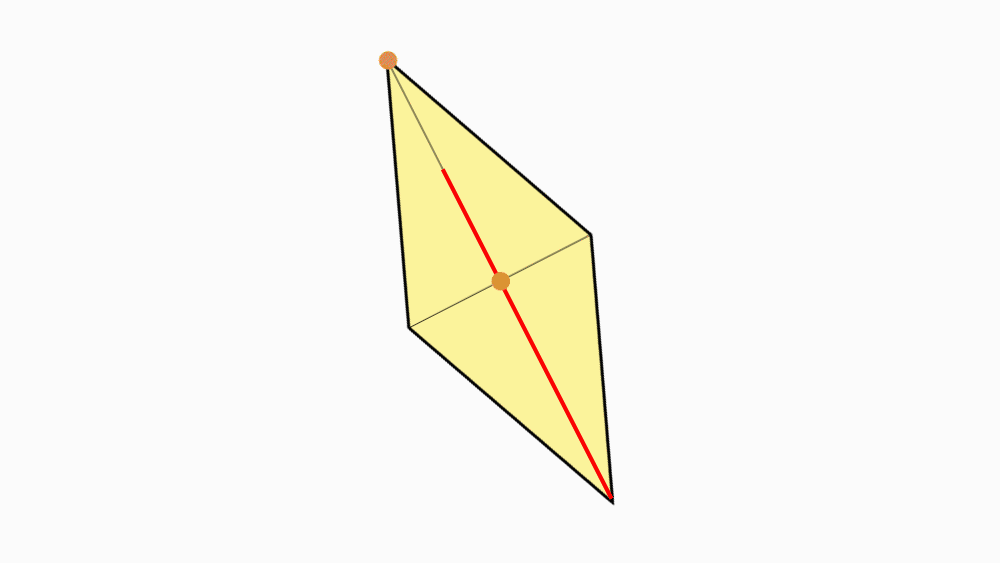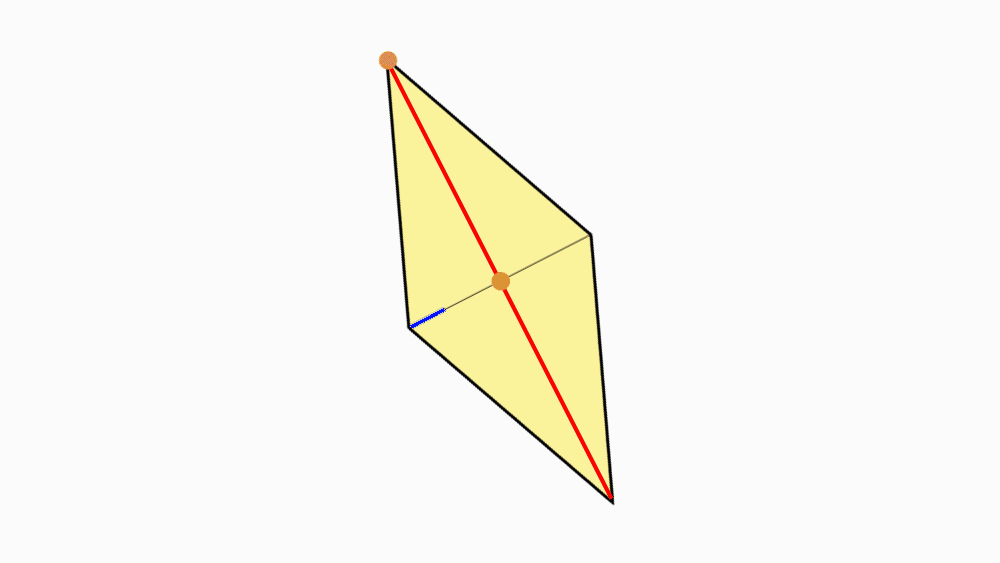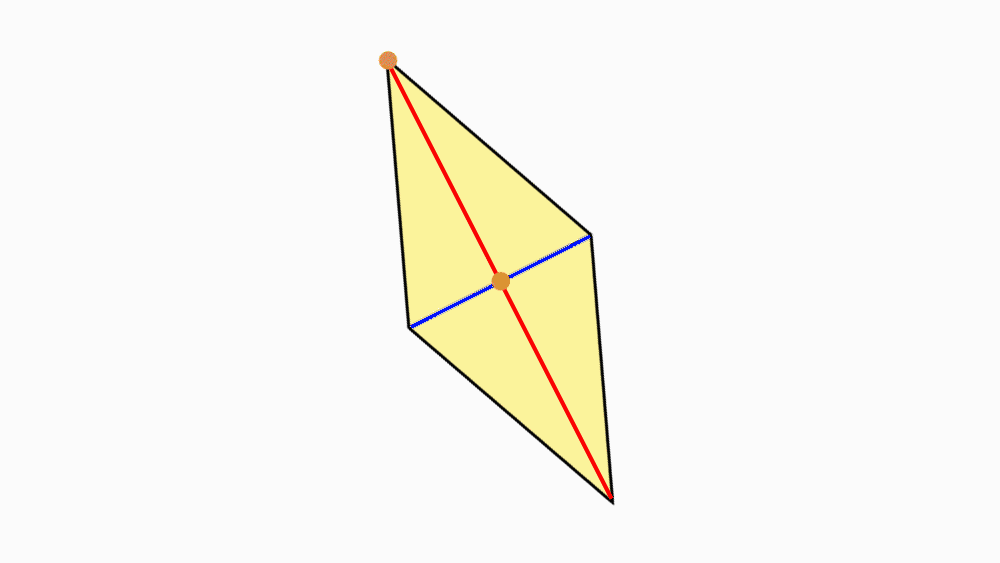
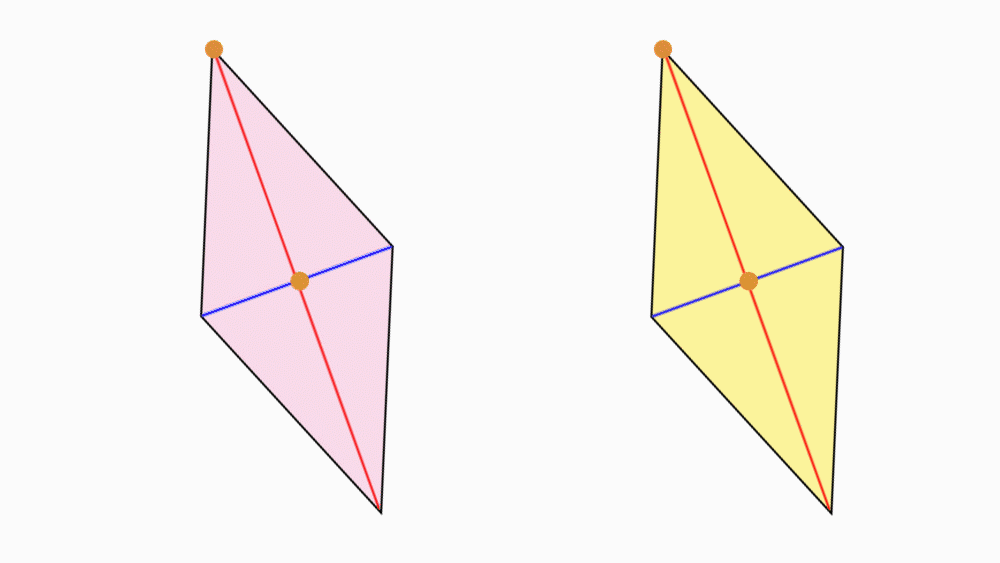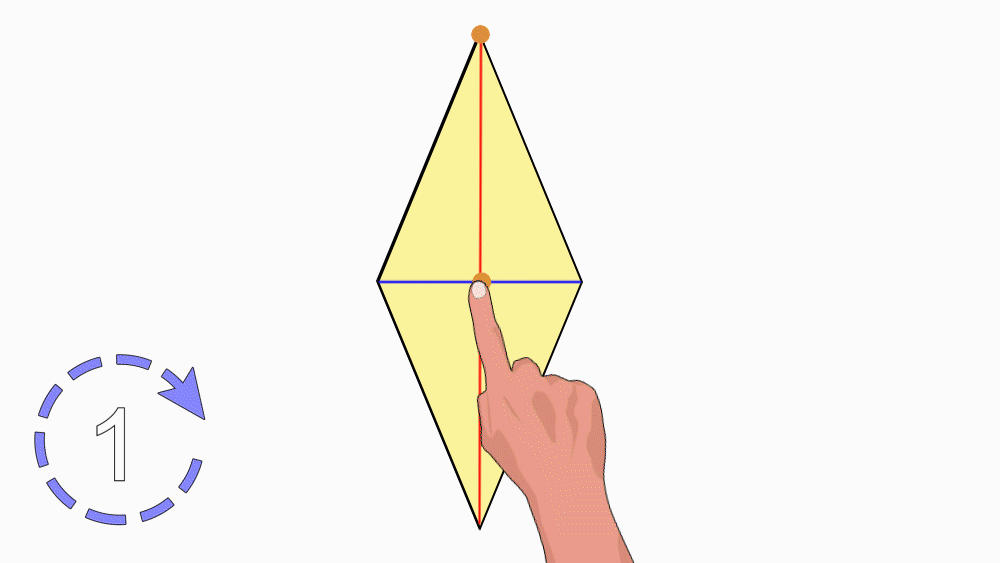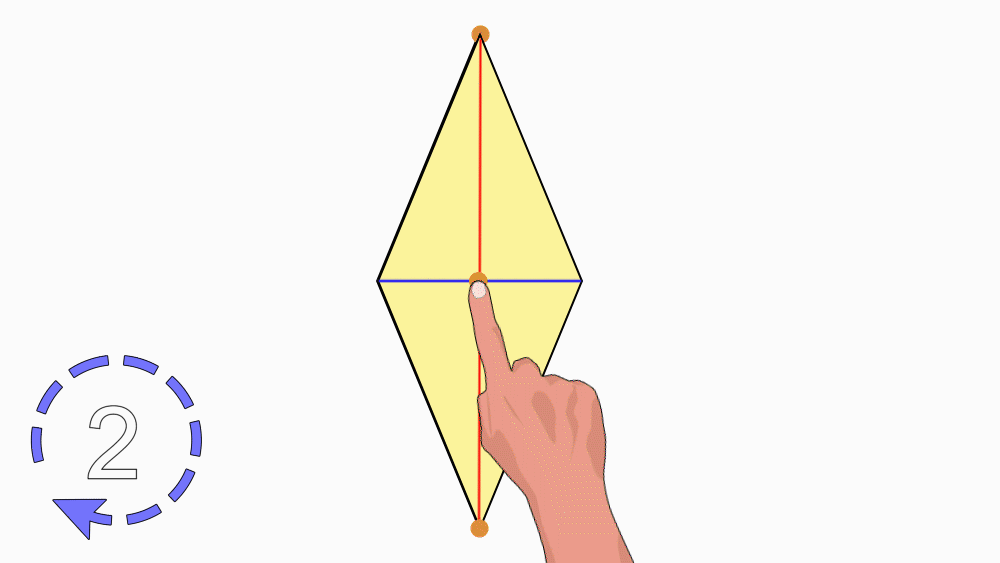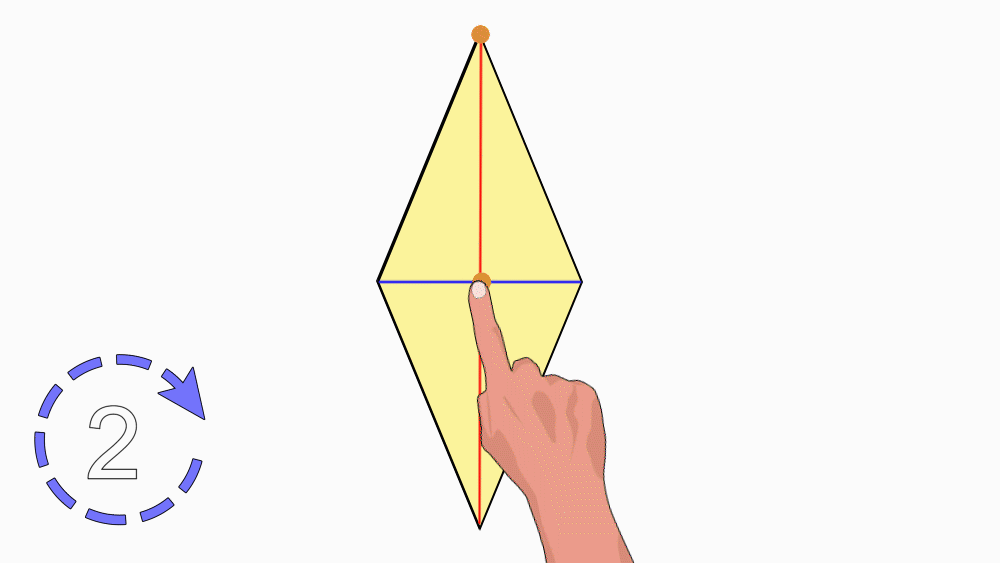
שאלה: מה ניתן לומר על שני הישרים המחברים את הקדקודים הנגדיים?

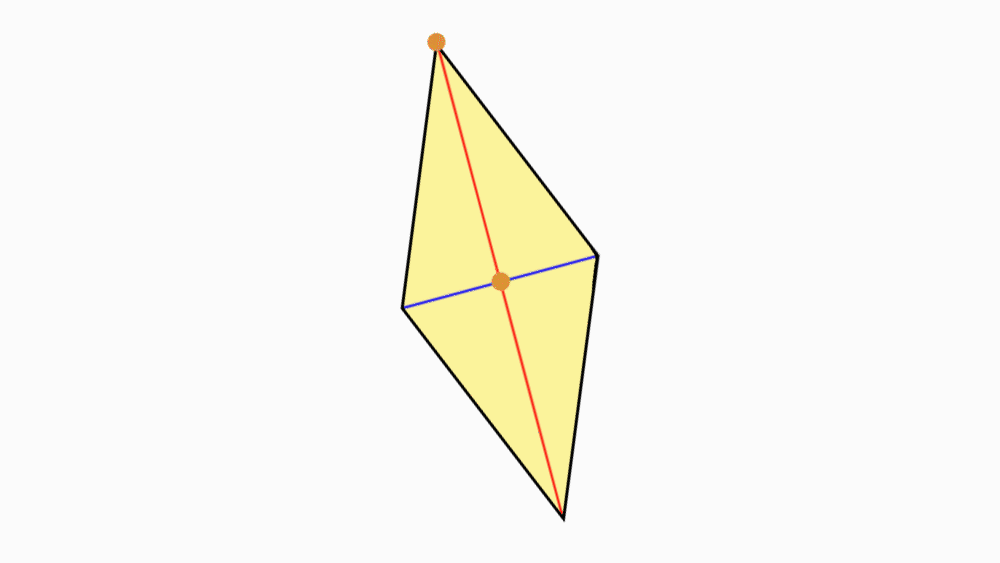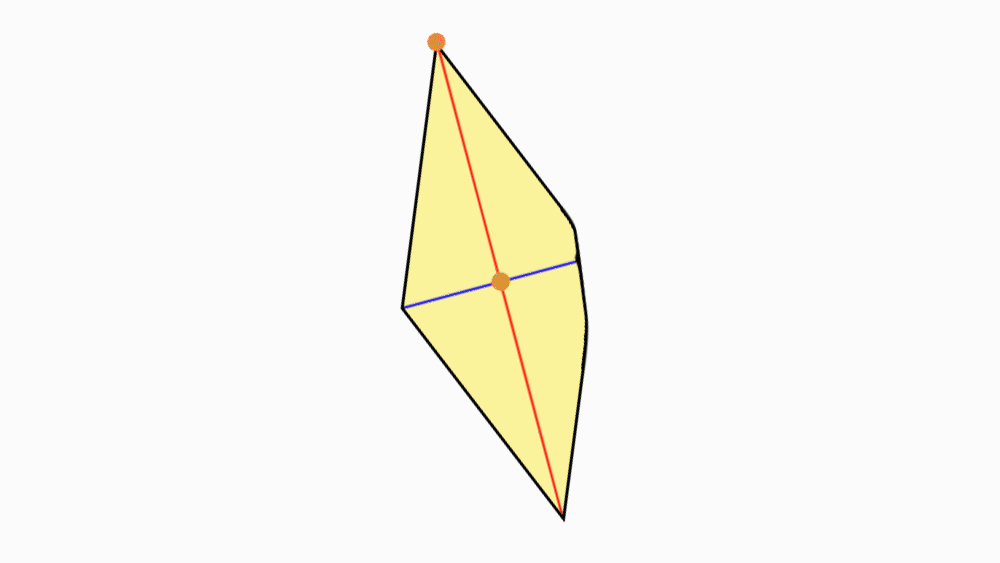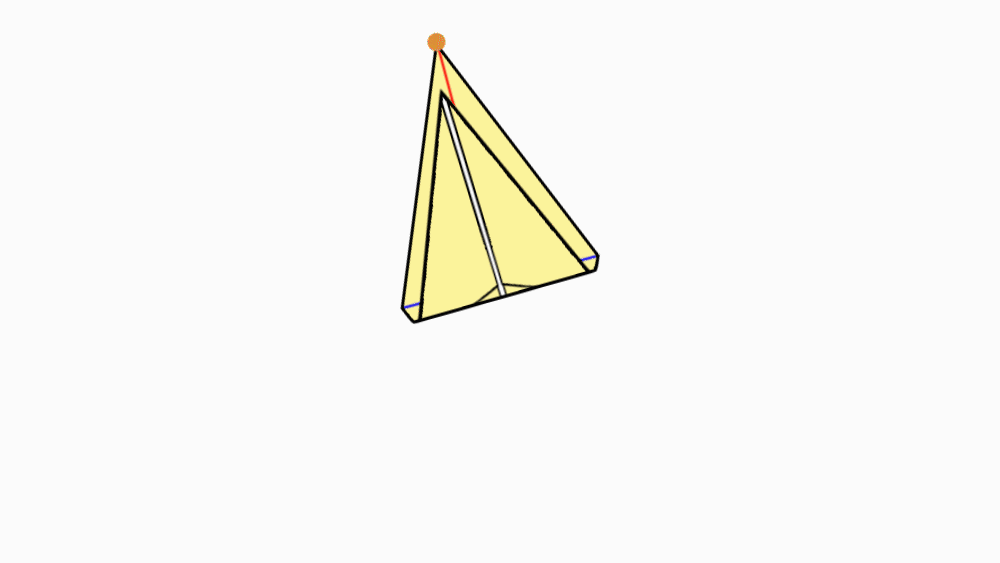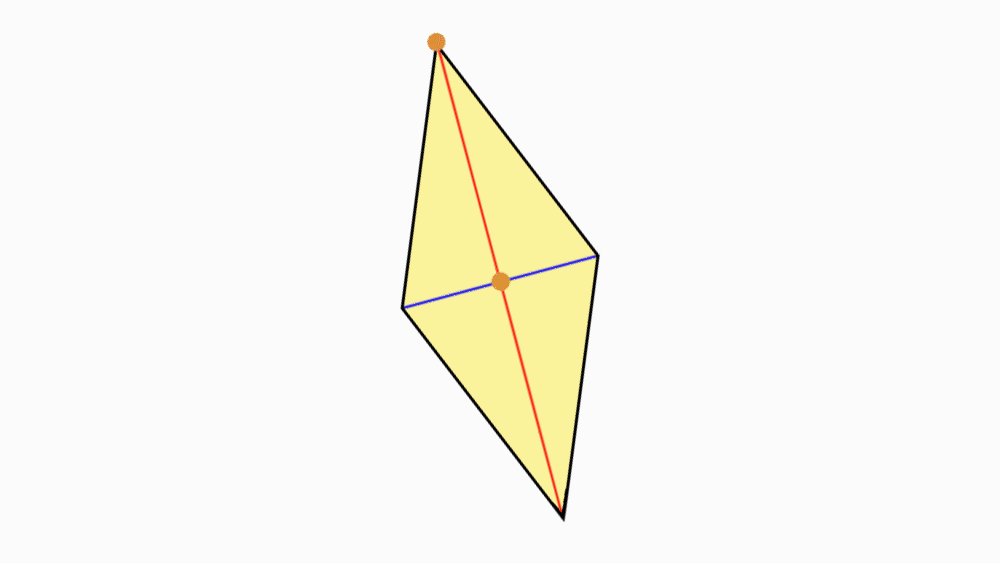
תשובה: שני הישרים הם קווי סימטריה של המעוין.

אם נקפל את המעוין לאורך כל אחד מקווי הסימטריה, משולש אחד יכסה את המשולש השני בדיוק.

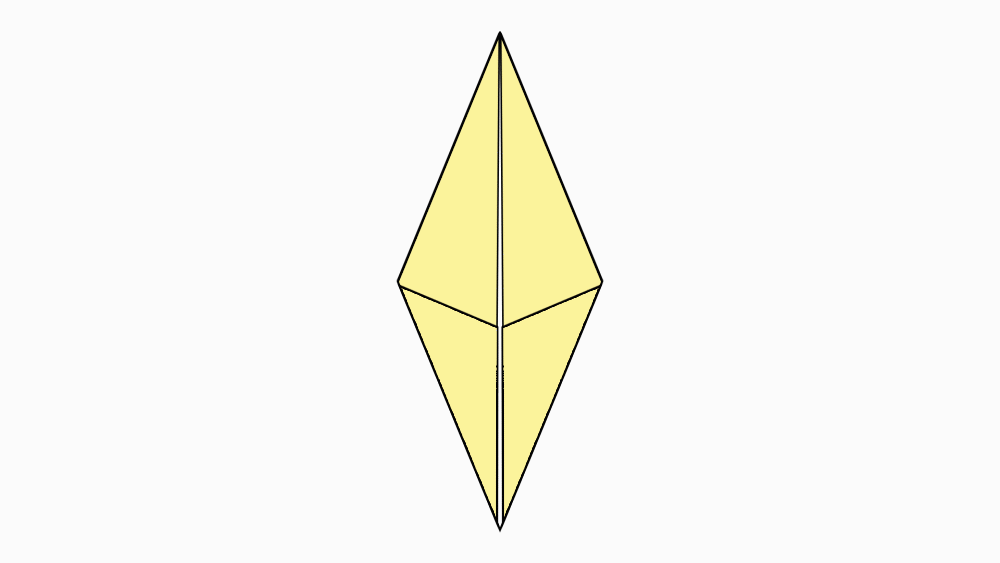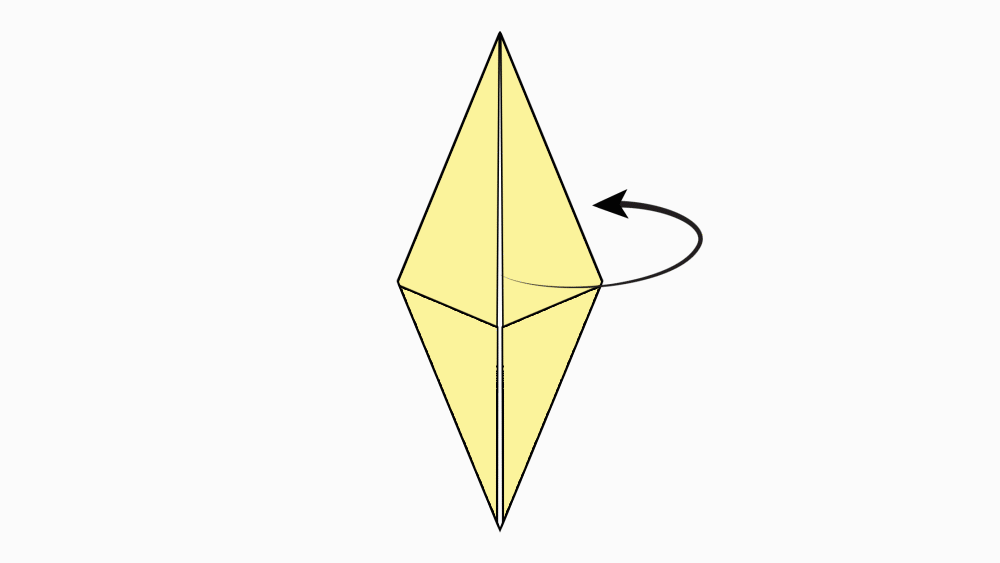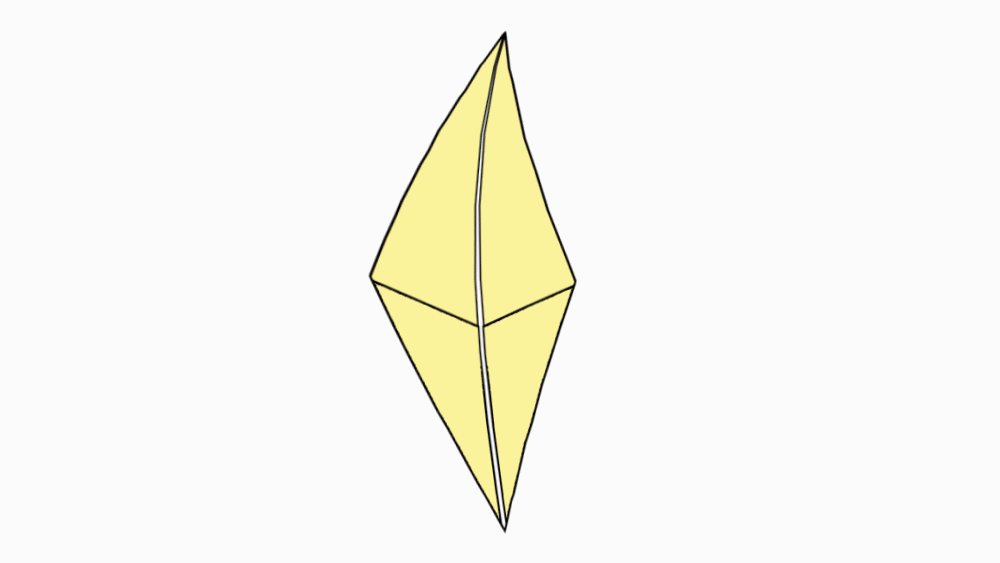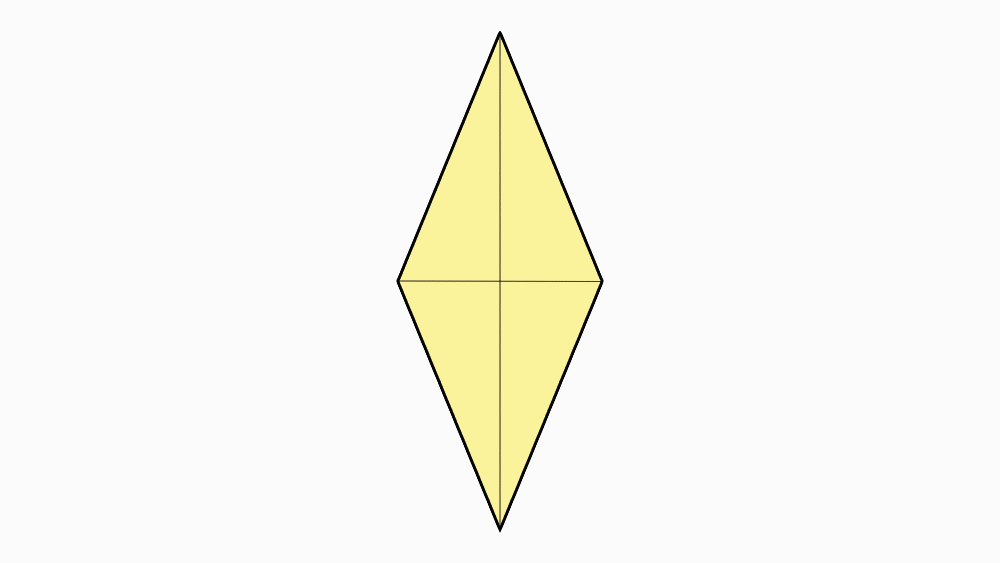
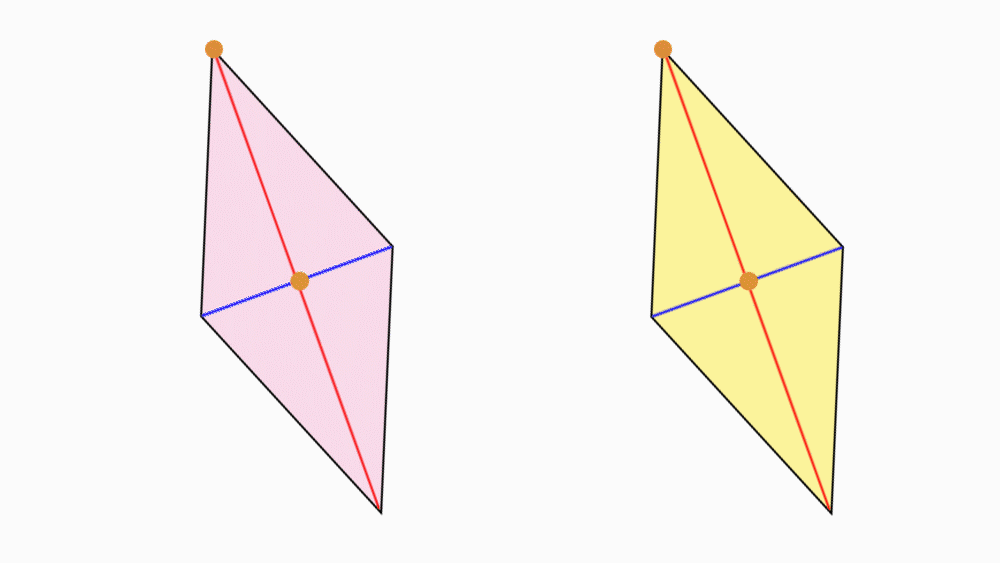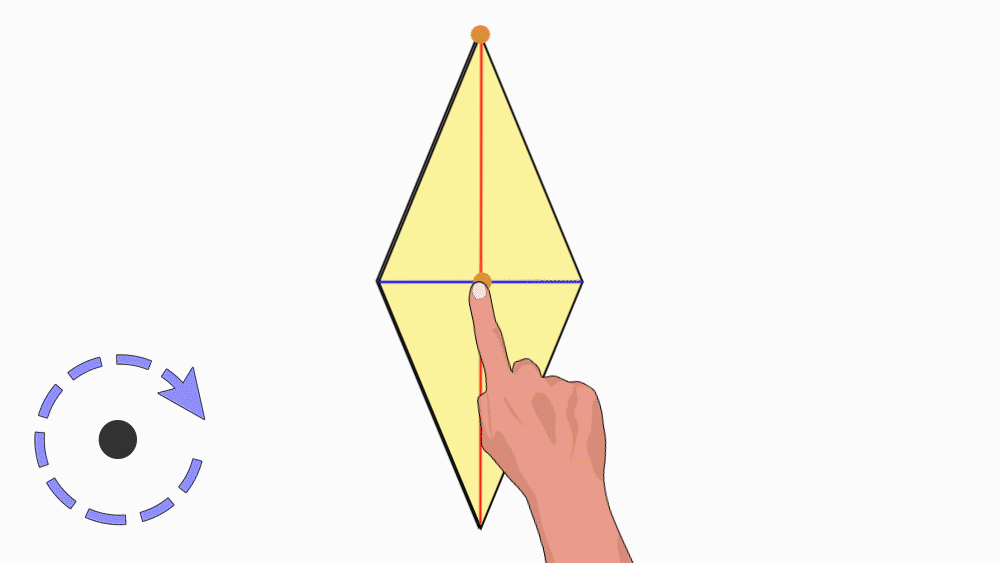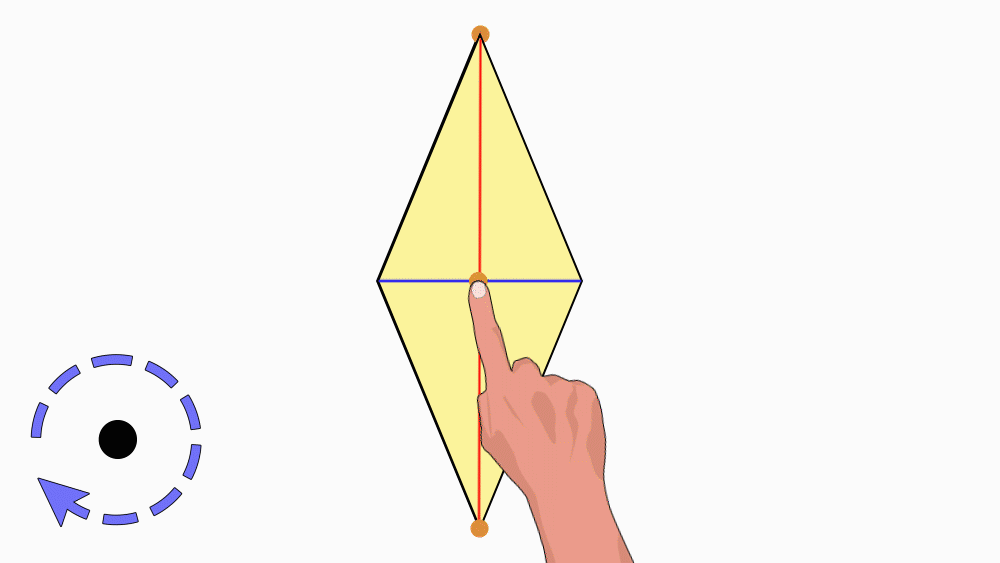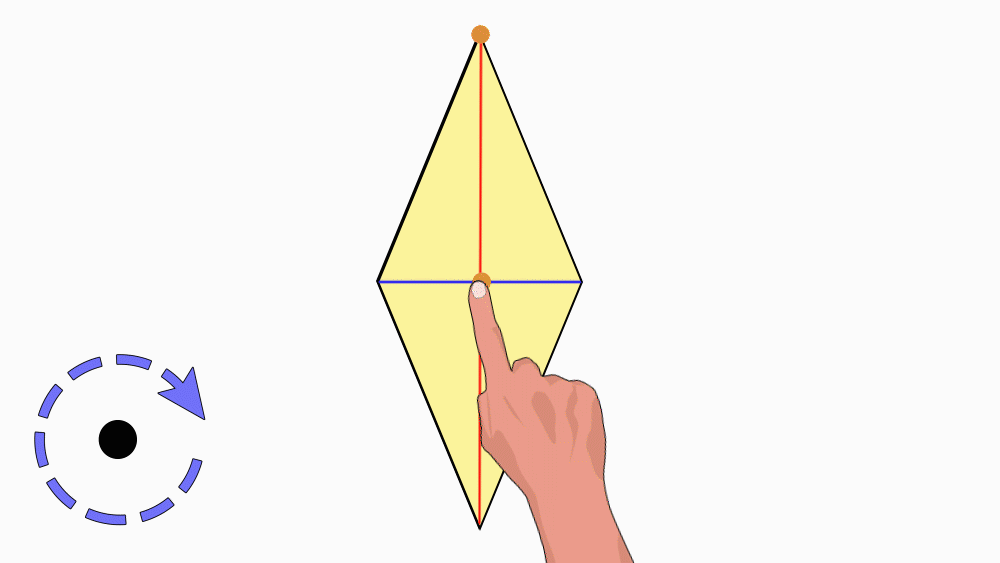
הנחיה: הניחו את שני המעוינים האחד מעל השני כך שהנקודות יהיו האחת על גבי השנייה. הציבו כלי כתיבה או אצבע בנקודת חיתוך קווי הסימטריה וסובבו את המעוין העליון.

שאלה לדיון: בחנו כמה פעמים מעוין אחד כיסה את המעוין השני במהלך סיבוב שלם? הסבירו.

תשובה: במהלך סיבוב שלם מעוין אחד כיסה את המעוין השני פעמיים.  דרגת הסיבוב היא 2. לכן, למעוין יש סימטריה סיבובית.

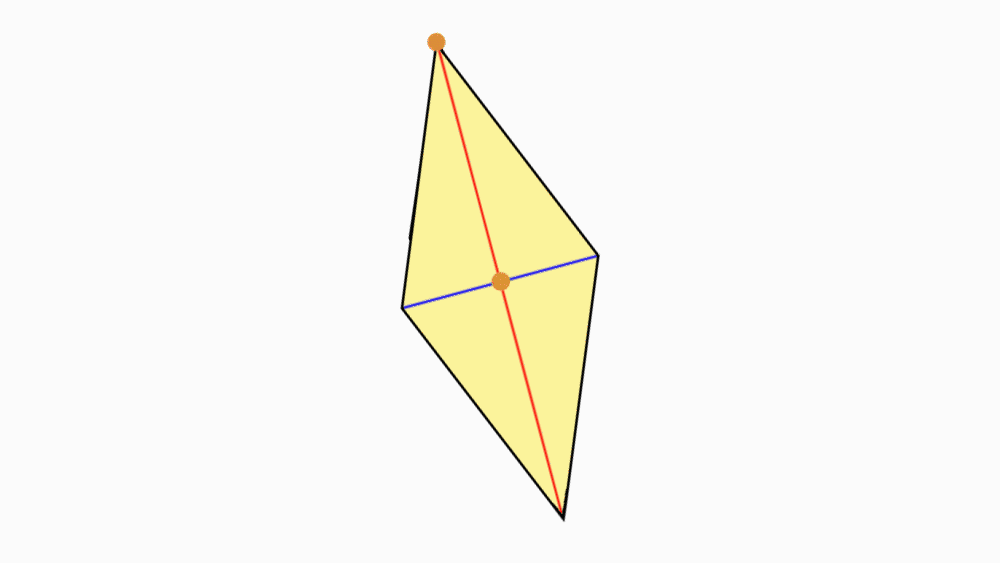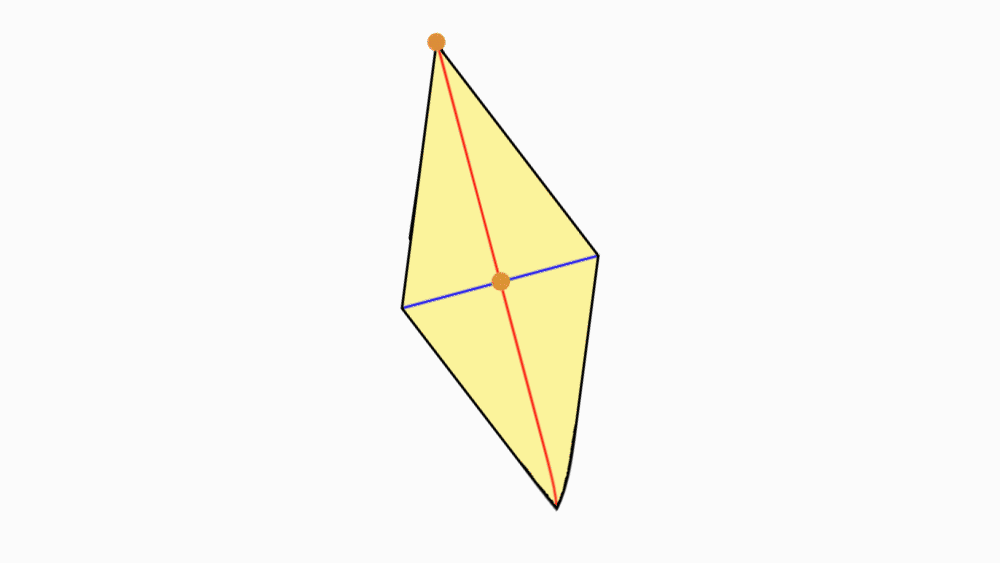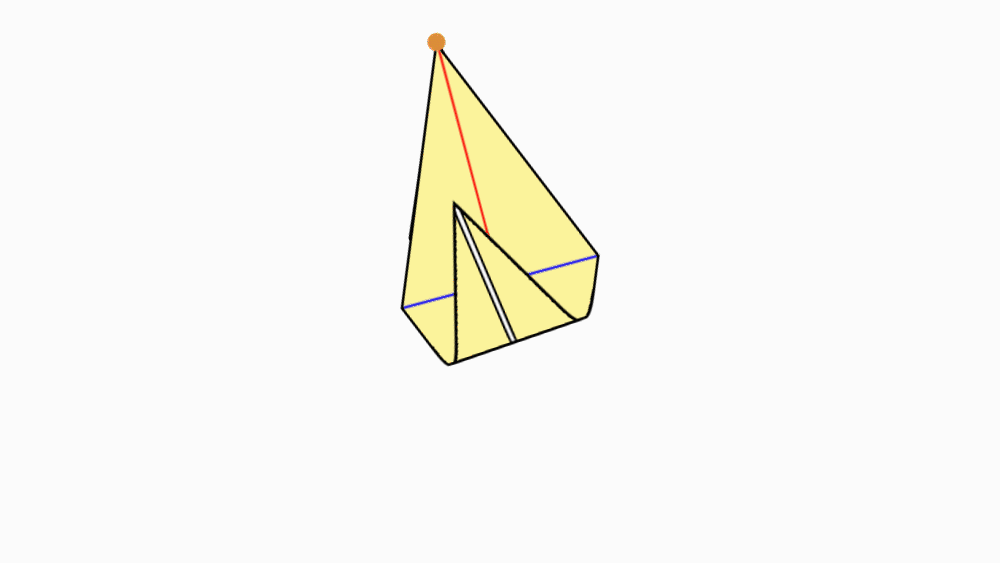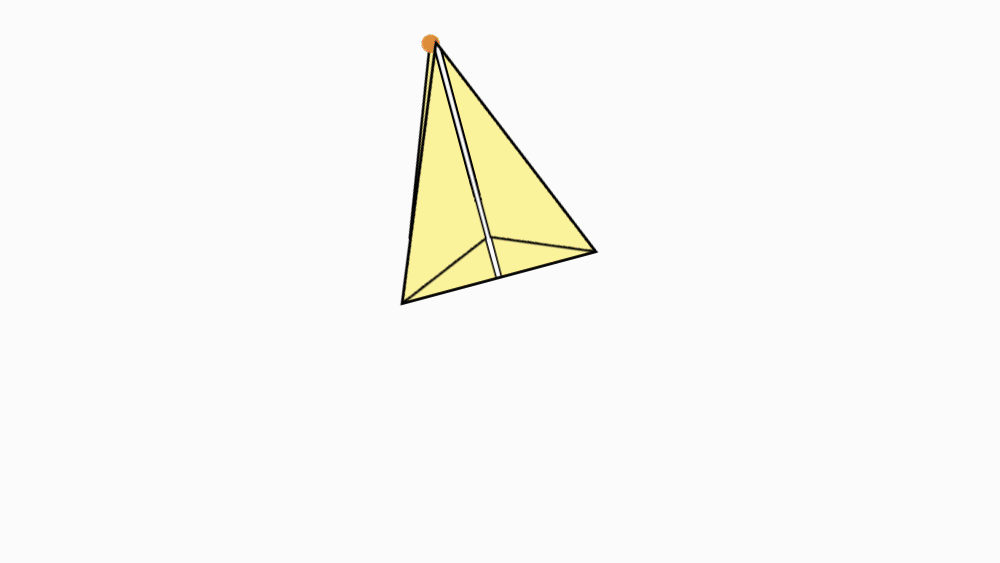
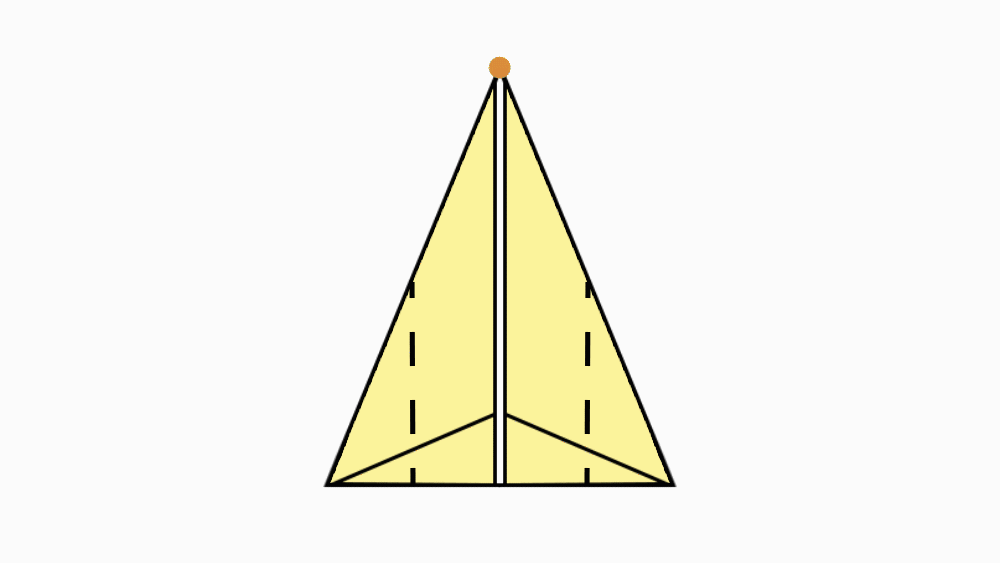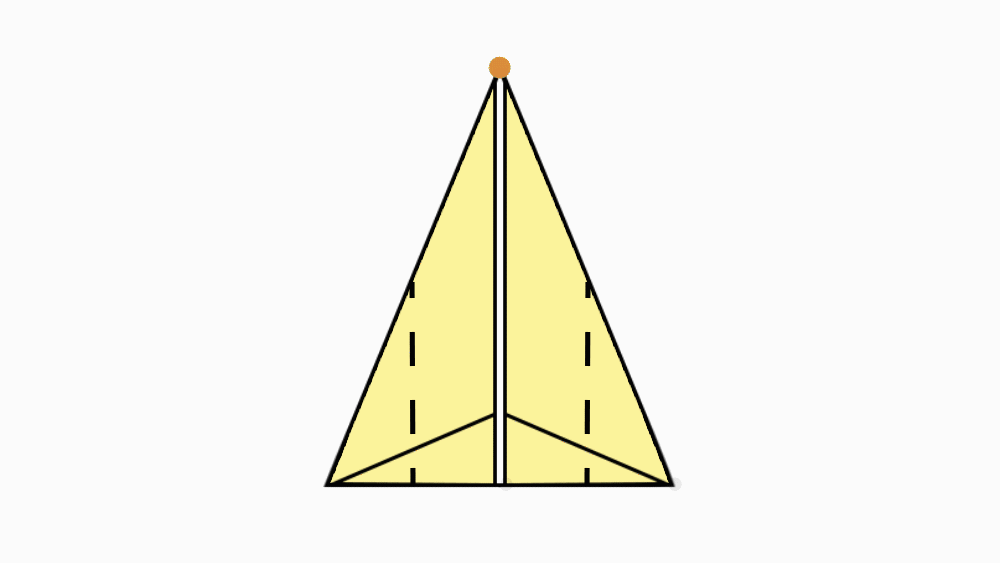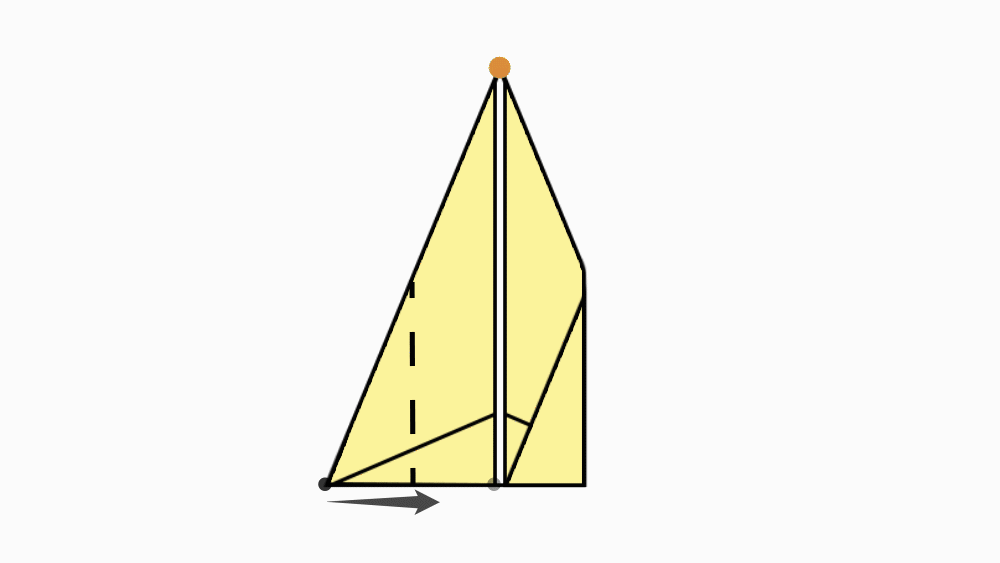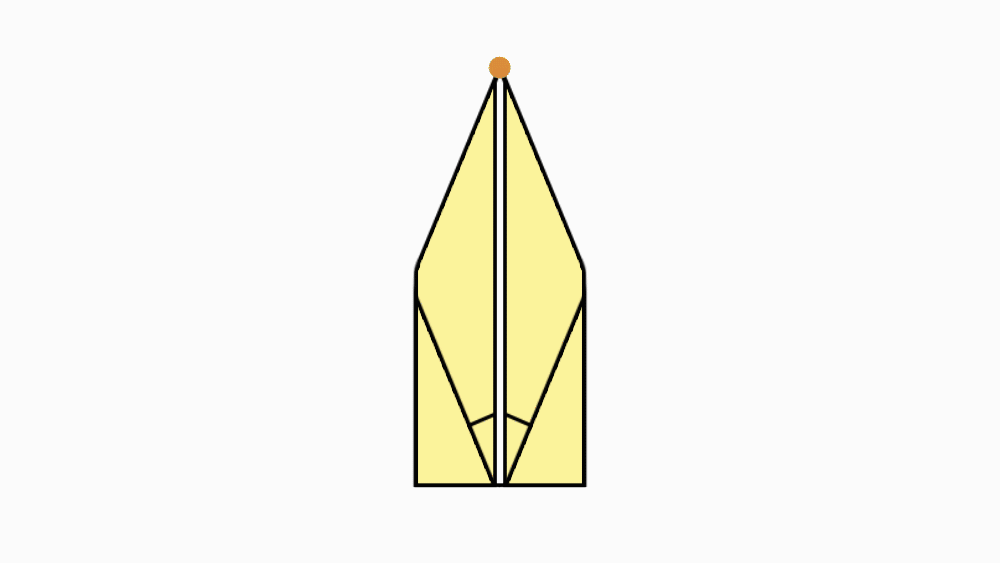
הוראת קיפול: להצמיד קדקוד אל הקדקוד הנגדי של האלכסון הארוך, כך שיתקבל משולש.

הוראת קיפול: לקפל את שני הקדקודים המסומנים אל קו הסימטריה של המשולש.

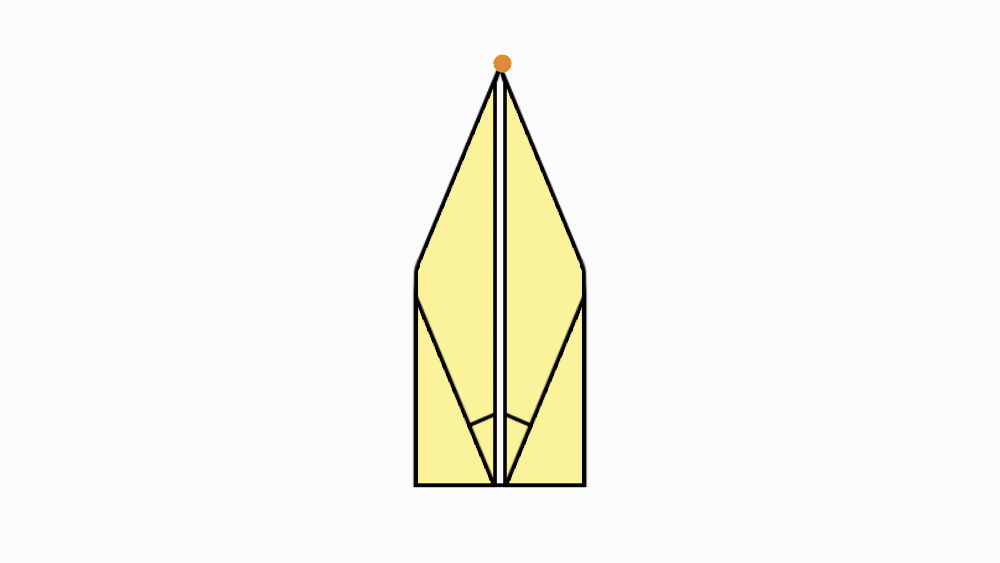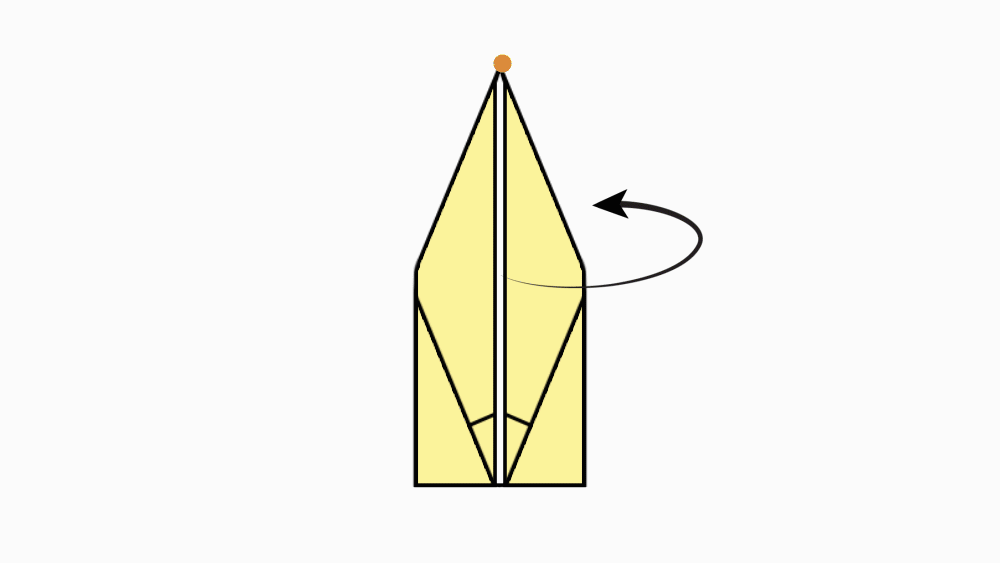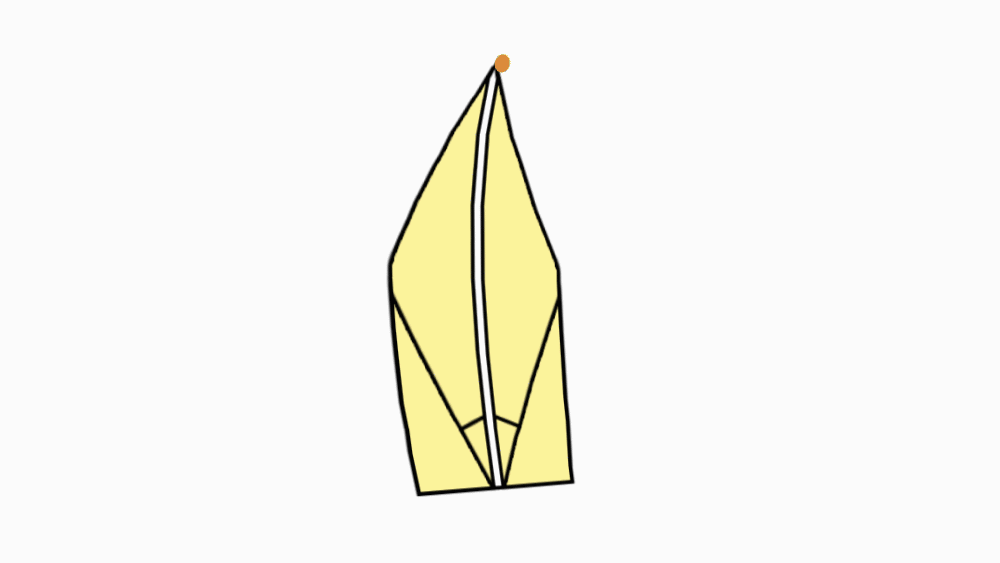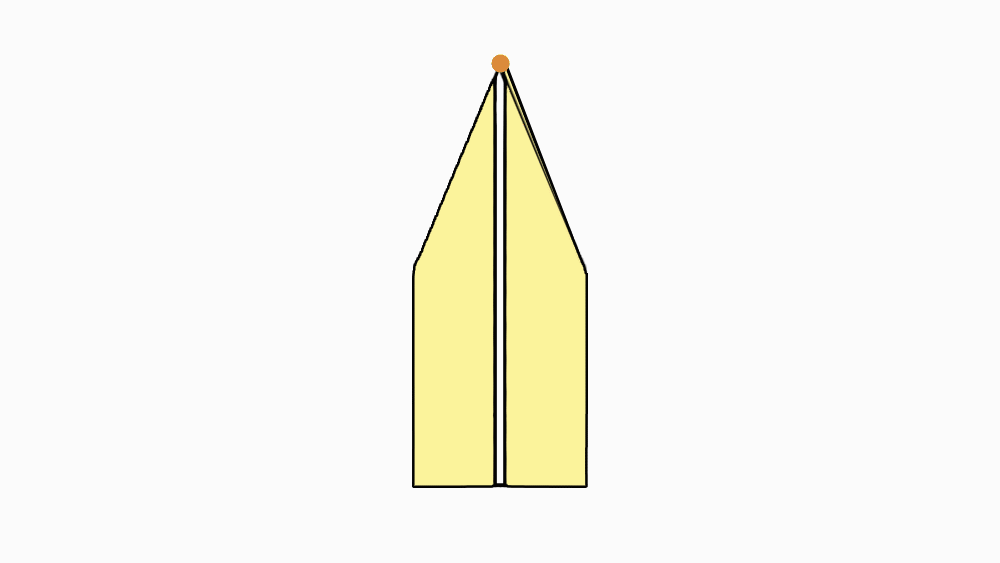
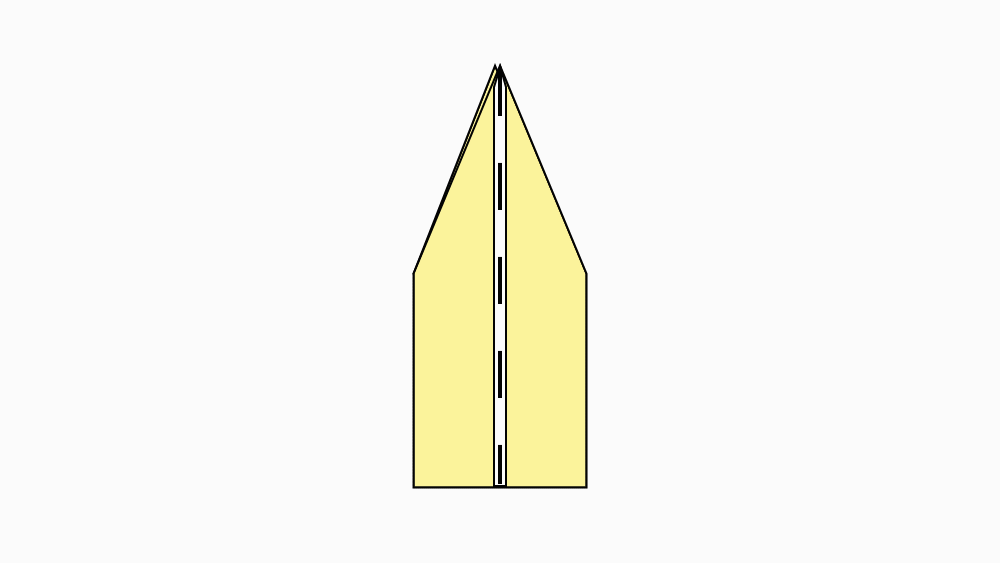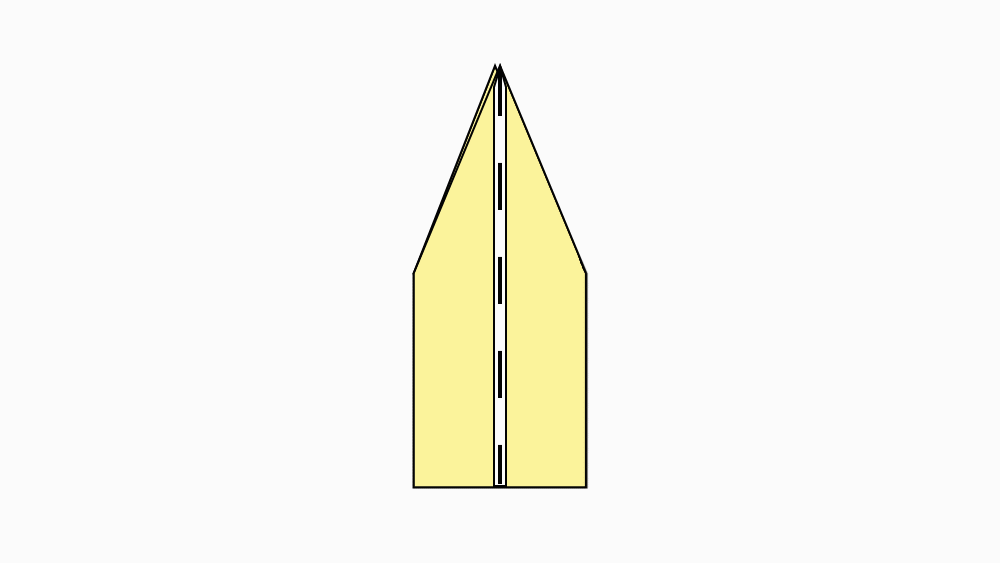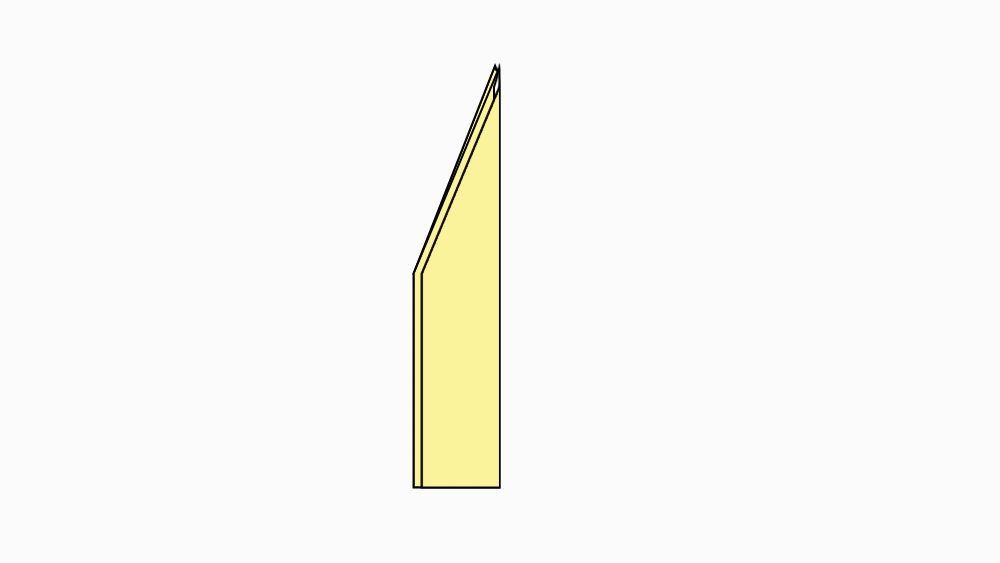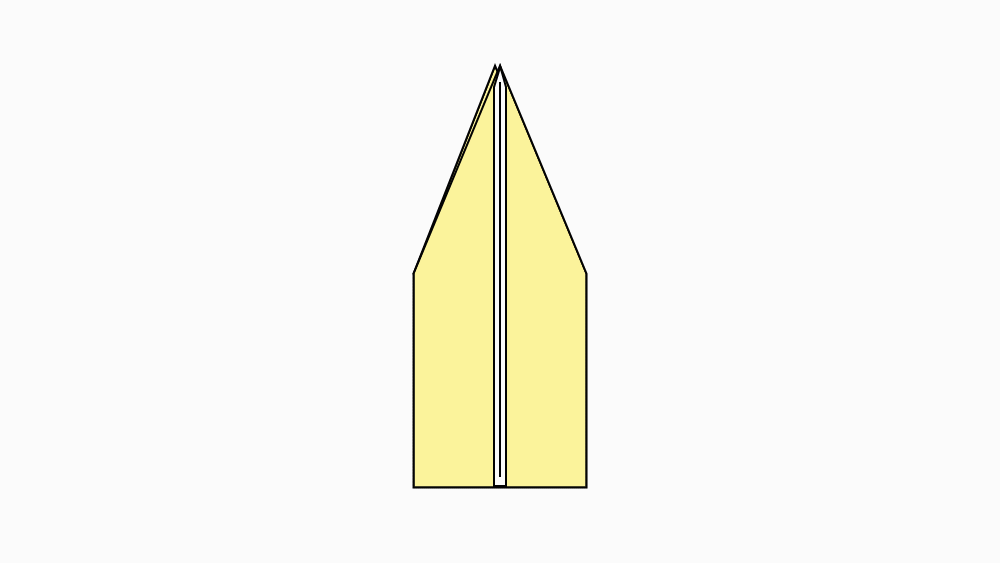
הוראת קיפול: להפוך את הנייר לצד השני.

הוראת קיפול: לקפל צלע ארוכה של המחומש המקופל אל הצלע המקבילה, לפתוח ולהפוך לצד השני.

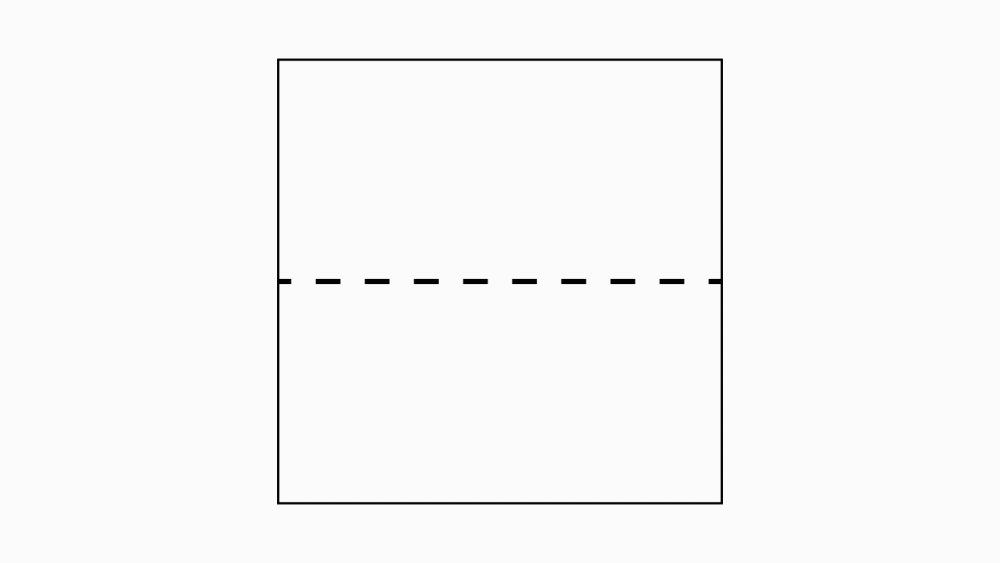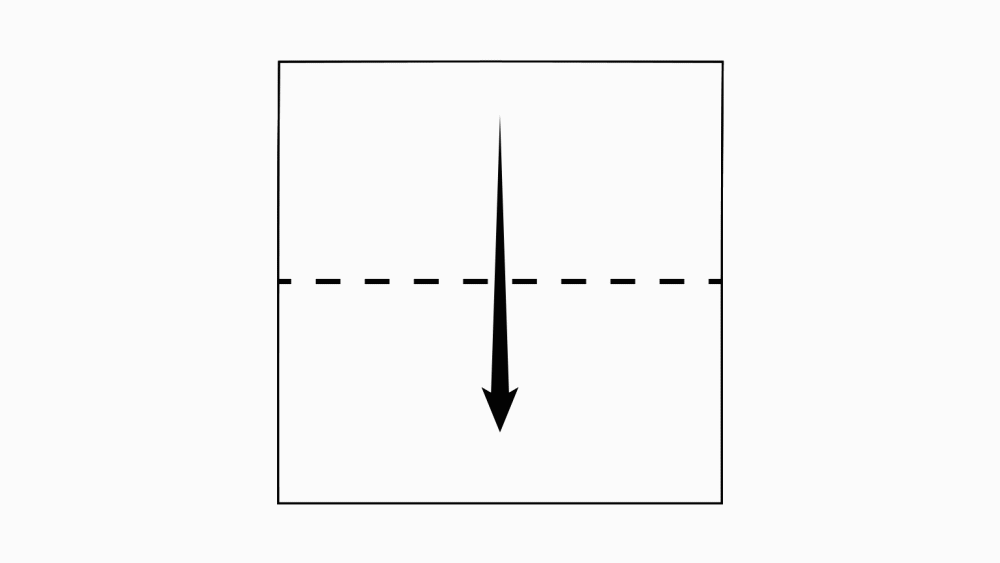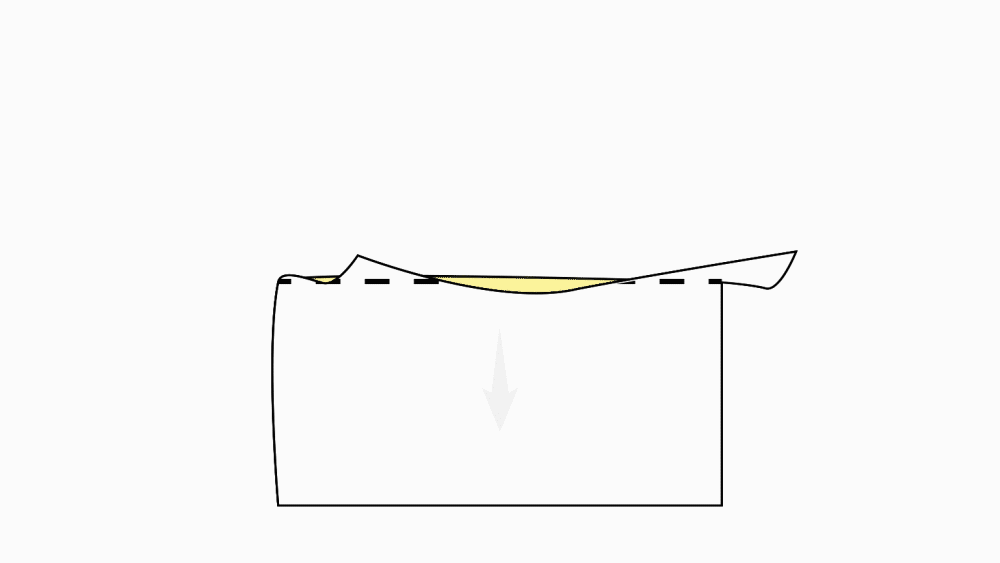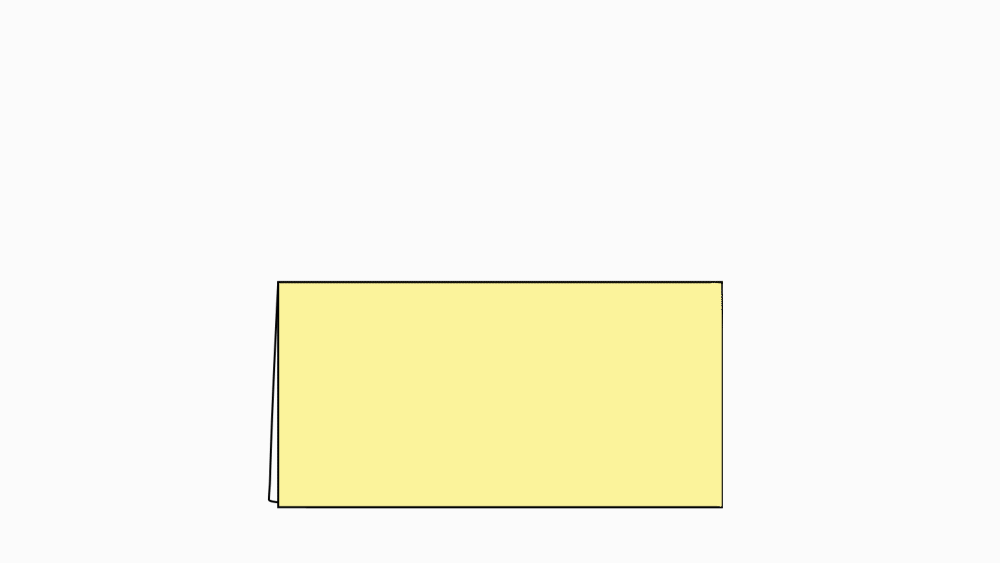
נבחר נייר קטן (10/10) ממניפת הדפים.

הוראת קיפול: להצמיד צלע אל צלע המקבילה.

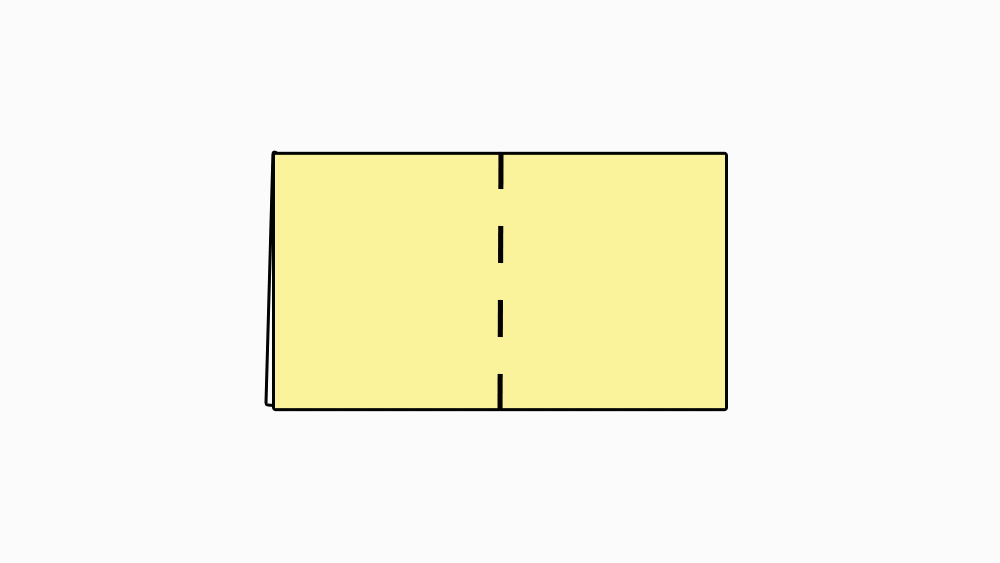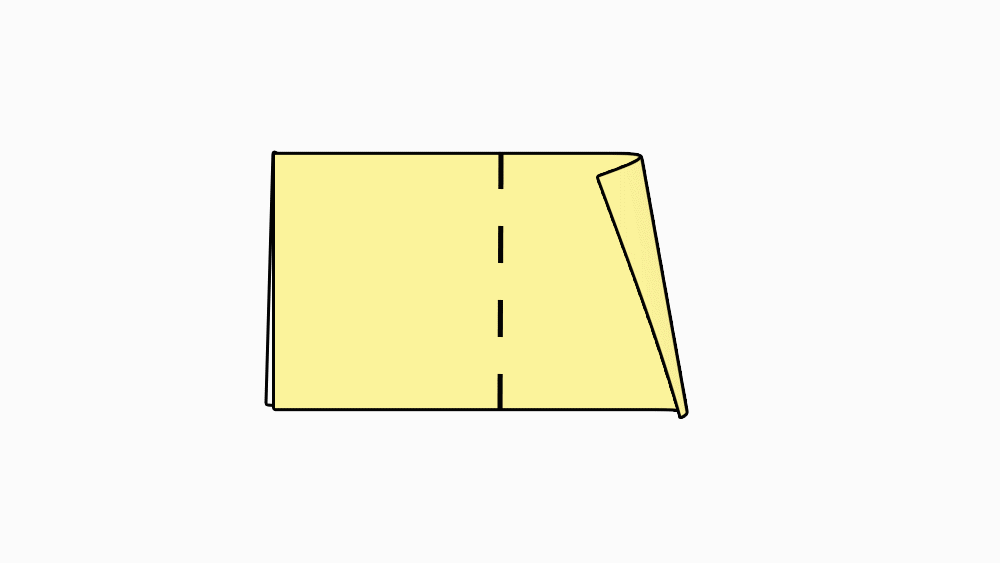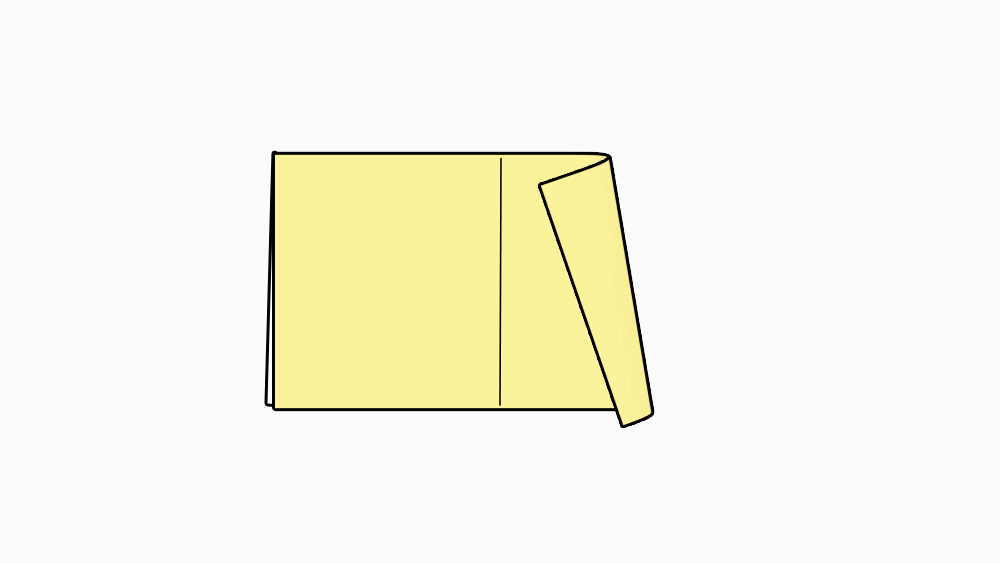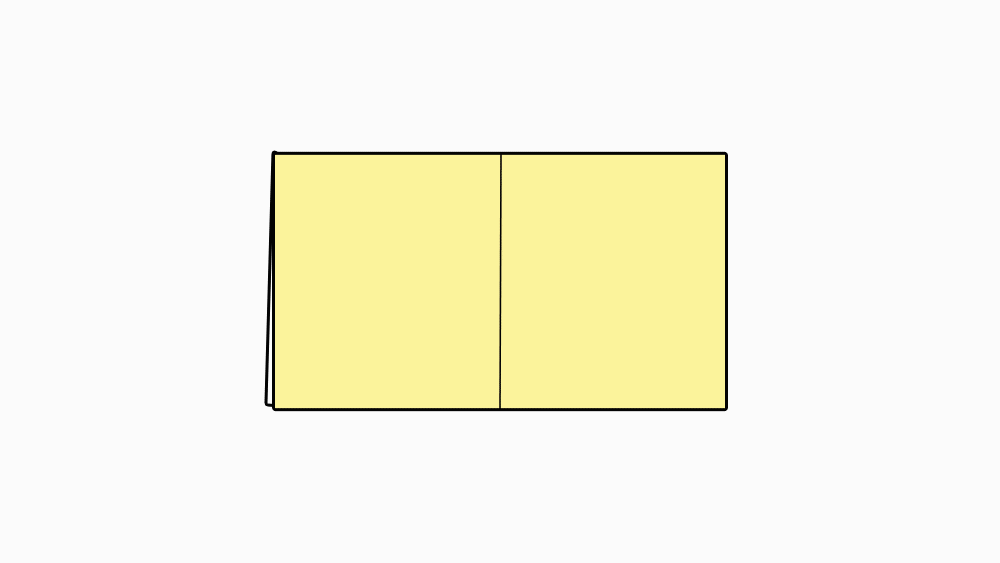
הוראת קיפול: לקפל ולפתוח צלע קצרה אל הצלע המקבילה ולפתוח לריבוע.

הוראת קיפול: להצמיד  קדקוד אל קדקוד נגדי.

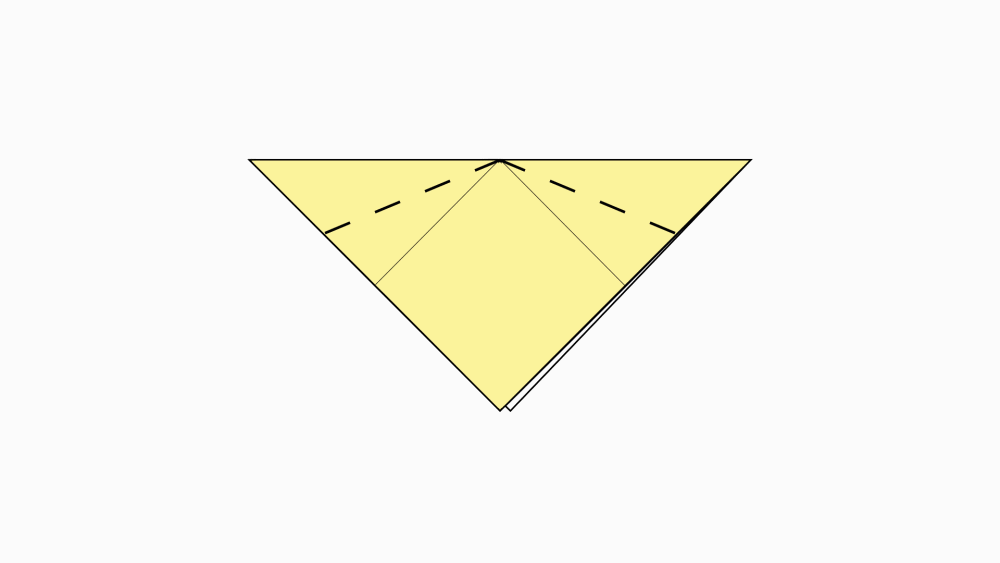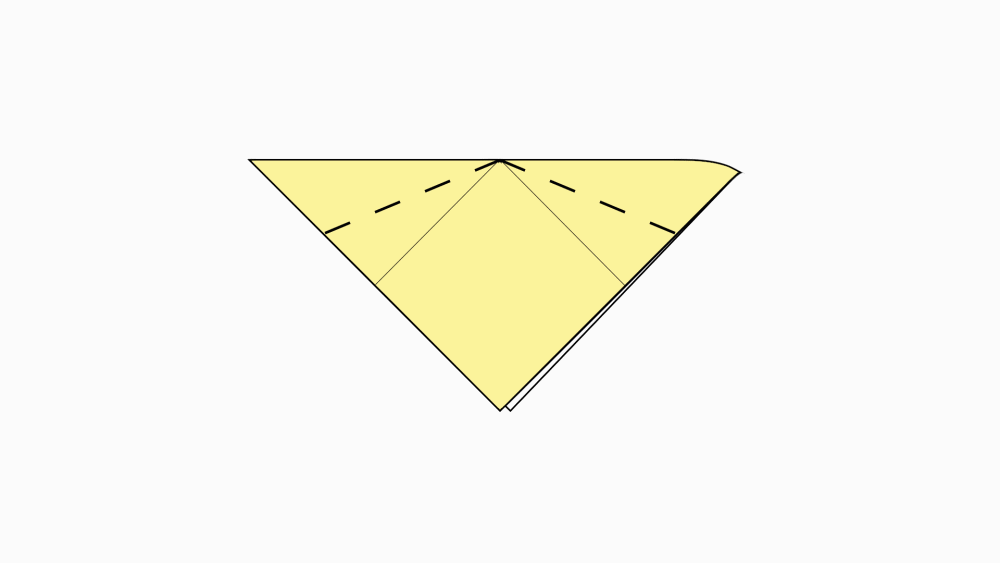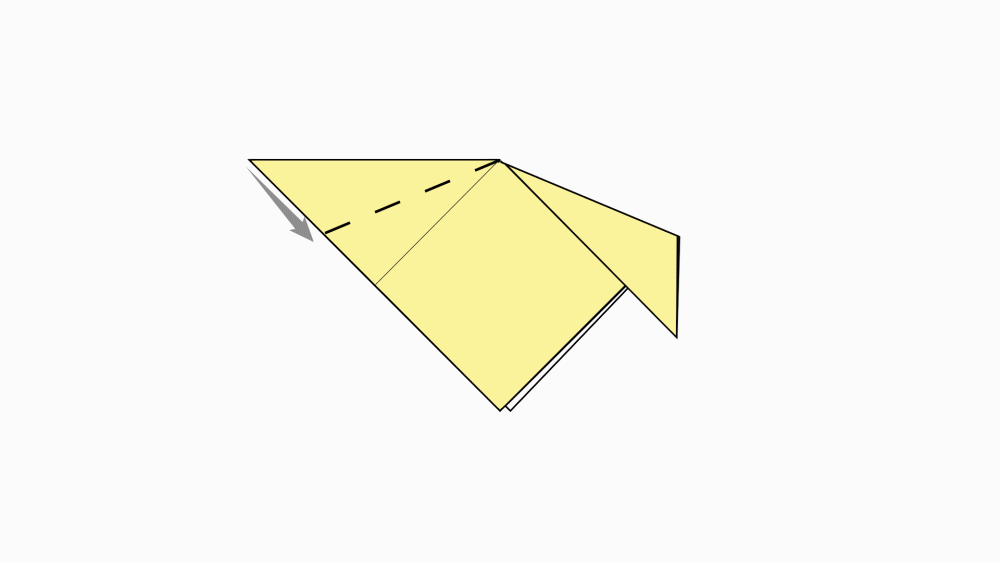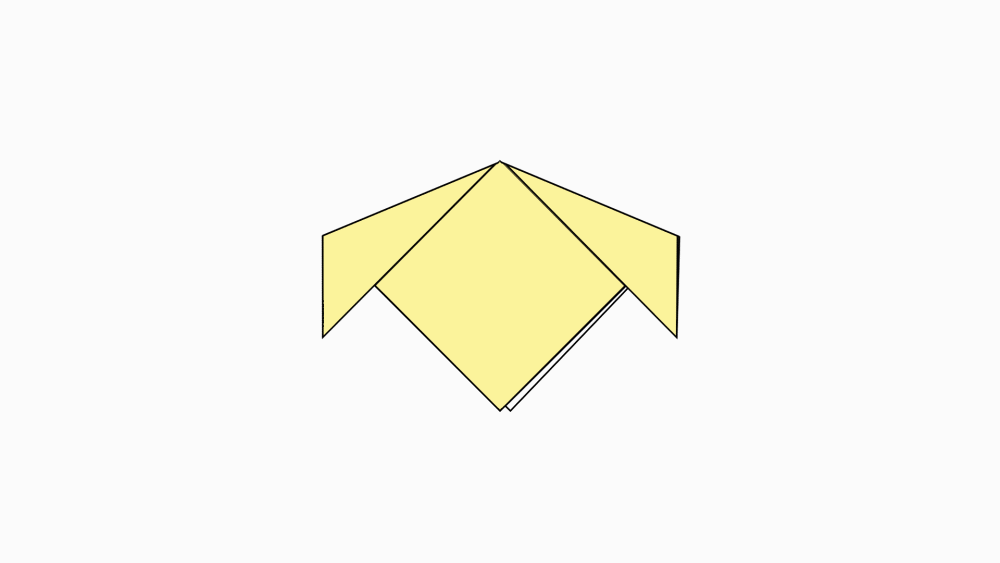
הוראת קיפול: לקפל לפי הסימון.

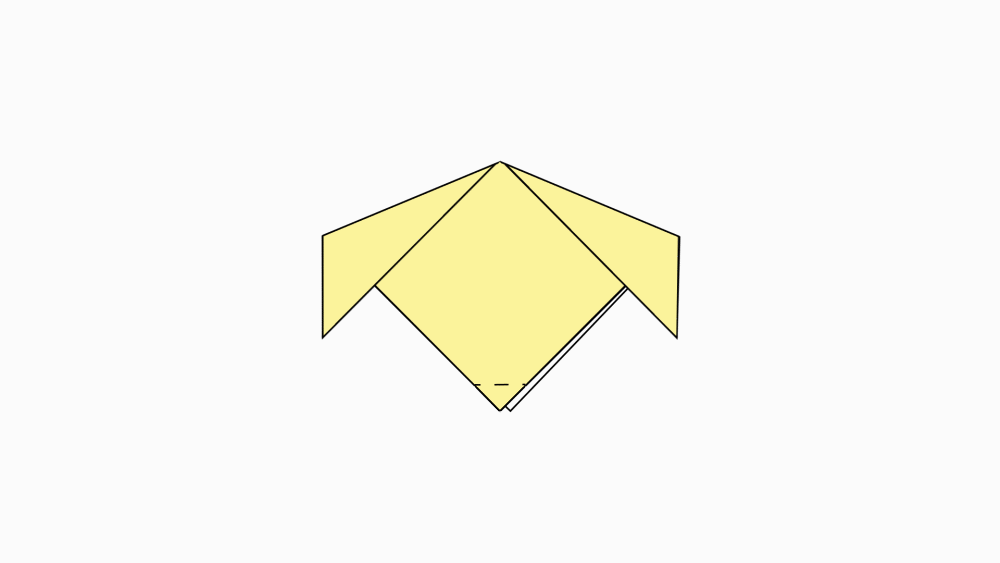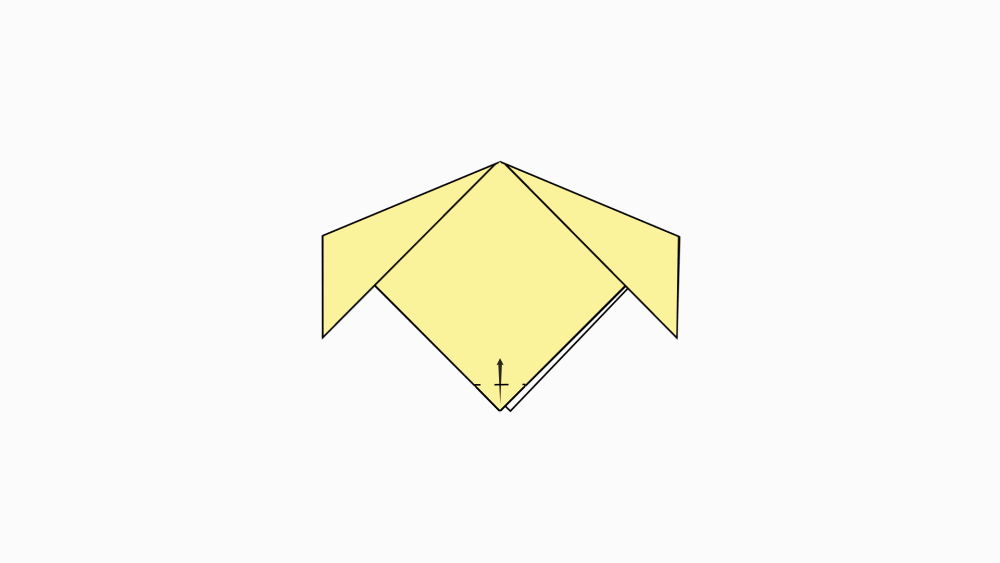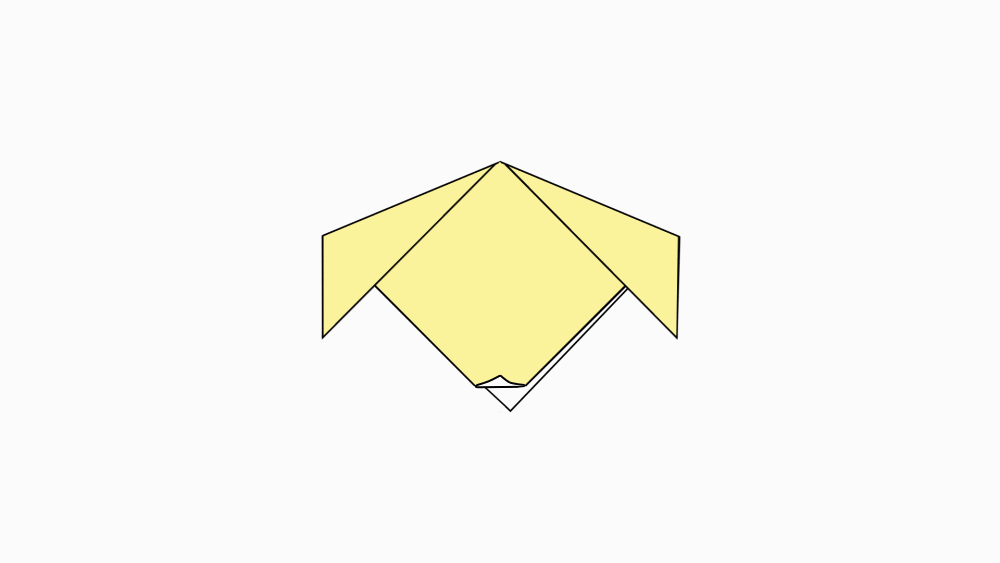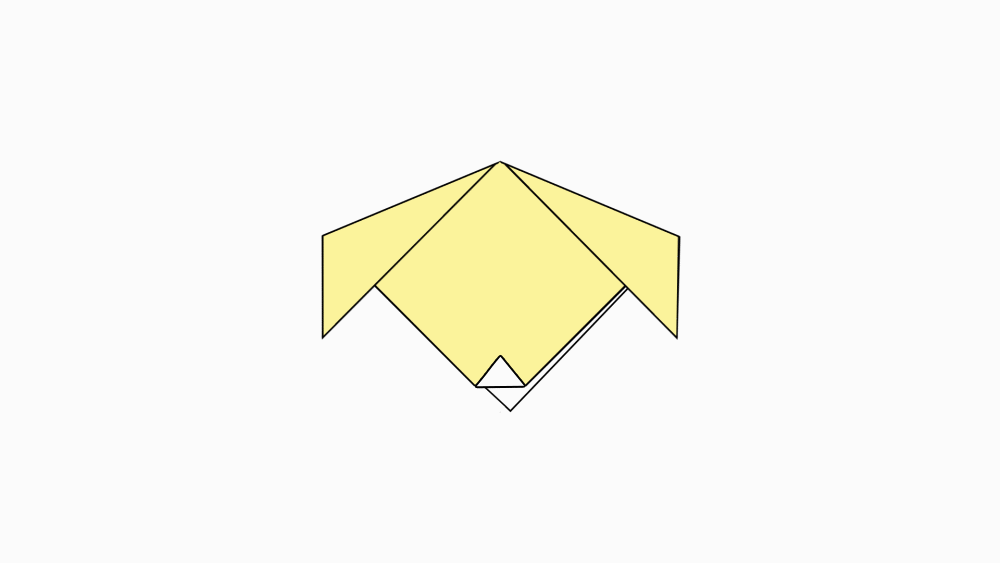
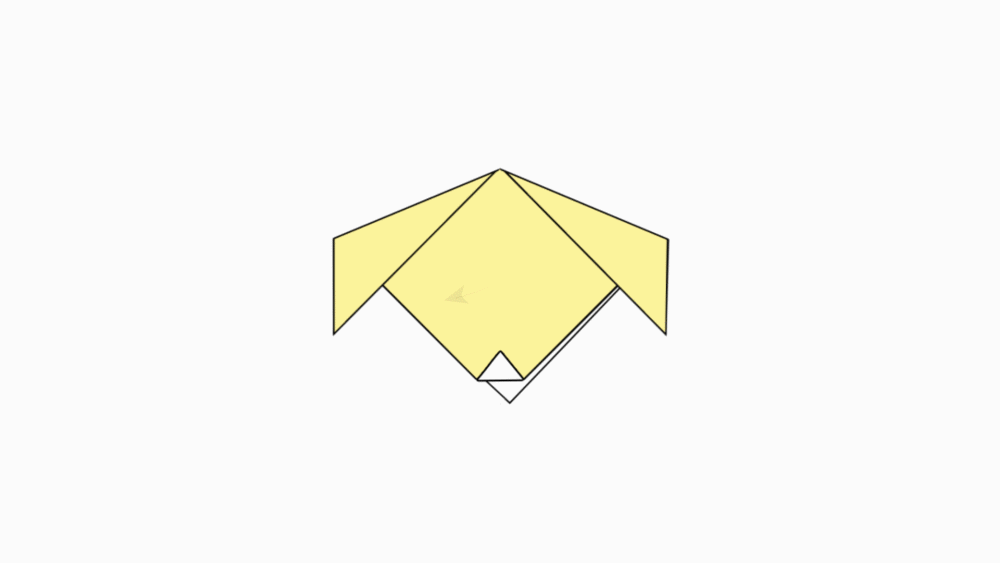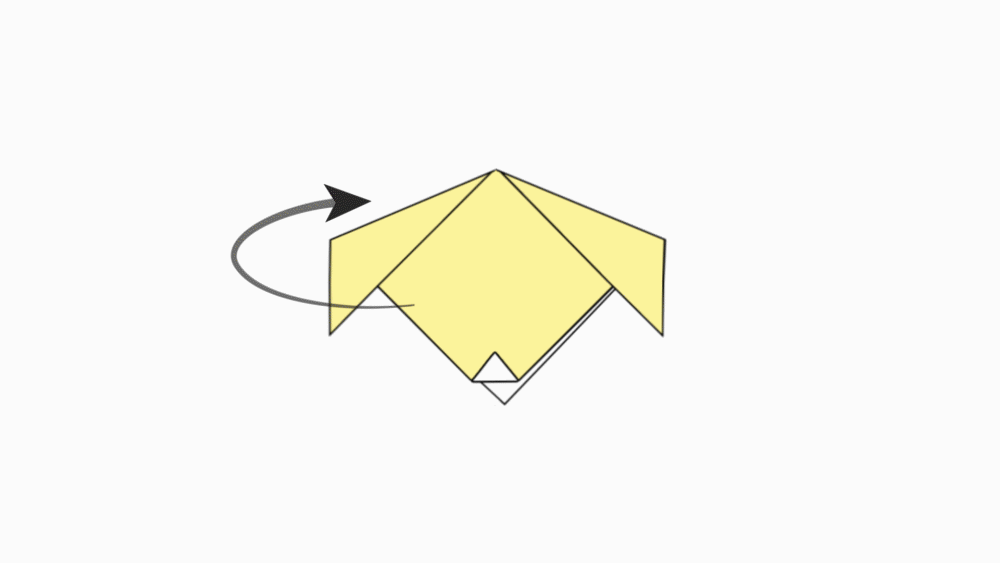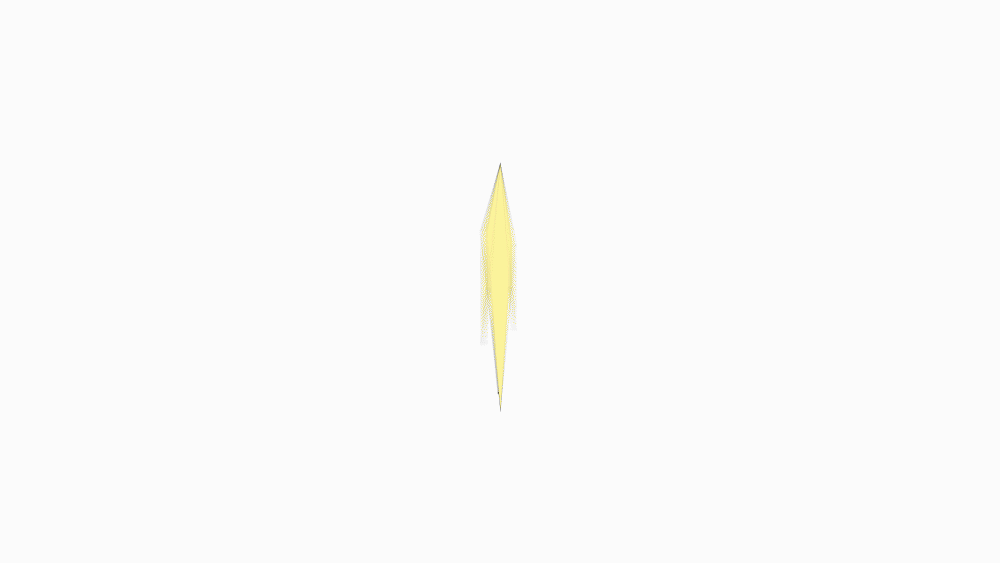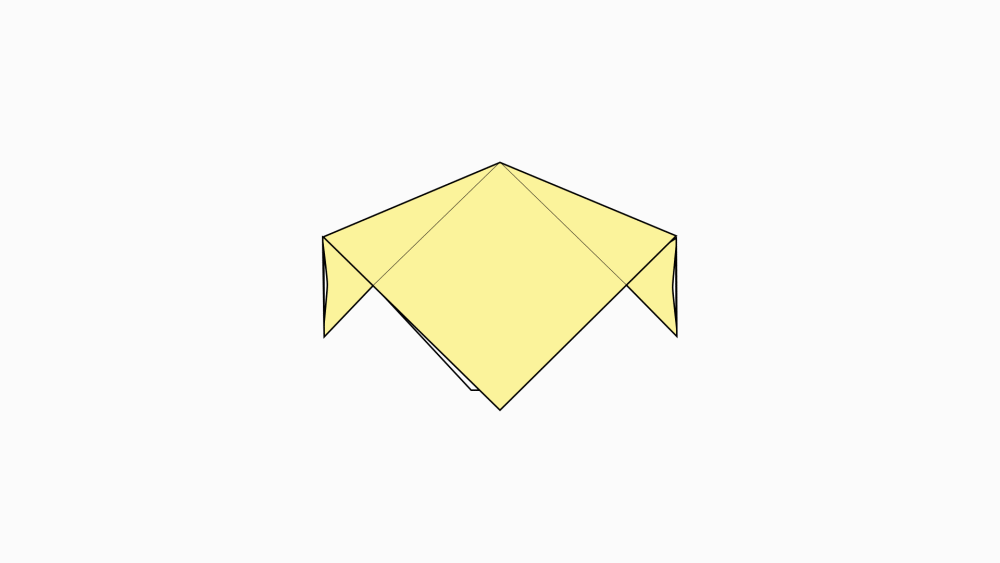
הוראת קיפול: לקפל את הקדקוד של הזווית הישרה למשולש קטן.

הוראת קיפול: להפוך לצד השני.

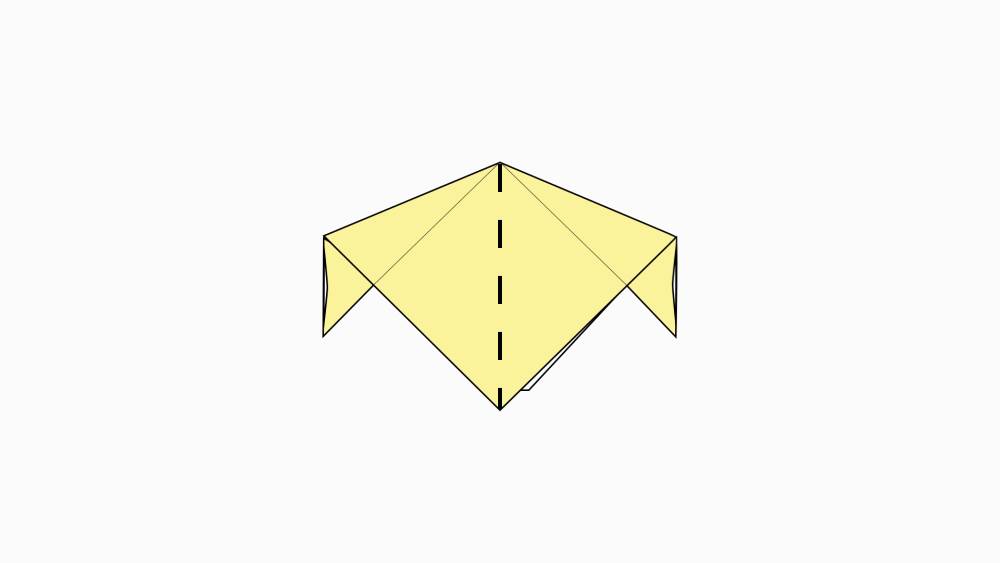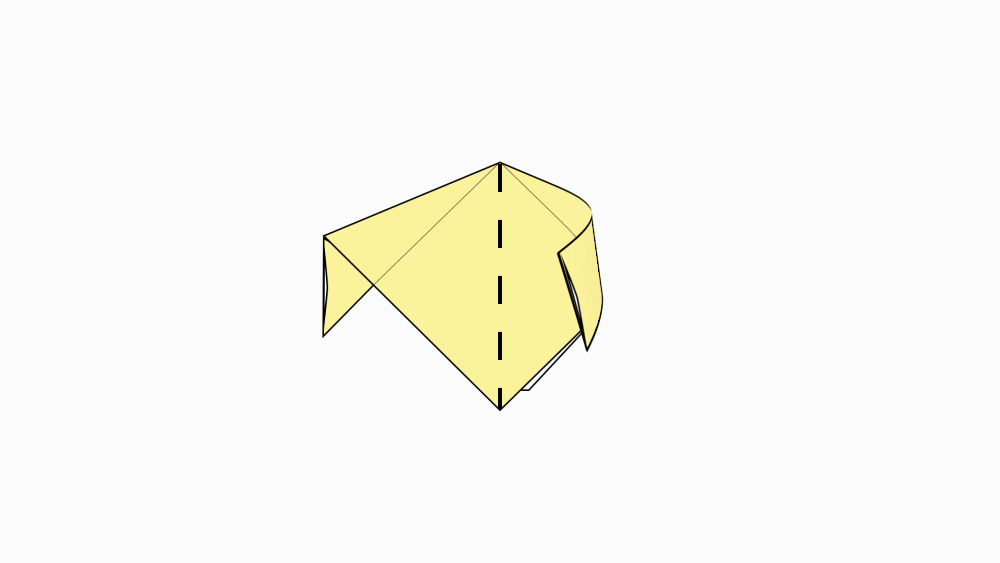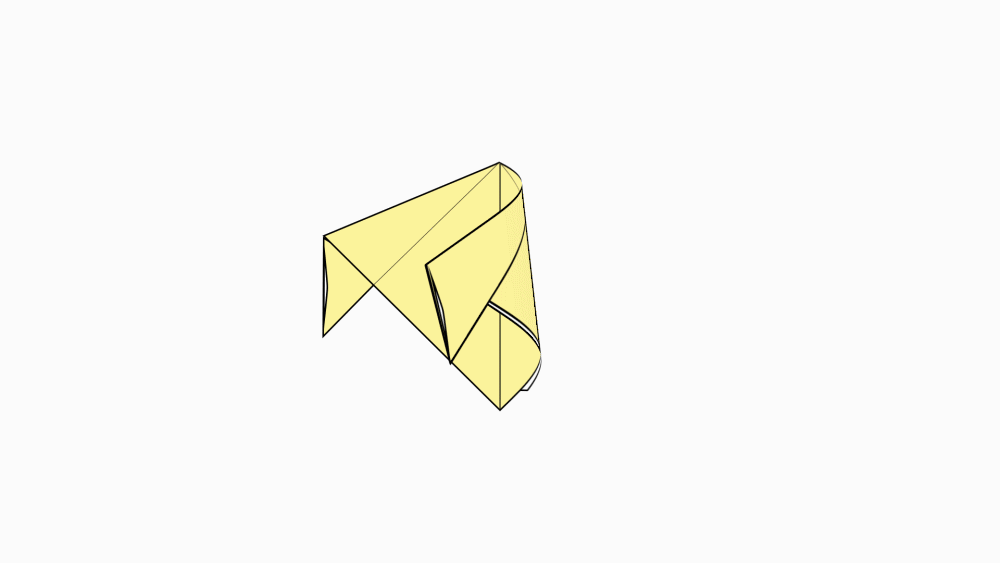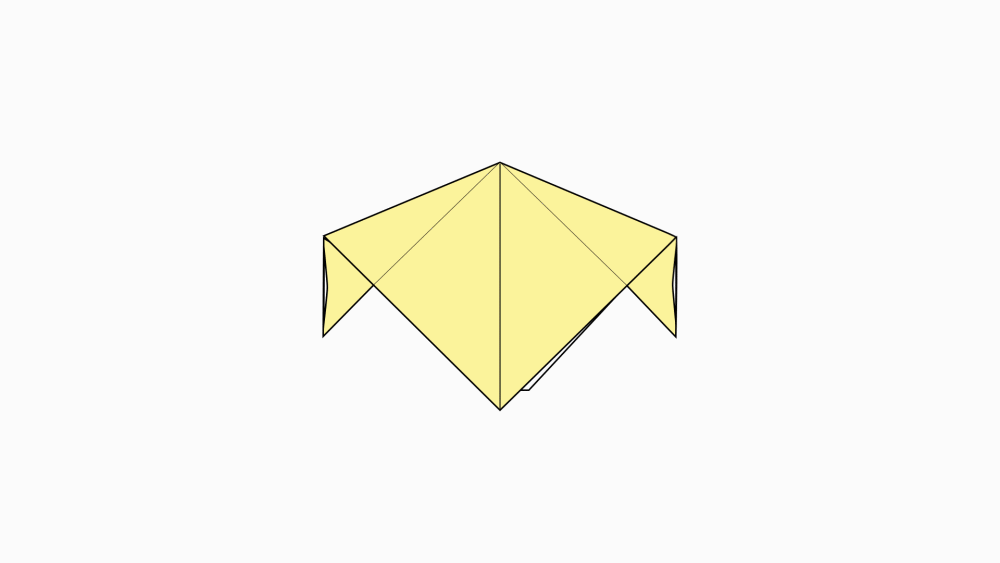
הוראת קיפול: לקפל ולפתוח.

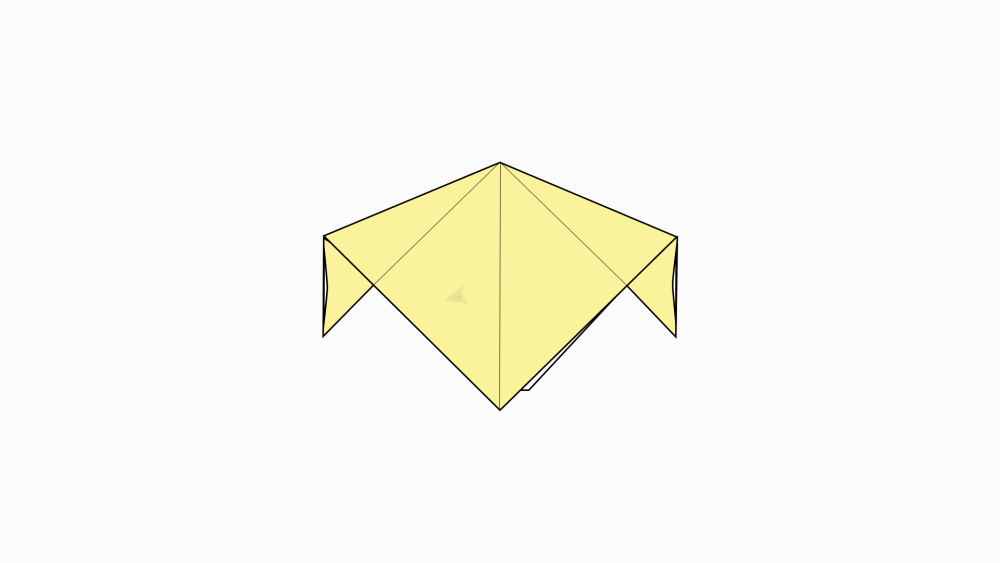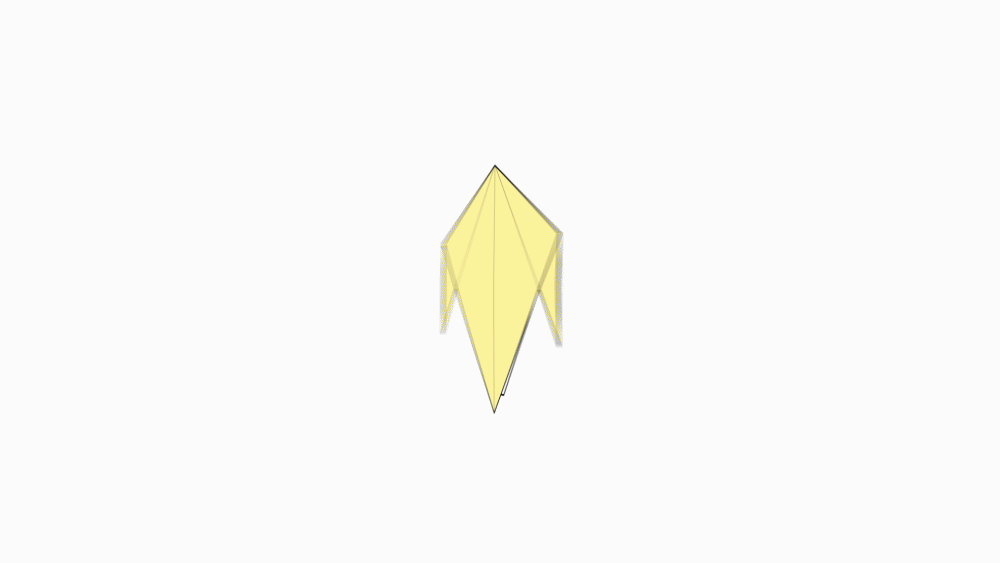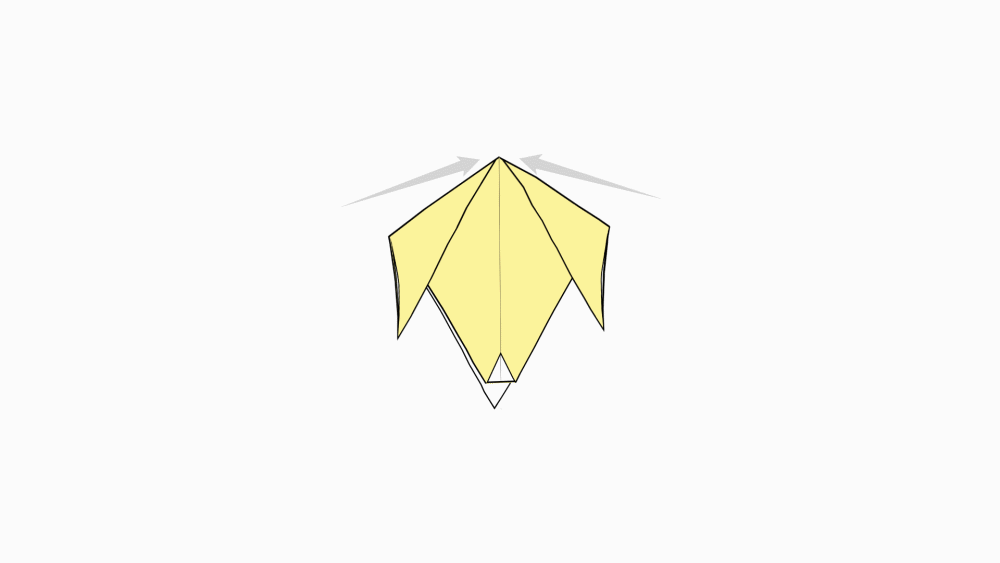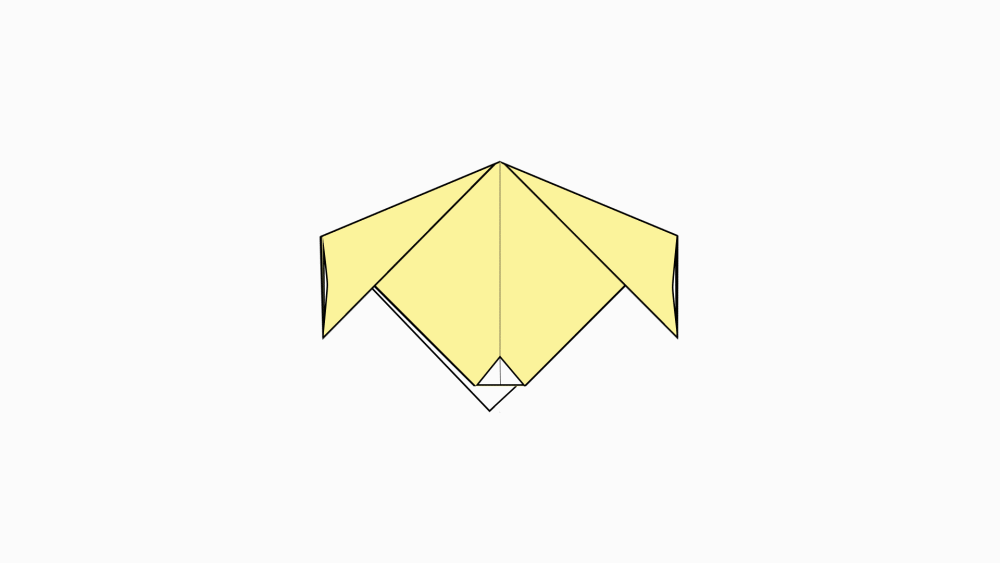
הוראת קיפול: להפוך לצד השני.

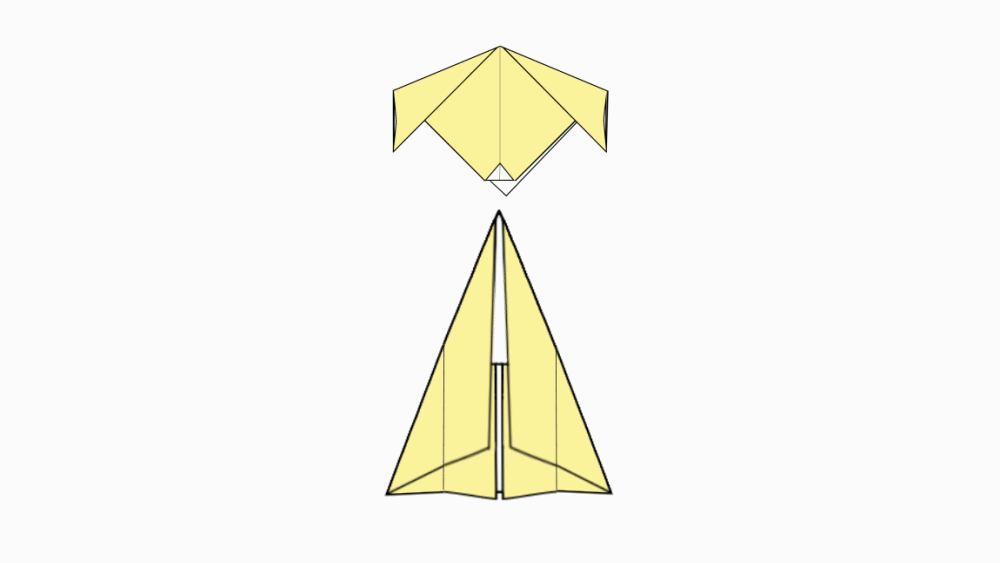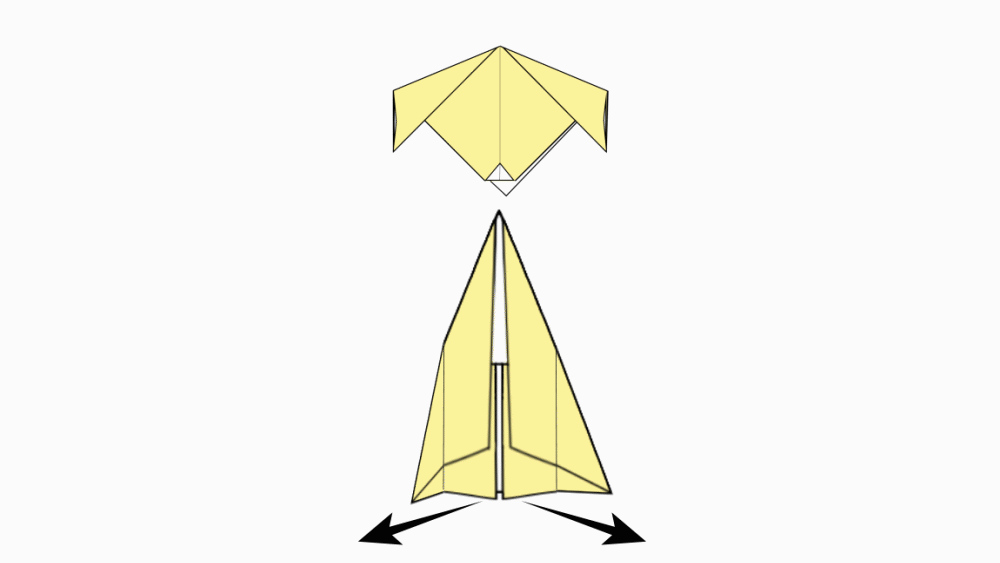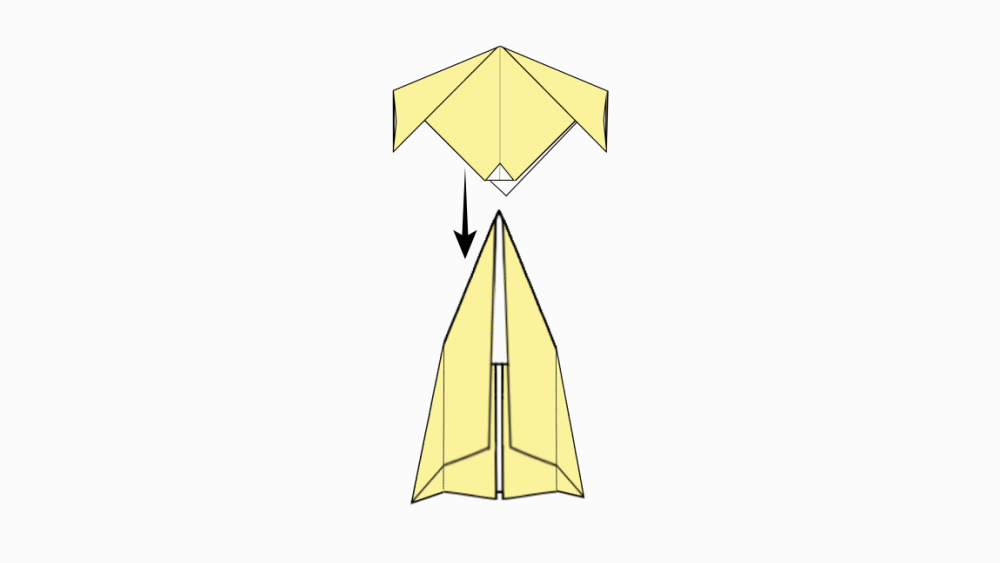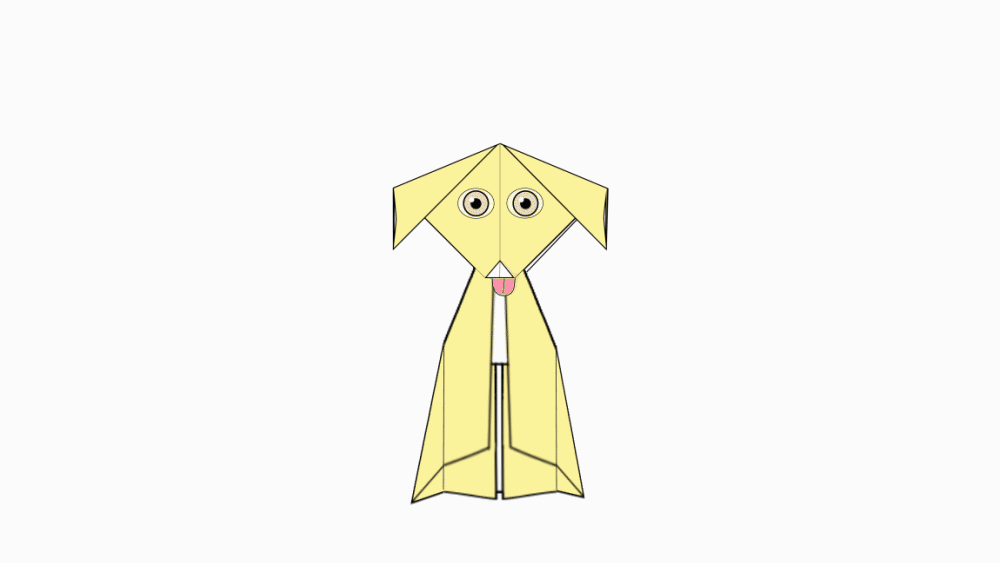
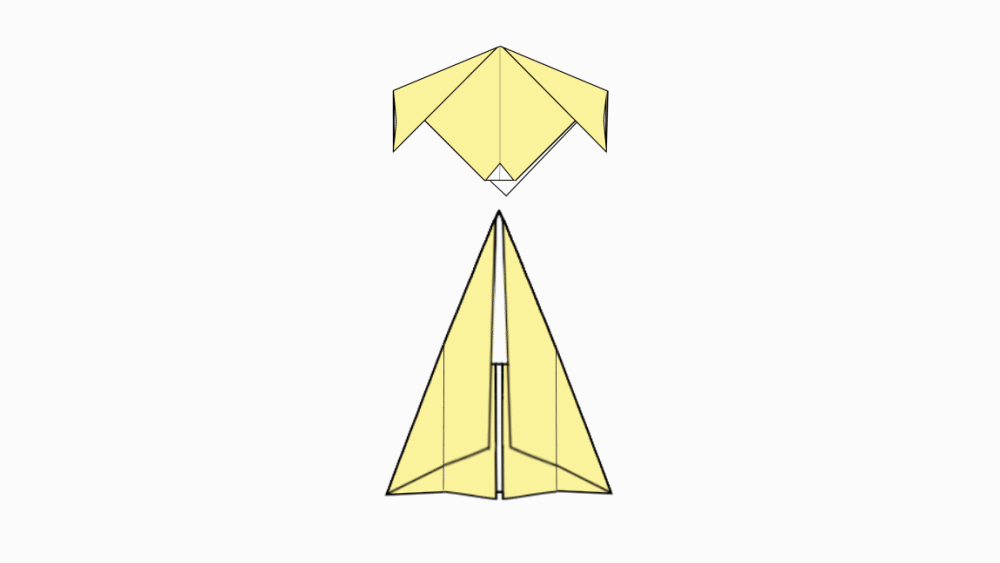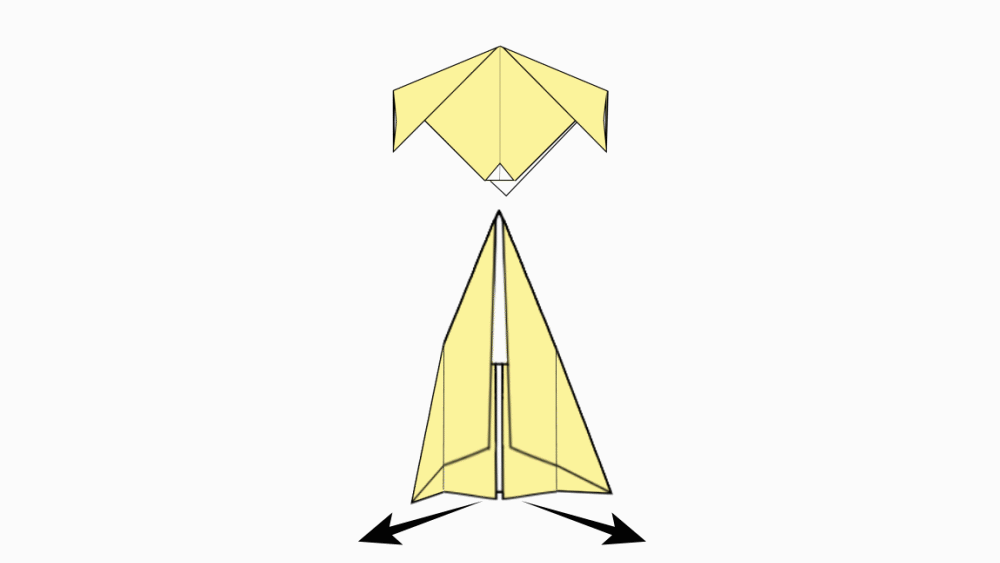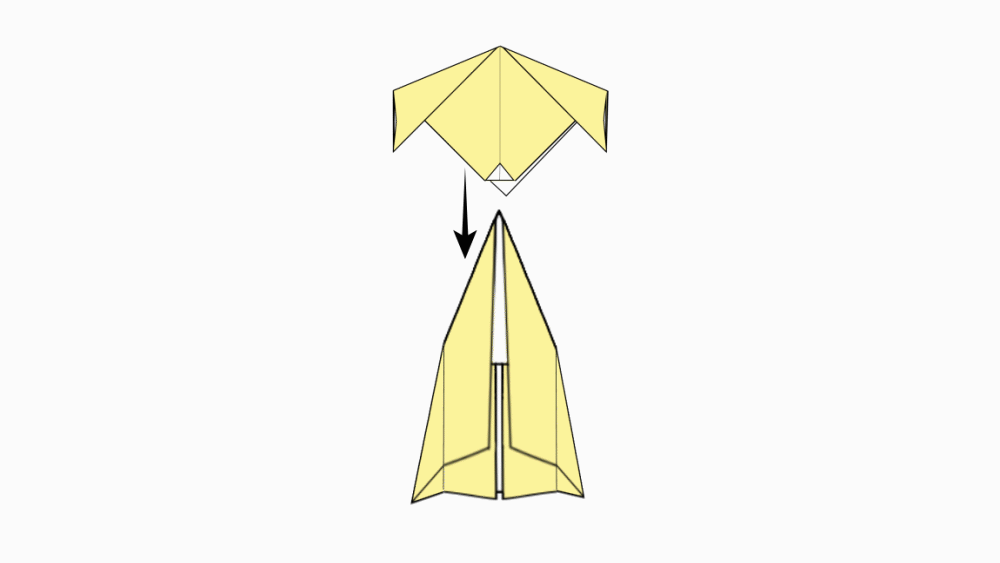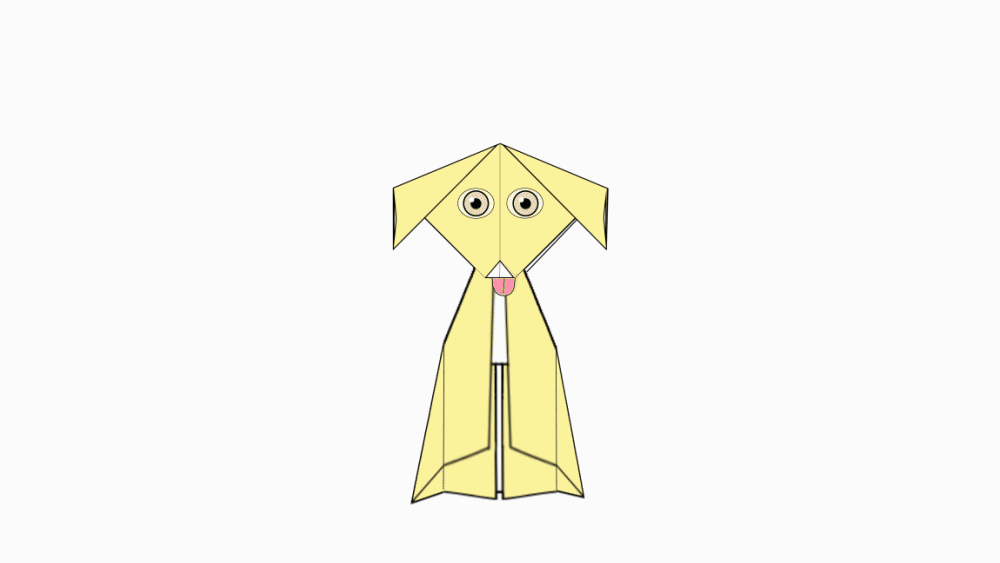
הוראת קיפול: נחבר את ראש הכלבלב אל הגוף.